Az arab számok eredetének kamu magyarázata: ne tessék neki bedőlni!
Évekkel ezelőtt kezdődött, de máig makacsul tatja magát az arabnak mondott számírás eredetét a vizuális jelek geometriájában felfedezni vélő magyarázat. A Facebookon terjedő megfejtés szerint (6 700 lájk, 19 323 megosztás) „az arab számok kinézete nem véletlenül lett kiválasztva”, hanem úgy, hogy az egyes számok „szögeinek” száma megegyezik a szám értékével.
Vagyis az elmélet szerint az 1-es számban egy „szög” található, a 2-esben kettő, és így tovább, bár ahhoz már elég sok kreatív energia kell, hogy valaki a 9-esbe belelássa a 9 szöget, a külső és belső szögekkel való trükközésről nem is beszélve:
Nem minden arab, ami annak látszik
Kezdjük az elején: az arab számjegyek valójában nem „kiválasztva lettek”, hanem az évszádaok során kialakultak, ráadásul nem az araboknál, hanem Indiában, és az írásbeliség megjelenéséhez képest későn. A sok ezer éves babiloni, sumer, görög és római numerikus leképezés-változatok után a forradalmi változást a számok helyi érték alapú lejegyzése jelentette.
Az 1881-ben megtalált, sáradá írással, gáthá dialektusban, nyírfakéregre íródott, valószínűsíthetően az időszámítás utáni 2-3. században keletkezett bakhsáli kézirat a legrégebbi forrás. A töredékes mű az alapvető aritmetikai témákat (többek közt a nullát, a törteket és a műveleteket) taglalta – tízes alapú helyi értékes számábrázolással. Így:
Az indiai számokat és használatukat az időszámítás utáni 780-ba született perzsa származású Abu Abdalláh Muhammad ibn Músza al-Hvárizmi avatta arabbá.
Bagdadban jelent meg a Számítás hindu számokkal című munka a 9. század elején. Szerzője, al-Hvárazmi alkotta meg az algebra és az algoritmus szavakat is, sőt a zéró szó is arab eredetű, a صفر ṣifr, üres olasz változata honosult meg különböző módokon az európai nyelvekben. (Az arab kifejezés a szanszkrit sunya fordítása.)
Fibonacci és Dürer – szög nélkül
A hindu-arab számokként is ismert jelöléseknek három fontosabb változata létezik ma is: az indiai, a keleti arab és a nyugati arab. Európába a legutóbbi érkezett el, a 976-os Codex Vigilanusban szerepel először.
A számolni Észak-Afrikában tanuló talján Leonardo Fibonacci 1202-ben kiadott Liber Abaciban már ezt az írásképet használta, de a meggyökeresedéséhez szükség volt a nyomtatás elterjedésére: Angliában például Gutenberg első, 1439-re datált nyomdakísérlete után néhány évvel, 1445-ben, Magyarországon bő tíz évvel később, Oroszországban viszont csak Nagy Péter regnálása alatt, a 18. század végén, Kínában és Japánban pedig még száz évvel később kezdték használni a ma arabnak nevezett számjegyeket.
Dél-Ázsia és Délkelet-Ázsia bizonyos nyelvei a bráhmi családba tartozó saját írásmódot használnak. Ilyen például a burmai, a thai, a lao, és a khmer. Ezek a nyelvek nem csak bráhmi írásra visszavezethető írásjelekkel rendelkeznek, de többségüknek saját, a hindu-arabhoz hasonló, helyiérték-alapú számjegyeik is vannak. Ugyan ma már az európai számjegyek is általánosan ismertek ezeken a területeken, de a hagyományos helyi számjegyek használta is él még. Egyiptomtól nyugatra az Európában is ismert nyugati arab számjegyek jellemzőek, a többi területen viszont a keleti arab számjegyek az általánosan elterjedtek.
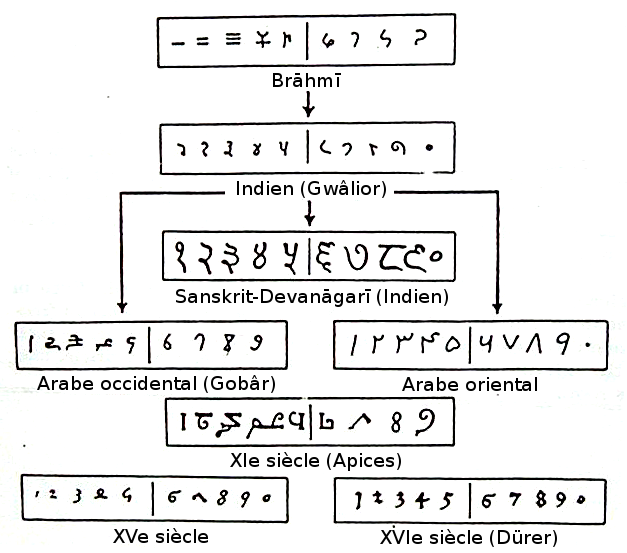
A ma használatos számok írásképét a tipográfiatörténészek szerint a 15-16- századi német festő, Albrecht Dürer alkotta meg. Az ő 1514-es Melankólia (I.) című metszetén azonban főleg lekerekített, szögletmentes formák láthatók, vagyis az sem igaz, hogy Dürer alakította volna úgy a számokat, hogy azok annyi „szögből” álljanak, amilyen értéket jeleznek.
Tudományos tévtanokról korábban így írtunk: