Előző heti feladványunkban nyolc egyforma fenyőfát kellett a hatágú csillagba szuszakolni, most kilencet kellene, de a száruk eltérő hosszúságú.

107. feladvány: Karácsonyi szuszakolás másodszor

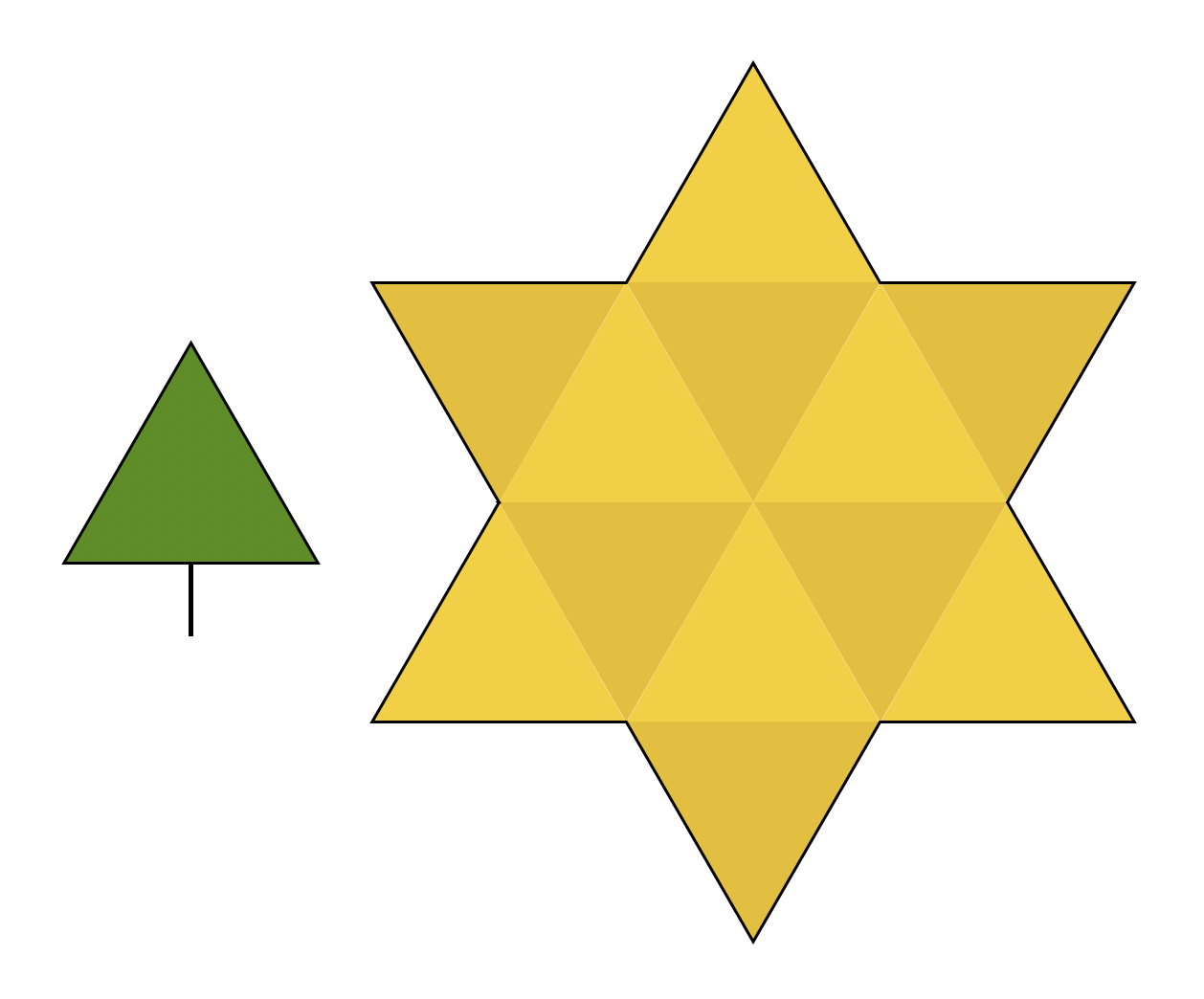
Az alábbi ábrán látható háromszögek mind szabályosak, azaz minden oldaluk egyforma hosszú. Az aranyszínű háromszögekből álló, csillag alakú területre kilenc darab fenyőfát kellene beszuszakolni, amelyek lombkoronája szintén ugyanakkora szabályos háromszög, mint az aranyszínű háromszögek. A fenyőfáknak azonban száruk is van, amik nem lóghatnak bele más fa koronájába, és a szárak sem keresztezhetik egymást.

Minden fenyő szára merőleges a lombkoronáját alkotó háromszög alsó oldalára, és annak felezőpontjából indul. Egy fenyő teljes magassága tehát a szár hosszából és a háromszög magasságából áll össze. A fenyő szélessége a szabályos háromszög oldalhossza. A fák lombkoronái egyformák, a száruk azonban különböző hosszúságú. A fenyők magasságai rendre: 96, 97, 98, 99, 100, 101, 102, 103 és 104 cm. A fenyőket tetszőlegesen szabad forgatni, de nem fedhetik át egymást, sem a koronájuk, sem a száruk. A szárukról feltehetjük, hogy a vastagságuk elhanyagolható. Be lehet-e pakolni mind a kilenc fenyőfát a csillagba úgy, hogy sehol ne lógjanak ki?

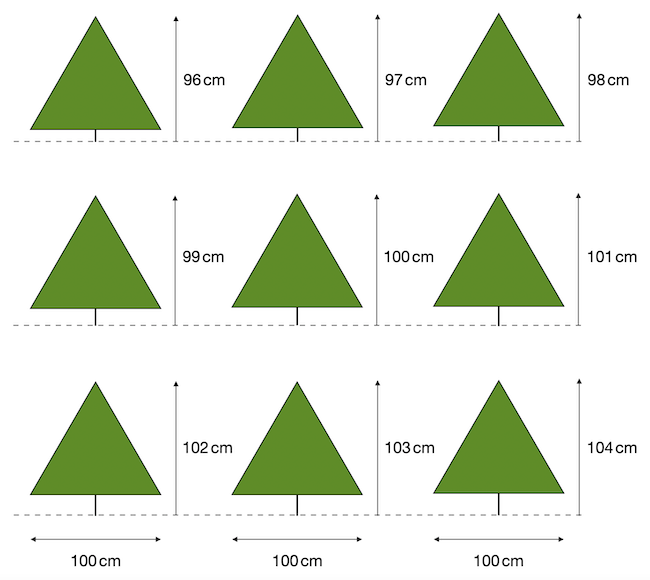
Bónusz feladvány, amely segítségnek is felfogható: hogyan lehet bepakolni kilenc egyforma fenyőfát a hatágú csillagba, ha a fák szélessége 100 cm, teljes magasságuk pedig 98 cm?

Nehézségi szint:

A megfejtéseket ábrával és részletes magyarázattal együtt az eszventura@qubit.hu címre várjuk. A legértékesebb megoldást küldő versenyzők felkerülnek az Ész Ventura dicsőségfalára, közöttük és minden jó megoldást beküldő versenyző között év végén nyereményeket sorsolunk ki. Az e-mail subject mezőjében kérjük sorszámmal jelezni, hogy melyik feladvány megoldásáról van szó. Beküldési határidő: január 5. éjfél.

Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus és bűvész.