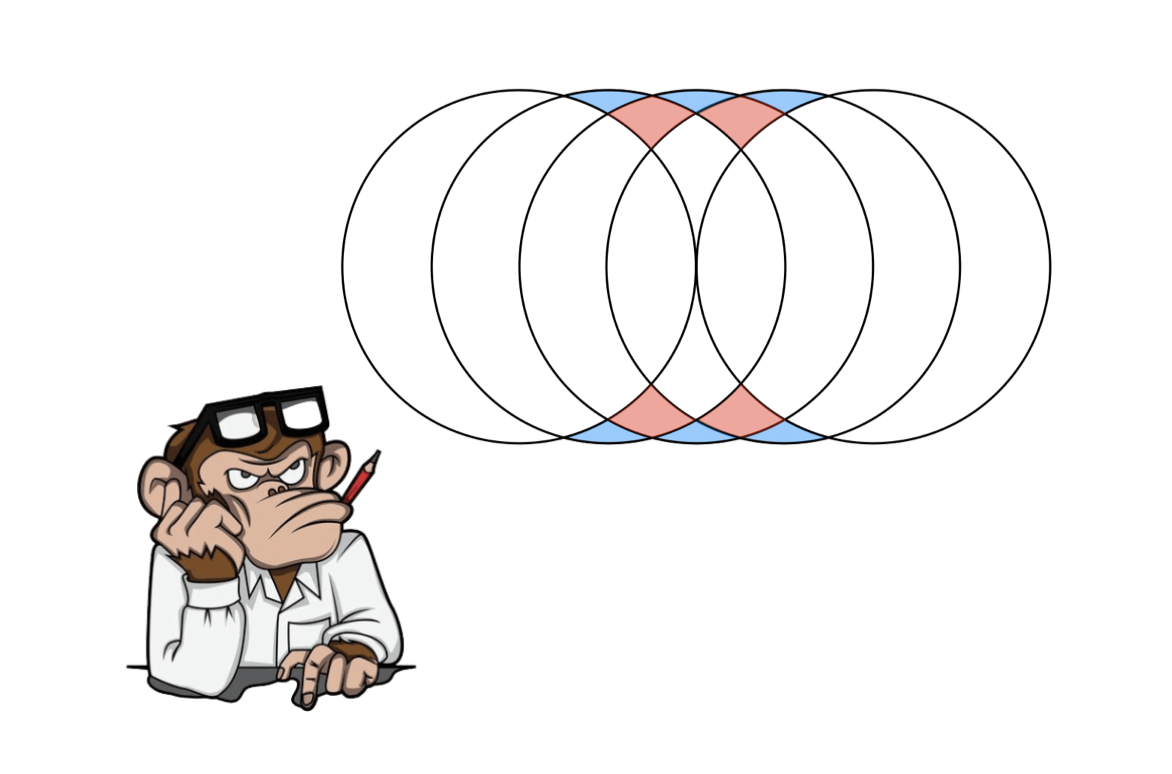
Melyik terület a nagyobb?
A pirosra vagy a kékre színezett terület a nagyobb?

A pirosra vagy a kékre színezett terület a nagyobb?

Mi a legrövidebb út, ahogy a katicabogár a magasba juthat, és ez mennyivel rövidebb annál, amikor a katicabogár úgy halad, hogy mindig lokálisan tör a legmagasabbra?

A mesterséges intelligenciáról szóló beszélgetésekben gyakran felbukkan az a várakozás, hogy a gépek majd racionálisabb döntéseket tudnak hozni, mint mi, mert optimalizálni tudják, amit kell. Nézzük meg közelebbről, miért nem olyan egyszerű ez, mint ahogy elsőre hangzik.

Hogy lehet az, hogy egy kétfős szerencsejátékban valaki nagyobb eséllyel nyer, mint a másik, mégsem nyerhet az esetek felénél többször?

Elhiszed, hogy ez a 2026 jegyű szám egy prímszám? Nagyságrendileg csupán tíz az ezrediken, azaz googol a tizediken prímosztót kellene kipróbálni, vagyis mindegyikre megnézni, hogy osztja-e a számot. Te viszont próbálj meg csak annyit belátni, hogy a következő három prím nem osztja: 13, 113 és 1013!

Hallottál már a nagy, jeges neutrínó detektorról? Ha nem, ismerkedj meg vele, majd válaszold meg a kérdést, hogy véletlen dátumokat véve mekkora a napot jelző számokban a különböző számjegyek valószínűsége!

Tegyük fel, hogy a magyarok úgy döntenek, közösen visszafizetik az államadósságot, hogy ne örökítsék ők is tovább a következő generációkra. Számold ki, te mennyi idő alatt tudnád törleszteni az adósságodat!

Fejtsd meg a kódot, és megtudhatod, hogy milyen különlegesség van még a New Horizons űrszonda fedélzetén az ott lévő műszereken kívül!

Ugye te jobban gazdálkodtál volna a pontjaiddal?
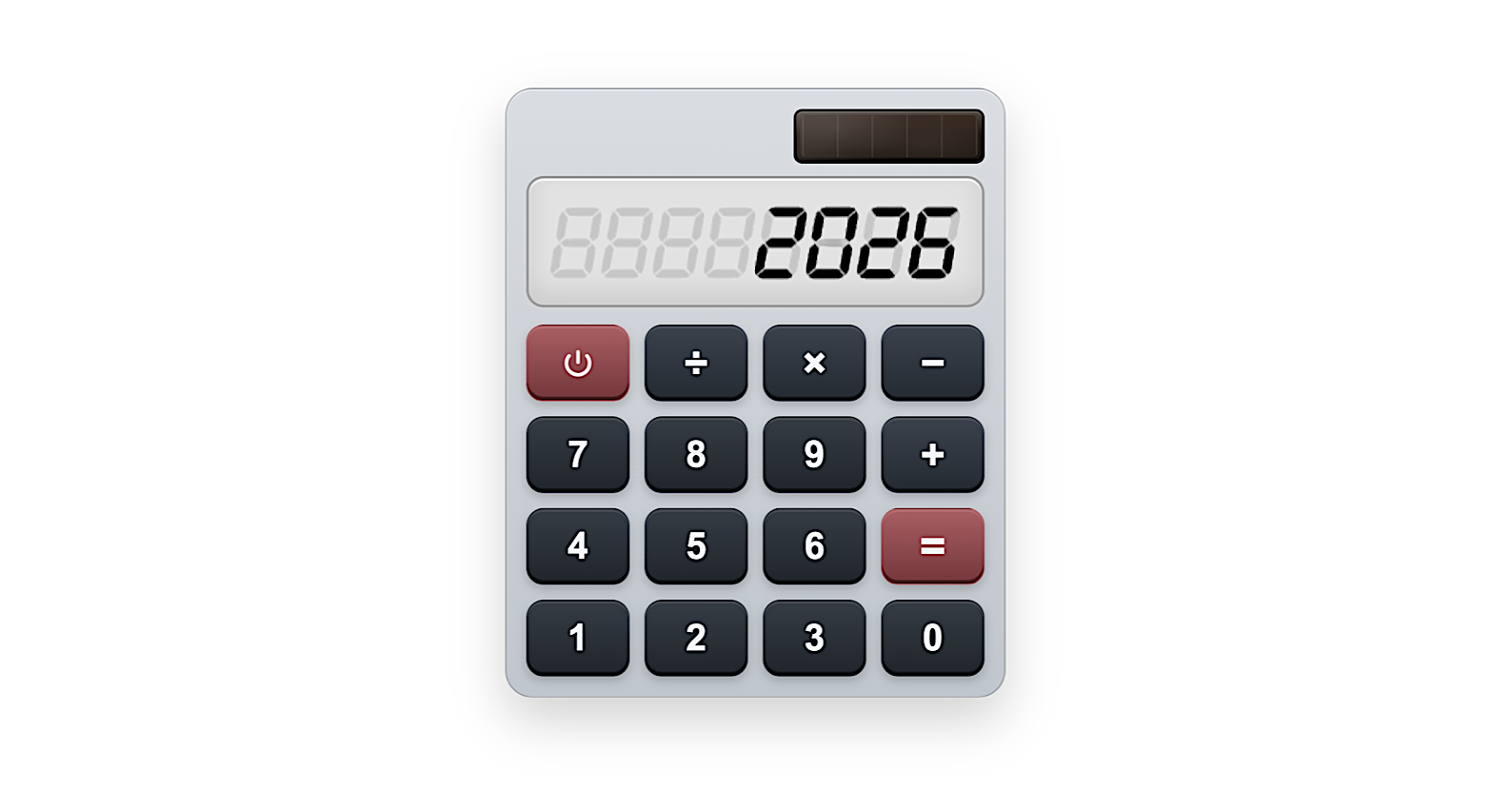
A gépen lévő gombok: a számjegyek 0-tól 9-ig és a négy alapművelet, továbbá az egyenlőségjel, amit a legvégén kell megnyomni.
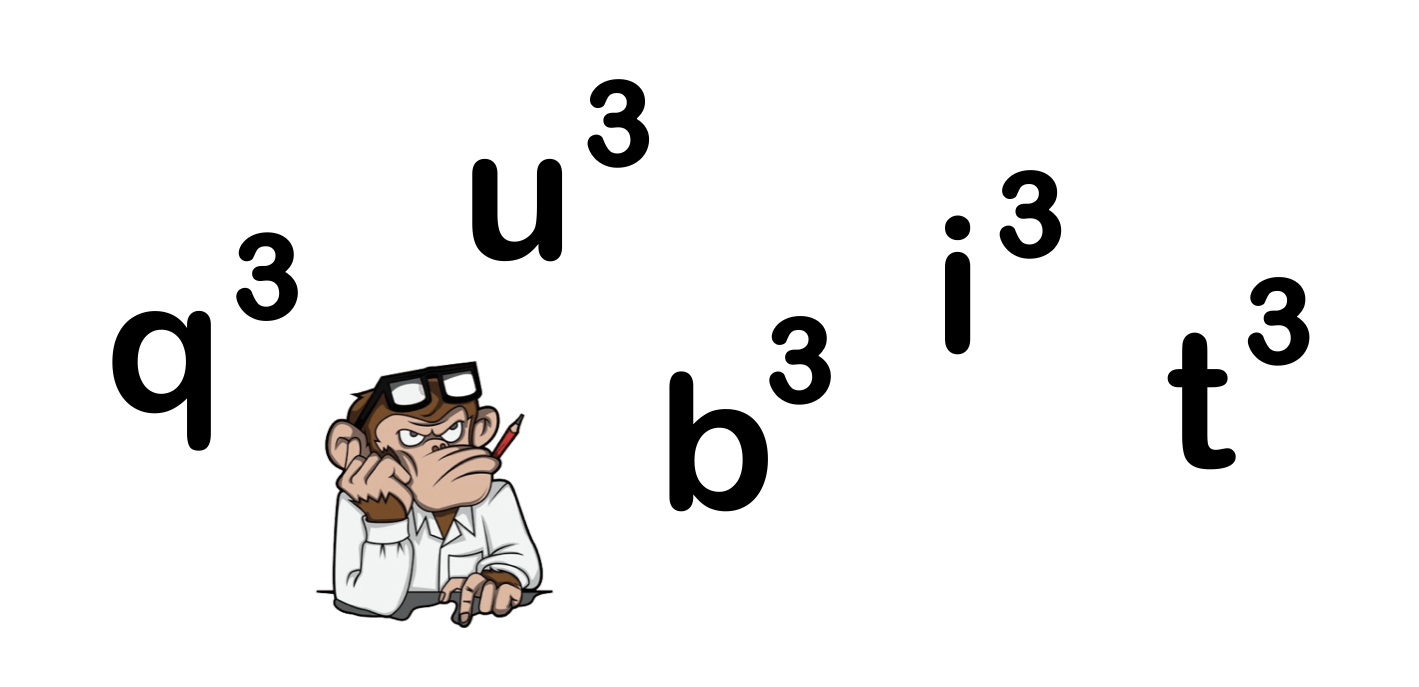
A 2025-ös év több szempontból is különleges volt – elég, ha csak az évszámot nézzük.
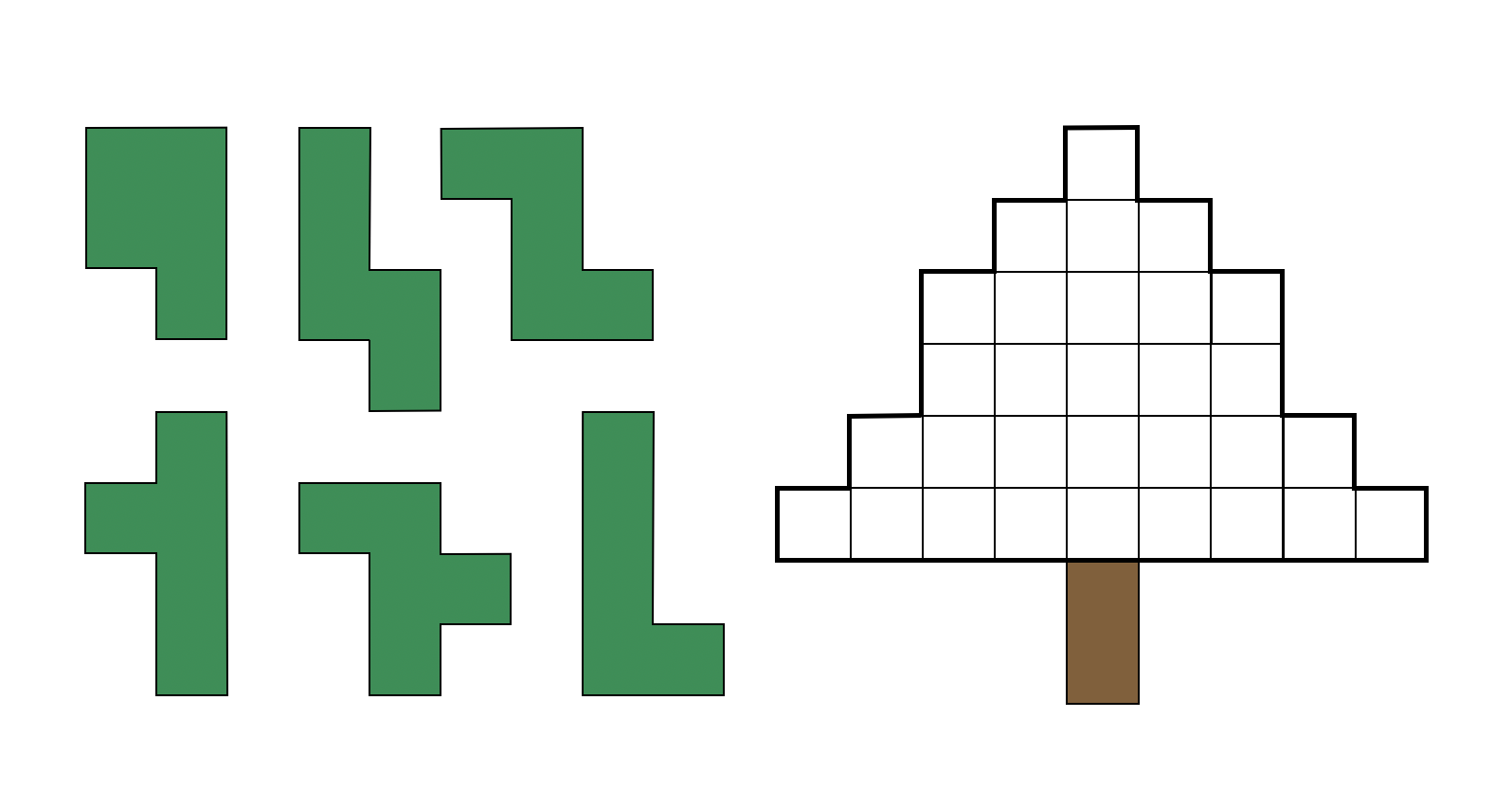
Meg tudod oldani a karácsonyi feladványt még karácsony előtt?
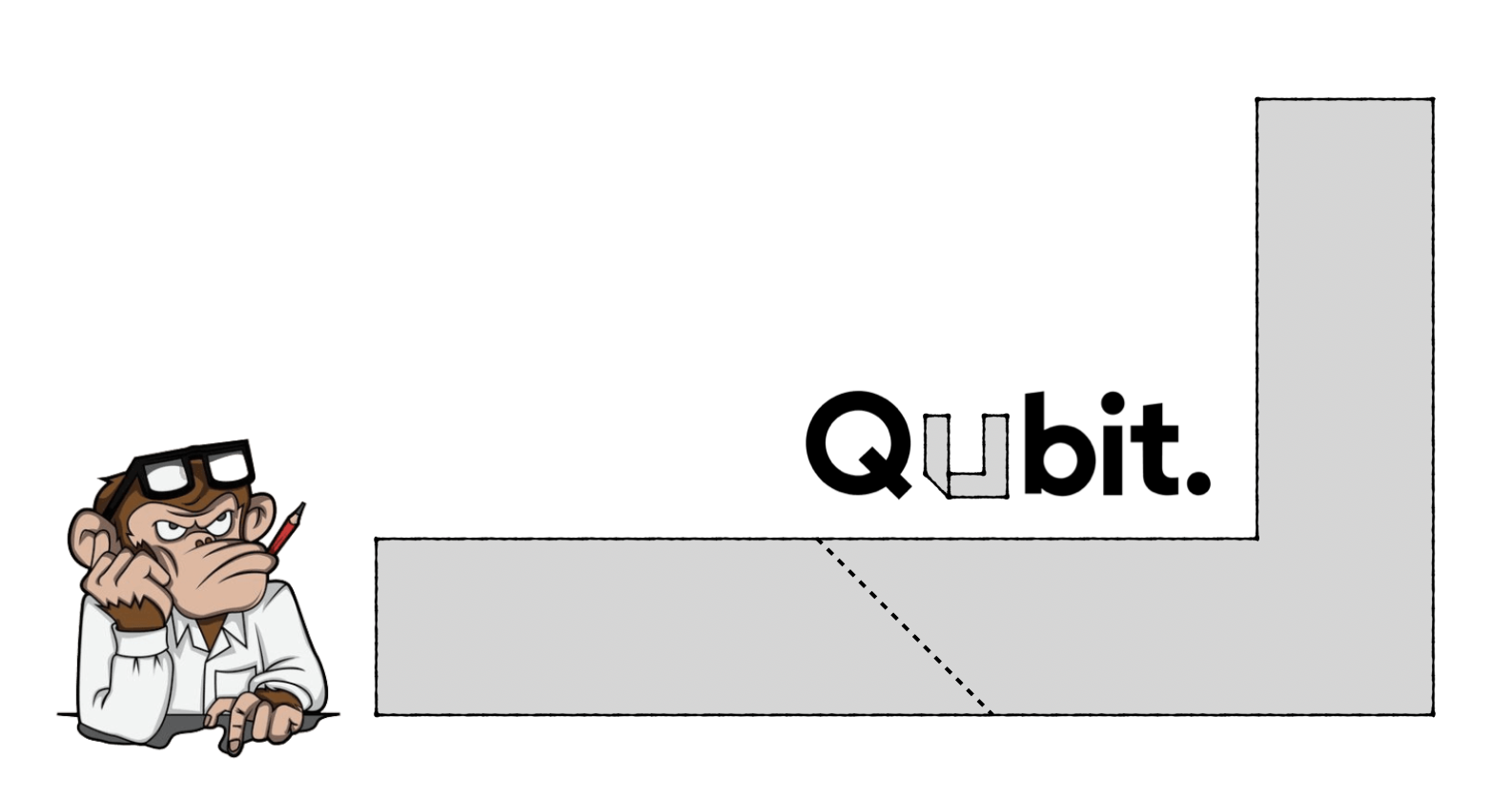
Valaki kartonpapírból kivágott egy betűt, majd egyetlen hajtást végzett rajta. Milyen kis- és nagybetűk jöhetnek szóba?

Ezen a héten különleges feladvánnyal jelentkezünk, amelynek alapját a ChatGPT találta ki. Ő nem boldogult vele, ti meg tudjátok oldani?
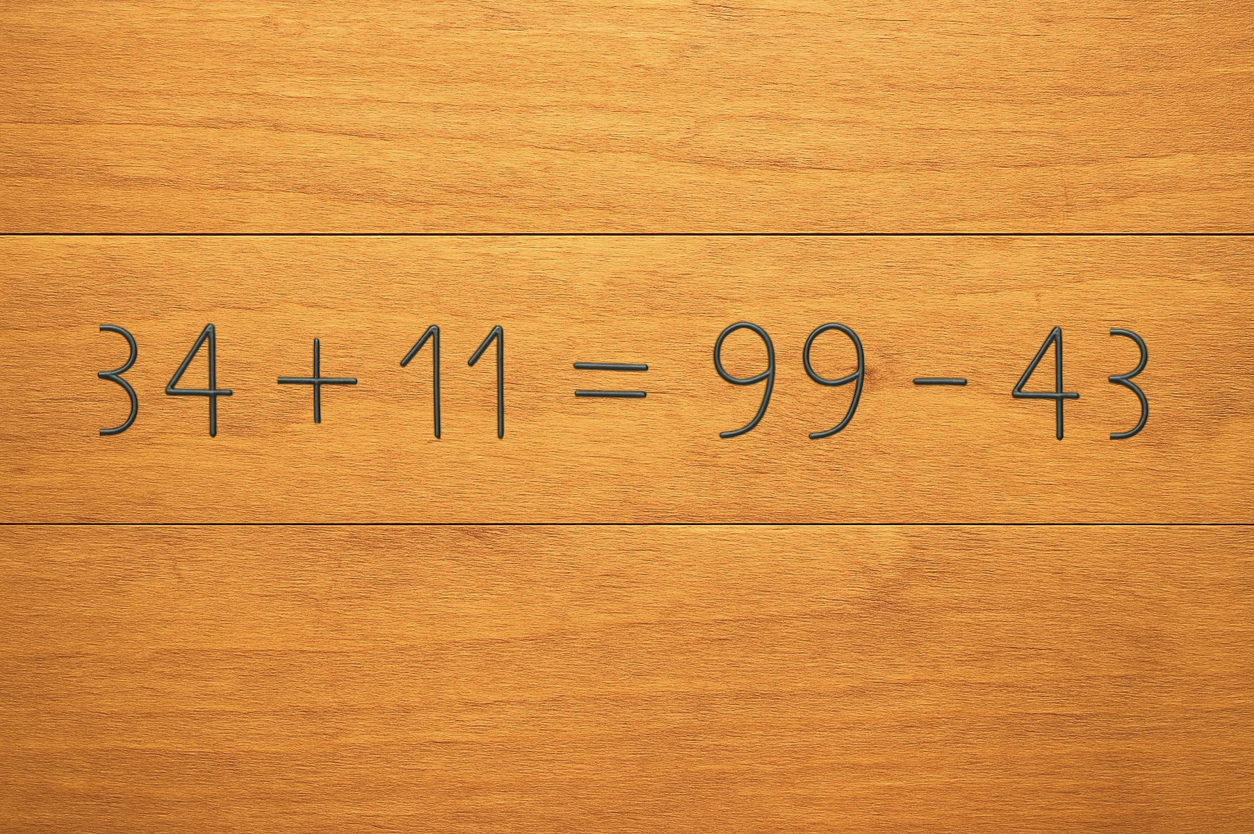
Egyetlen drótból készült alakzat (például egy számjegy) áthelyezésével tedd igazzá az egyenlőséget!