Gravitrax körút című feladványunkban az volt a kérdés, hogy a Gravitrax hatszögletű alapelemeinek (lásd az alábbi ábrán jobb oldalt) felhasználásával lehetséges-e egy körutat (önmagába visszatérő utat) építeni a Gravitrax táblájára (lásd az alábbi ábrán bal oldalt) úgy, hogy a tábla minden mezőjére teszünk elemet, és minden felhelyezett elem része is a körútnak, azaz legyen rajta legalább egy ív, ami a körút része. Az elemeket szabad forgatni, de nem lehet tükrözni!

Egy kis kísérletezés után sejthetjük, hogy akárhogy is próbáljuk kitölteni a táblát, legalább egy mező mindig kimarad a körútból. Alább láthatunk néhány próbálkozást, de az, hogy nem sikerül, nem jelenti azt, hogy biztosan nem lehetséges. Hogyan lehetne bizonyítani?

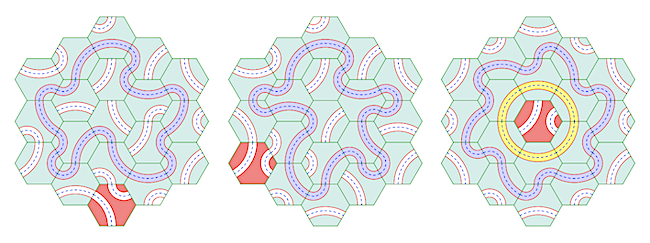
Nézzük a tábla sarkait. A fenti példák alapján is látható, hogy a sarkok vagy kimaradtak, vagy forgásszimmetrikus lett az ábra, és a sarkokban lévő elemek mindenhol a kis kanyarral vesznek részt a körútban. Próbáljuk elsőként ennek a szükségességét bizonyítani.

Nézzük a tábla egyik oldalát, ami két sarokból és a köztük lévő oldalsó elemből áll, lásd narancs és piros mezők az alábbi illusztráción. Bármely elemet vizsgáljuk azon kell lennie egy körút darabnak, aminek két vége van, azaz a körút két szomszédos mezővel áll kapcsolatban. Nézzük, honnan futhat be a körút a piros mezőre. Mindkét narancs mezőről nem futhat be, mert akkor a piros mezőre vagy egy egyenes kellene az összekötésükhöz, vagy két kis kanyar, hogy mindkettő elkanyarodjon valamelyik sötétszürke belső mező felé, de a felhasználható elemen se szemközti oldalakat összekötő egyenes út nincs, sem pedig két kis kanyar. Megállapíthatjuk tehát, hogy egy ilyen piros mezőre vagy csak az egyik narancssárgából mehet körút, vagy egyikből se. Igen ám, de minden sarkos mezőről legalább egy út mindenképpen vezet a sarkok között lévő oldalsó mezők egyikére, viszont a korábbiak miatt tudjuk, hogy összesen legfeljebb hat, így ki lehet zárni a nagy kanyarokat a sarkokban, mivel egy nagy kanyar esetén már legalább hét út vezetne összesen az oldalsó mezőkre.

Továbbá ezeknek a kis kanyaroknak minden sarkos mezőnek ugyanazon az oldalán kell elhelyezkedniük a tábla középpontjából nézve, mert ha ezek az utak nem vezetnének ugyanabba az irányba, akkor kellene lennie egy olyan résznek, ahol szembe mennek, azaz egy oldalsó (piros) mezőre két sarkos (narancs) irányból is érkezik út, de azt már megállapítottuk, hogy ez nem lehet. A sarkos mezők tehát vagy úgy vannak, ahogyan a fenti ábrán látható három próbálkozásból a jobb szélsőn, vagy annak tükörképe jöhet még szóba.

Nézzük előbb az első esetet, amin belül két eset lehetséges. Vagy mindegyik oldalsó (piros) mező kis kanyarral vesz részt a körútban, vagy van legalább egy, amelyik nagy ívvel. Ha kis kanyarral vesznek részt, akkor egyértelmű a folytatás befelé, figyelembe véve, hogy három kis körívből álló hurkokat nem csinálhatunk, mert az különálló körút lenne. Ha viszont mindenhol egyértelműen kiegészítjük az eddigieket, akkor egy olyan körút áll össze, amiből a tábla középső mezője kimarad.

Ha van legalább egy nagyméretű kanyar valamelyik oldalsó (piros) mezőn, akkor ennek folytatásában létrejön egy olyan mező, ahová már két út is vezet. Ha megvizsgáljuk, erre a mezőre kétféle módon is lerakhatjuk az alapelemet: vagy rögtön visszakötjük a következő sarokhoz a körutat, vagy befelé folytatjuk. Ez utóbbi esetben könnyen belátható, hogy a következő sarok szomszédsága nem folytatható, ha viszont mindenhol továbbkötjük a sarokhoz, akkor a végén körbeérünk, és megint kimarad a tábla középső mezője.

Nézzük most azt az esetet, amikor a sarkokon a kis ívek fordítva mennek, azaz a korábbinak tükrözöttje a minta. Ebben az esetben könnyen belátható, hogy ha bármelyik oldalsó (piros) mező kis kanyarral venne részt a körútban, akkor pár lépésen belül nem lehetne folytatni az építkezést. Ha viszont minden oldalsónál nagy ívet használunk, akkor megint egy olyan körút áll össze, amelyből kimarad a tábla középső mezője.

Érdekesség, hogy nagyobb táblán már lenne megoldás, Mérvadó Béla megoldónk mutat alább egy példát ilyen körútra.