Te ki tudod logikázni, milyen számok érintik az asztalt? A dobókockákról tudjuk, hogy egyformák, de nem feltétlenül szabványosak: minden oldalukon hagyományos elrendezésben vannak a pöttyök, de a szemközti számok összege nem biztos, hogy hét.
Egy feledékeny matematikusnak két egyforma kinézetű gyógyszert kell szednie felváltva. Milyen algoritmus szerint vegyen ki pirulákat a két félvégtelen bliszterből úgy, hogy a bliszterekre ránézve még a hét napjait is számon tudja tartani?
A franciák néggyel több bábuval játszák, mint az angolok, mi az?
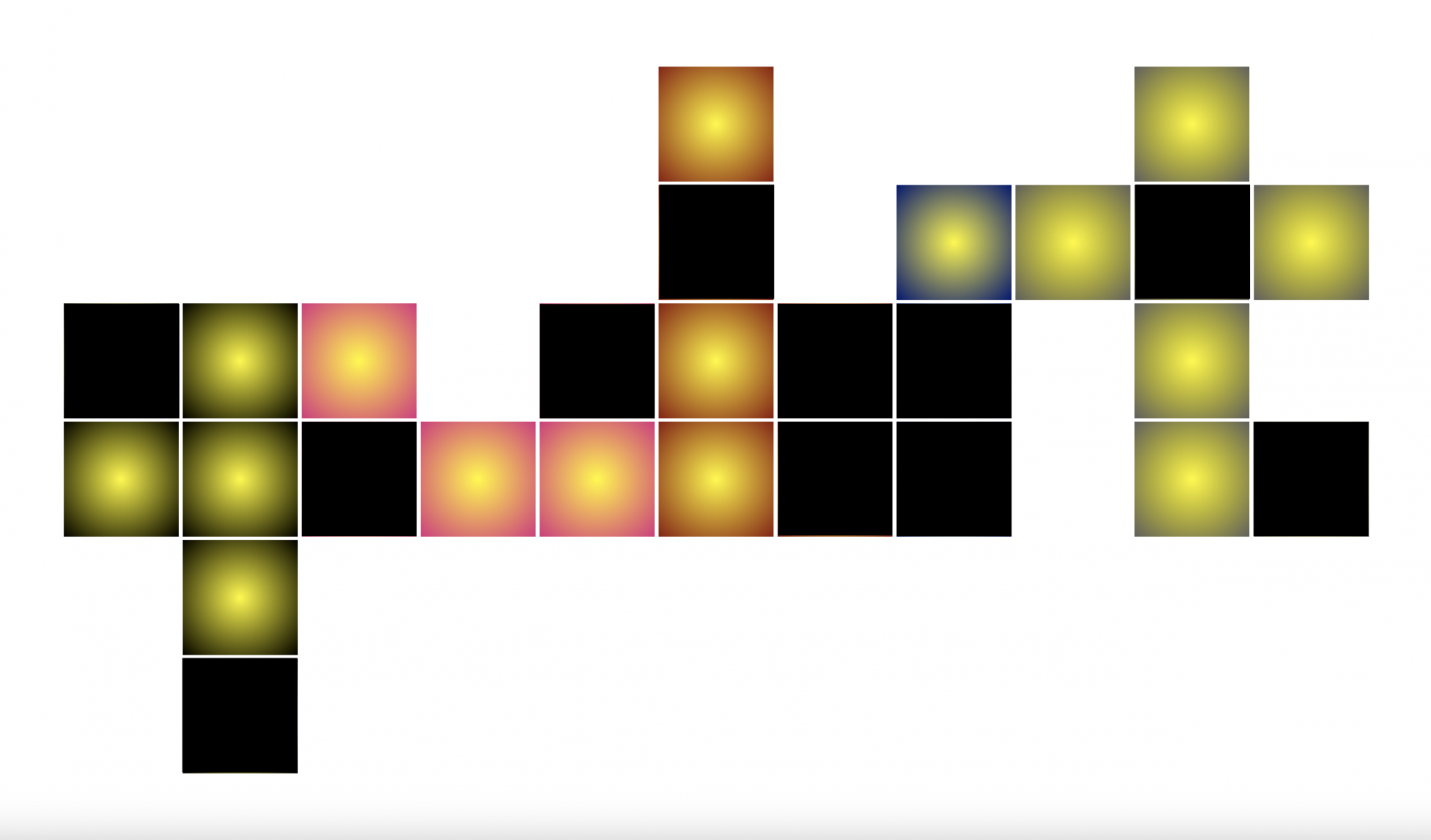
Feladványunkban lámpákat kellett kapcsolgatni úgy, hogy minden kapcsolásra a szomszédos szobában is átvált a lámpa.
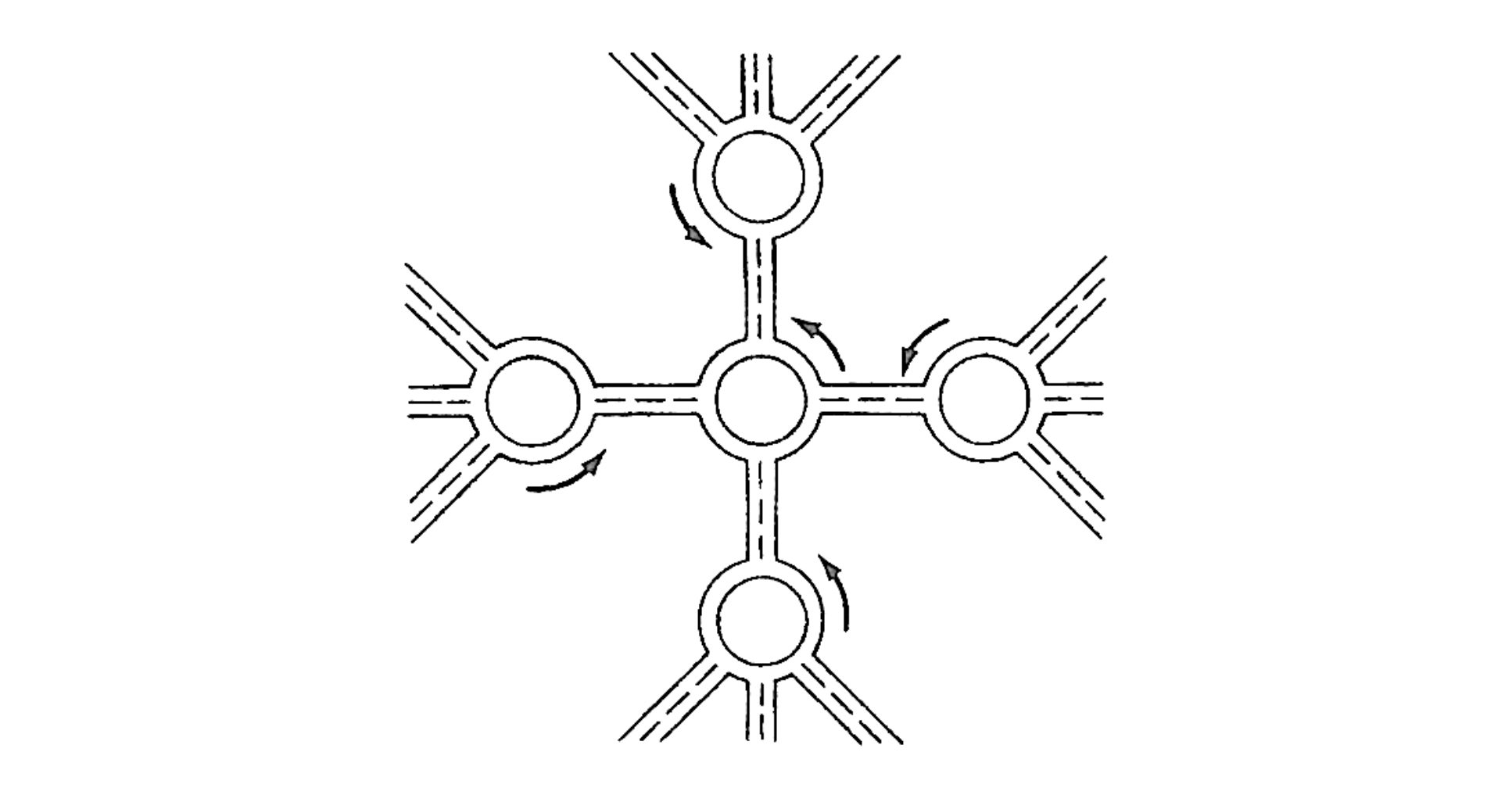
Körforgalom-tervező feladványunk megfejtőinek az ütközésveszély és a szédülésveszély között kellett egyensúlyozniuk. De sikerült?
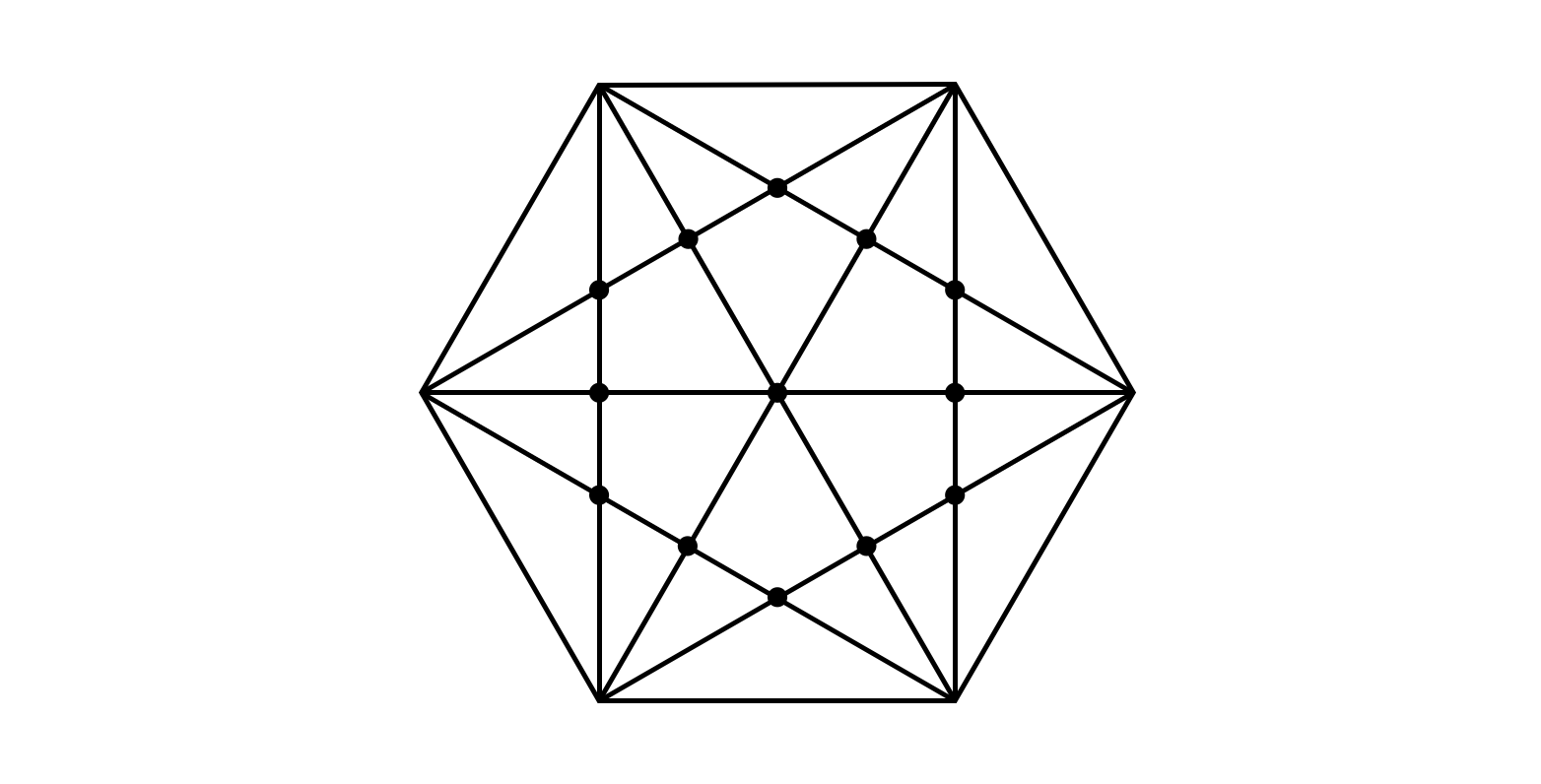
Te sem gondoltad végig? Pedig nem volt nehéz!
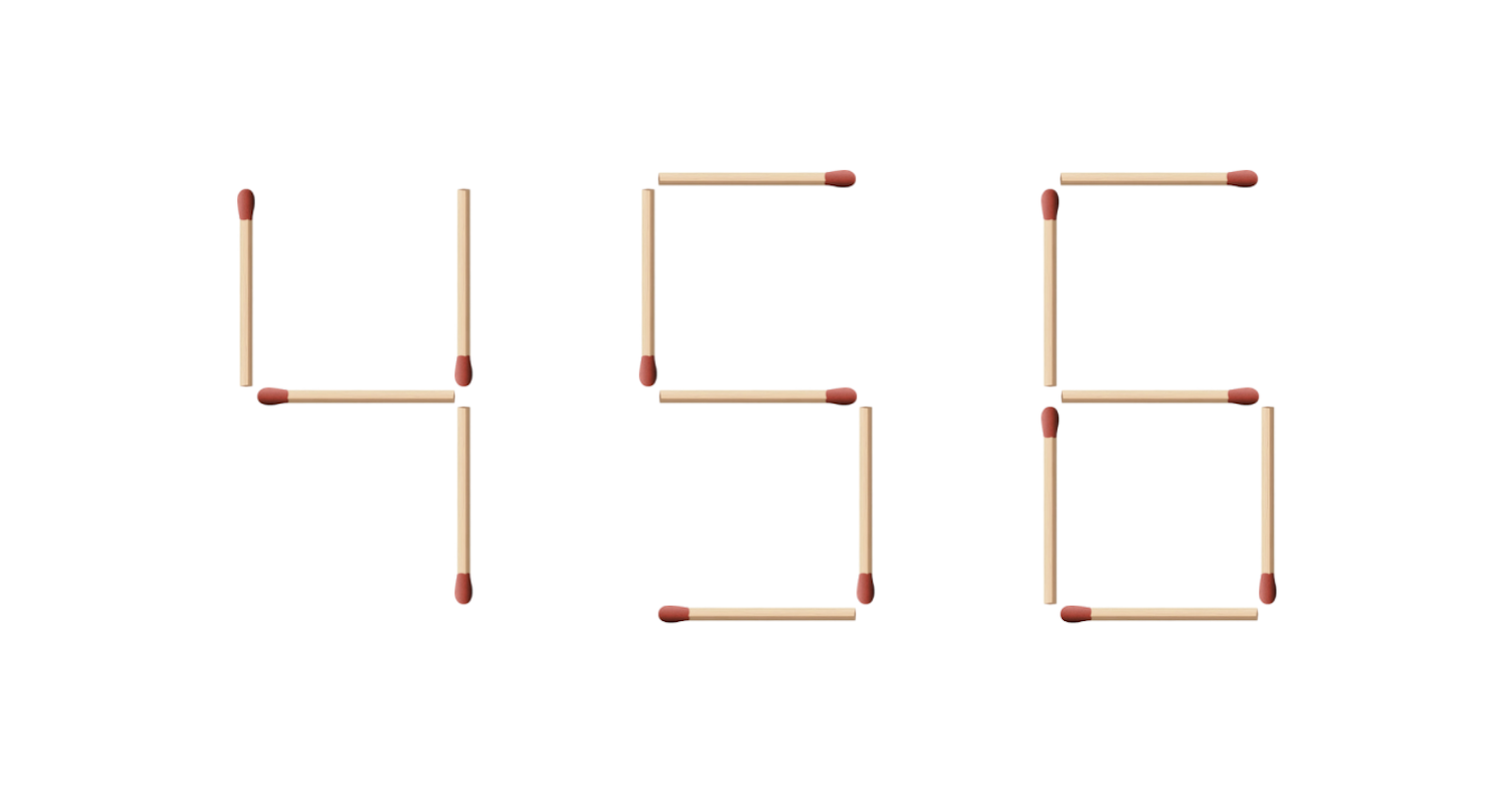
Egy gyufaszál áthelyezésével kellett négyzetszámot készíteni. Neked sikerült?
Két játékos felváltva veszi le a bábukat. A kérdés az volt, hogy melyikük tud biztosan nyerni, és milyen stratégiával.
Feladványunkban hajtogatott és lelapított papírcsomókból kellett megépíteni egy gömböt – most megmutatjuk, hogyan volt érdemes nekifogni.
Lehetett gondolkodni különböző trükkös megoldásokon, de ezúttal úgy néz ki, hogy a legegyszerűbb megoldás volt a legjobb.
Feladványunkban egy minden irányban végtelen négyzetrácsot kellett megtölteni négyféle sakkbábuval úgy, hogy mindegyik üssön legalább egyet minden másfajta bábuból, de ne üssön egyet se a saját fajtájából.
Feladványunkban azt kellett kiszámítani, hányan jutnak biztosan pokolra, ha tudjuk, hogy az emberek hány százaléka esik bele a hét főbűn valamelyikébe.
Össze lehet-e öntögetni a bort a szódával pazarlás nélkül a megadott szabályokkal? Mutatunk egy megoldást.
184. feladványunkban azt a kérdést tettük fel, hogy egy racionálisan gondolkodó egyed ki tudja-e használni a többiek ösztönviselkedését.
A Qubit betűit felhasználva kellett kirakni egy 5x11-es lyukas téglalapot – itt a megoldás, de két bónusz feladvány is jár mellé!