Mekkora fejtörést tud okozni az idei év?

242. feladvány: Csak hatványozás
Hány különböző értékű szám állítható elő a 2025 számjegyeiből, mindegyiket pontosan egyszer használva, ha nem használhatunk műveleti jeleket, csak a hatványozást?
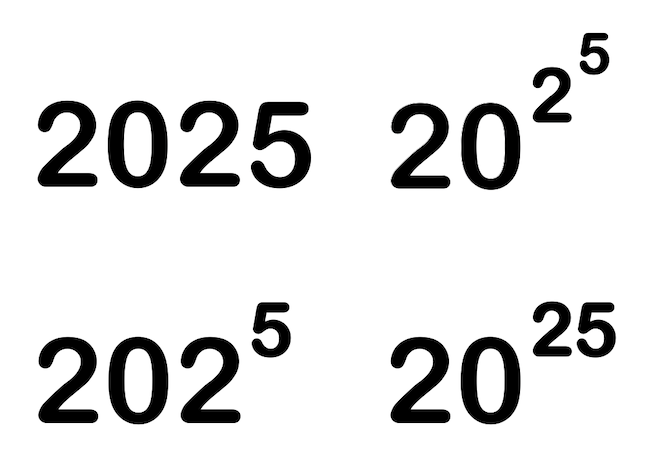
Tipp
Érdemes a torony szintjeinek száma, azaz a hatványozások száma és az alsó szinten lévő szám, azaz a hatványozás alapja szerint osztályozni a lehetőségeket, viszont figyeljünk arra, hogy különböző alakú számok is adhatják ugyanazt az eredményt.
Megoldás
Az első számjegy, amit leírunk, lehet háromféle: 0, 2 vagy 5. Ha az első számjegy 0, akkor minden más már csak kitevőben lehet, és az eredmény fixen 0 lesz. Marad tehát két nem triviális eset. Ha 2-essel kezdünk, akkor maradnak a 0, 2, 5 számjegyek, ha pedig 5-össel kezdünk, akkor marad egy 0 számjegy és két darab 2-es számjegy.
Válasszuk szét az eseteket aszerint, hogy mi a legalsó szám, vagyis ha van egy tornyozott hatvány, akkor milyen szám szerepel a legalsó szinten. Ez a szám lehet 1, 2, 3 vagy 4 jegyű. Ha egyjegyű, akkor az 2-es vagy 5-ös, ezt már megbeszéltük. Ha kétjegyű, akkor lehet 20, 22, , 25, 50, vagy 52. Ha háromjegyű, akkor lehet 202, 205, 220, 225, 252, 502, 520, 522. Vegyük észre, hogy ezek a háromjegyű számok a kétjegyű számok lehetséges folytatásai a maradék számjegyek valamelyikével, és követtük a kétjegyű számok sorrendjét, nehogy valamit kihagyjunk. Ami pedig a lehetséges négyjegyű számokat illeti, azokból ugyanannyi van, mint a háromjegyűekből, hiszen csak a negyedik kimaradó számjeggyel tudjuk folytatni a háromjegyű számokat.
Ha az alap négyjegyű, akkor több számjegy nem marad már, tehát a szám maga az eredmény. Ha az alap háromjegyű, akkor a kimaradó számjegynek a kitevőbe kell kerülnie, így itt sincs már választási lehetőség, viszont ne felejtsük el, hogy ha a kitevő 0, akkor az eredmény az alaptól függetlenül 1 lesz. Tehát például a 225, 252 és 522 ugyanazt a számot fogják eredményezni, hiszen 2250 = 2520 = 5220 = 1.
Ha az alap kétjegyű, akkor a torony lehet két- vagy háromszintes, de az esetek száma függ attól, hogy a maradék számjegyek különböznek-e, és a 0 köztük van-e. A lehetséges esetek rendre az alábbiak, ahol a ^ jel a hatványozást jelöli, és az 1 értékű kifejezéseket nem írtuk le:
Ha az alap 20: 20^25, 20^52, 20^2^5, 20^5^2.
Ha az alap 22: 22^50, 22^5^0 = 22.
Ha az alap 25: 25^20, 25^2^0 = 25.
Ha az alap 50: 50^22, 50^2^2.
Ha az alap 52: 52^20, 52^2^0 = 52.Ugyanakkor még ezek között is van két azonos érték, ugyanis 20^25 = 20^5^2.
Ezek után nézzük azt az esetet, amikor egyjegyű szám van az első szinten. Ennek egy alesete, amikor négy emelet magas a hatványozási torony, vagyis minden szinten egyjegyű számok vannak. Ekkor érdemes megnézni, hogy hol van a nulla. Ha a második szinten, akkor a torony értéke 1 lesz, ilyen már volt. Ha a nulla a harmadik szinten van, akkor a torony értéke 2 vagy 5 lesz, ha pedig a torony tetejére kerül a nulla, akkor 2^2, 2^5 vagy 5^2 lehet a végeredmény, de 25 már volt korábban is.
Végül marad az az eset, amikor a toronynak három szintje van, és a második vagy harmadik szinten kétjegyű szám van. Ebben az esetben ha a nulla nem a kétjegyű szám utolsó számjegye, akkor nem kapunk a korábbiakhoz képest új variációt a végeredmény tekintetében, tehát az alábbi eseteket kell még számba venni: 2^2^50, 2^5^20, 5^2^20, 2^20^5, 2^50^2, 5^20^2.
Összefoglalva: 36 különböző érték lehetséges, ezek pedig növekvő sorrendben a következők: 0, 1, 2, 4, 5, 22, 25, 32, 52, 2025, 2052, 2205, 2250, 2520, 5022, 5202, 5220, 205^2, 502^2, 520^2, 50^4, 202^5, 220^5, 25^20, 20^25, 52^20, 50^22, 20^32, 22^50, 20^52, 5^400, 2^2500, 5^2^20, 2^20^5, 2^5^20, 2^2^50.
Ha szereted a fejtörőket, tekintsd meg korábbi feladványainkat is! Ha megjegyzésed lenne, vagy feladványt javasolnál, írj az eszventura@qubit.hu e-mail címre! Ha pedig tetszik a rovat, akkor ezt a Vendégkönyvben kifejezésre juttathatod.
Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus, kognitív kutató, társasjáték-fejlesztő és bűvész.
