Az előző feladványban egy átrendezési paradoxont kellett feloldani. Arra kerestük a magyarázatot, hogyan lehetséges, hogy a parketták puszta átrendezésével a lefedett terület megváltozni látszik. Nyilvánvaló, hogy a síkidomok által összesen lefedett terület nem változhat meg attól, hogy különböző módon rakjuk őket egymás mellé. Ezért tehát két feloldás lehetséges. Vagy nem azonosak a síkidomok a két oldalon, csak ez figyelmen kívül marad, vagy az marad figyelmen kívül, hogy a síkidomok nem illeszkednek hézagmentesen, és valójában nem változott meg a terület. Tehát egyfajta optikai csalódásról, illetve csalásról van szó.

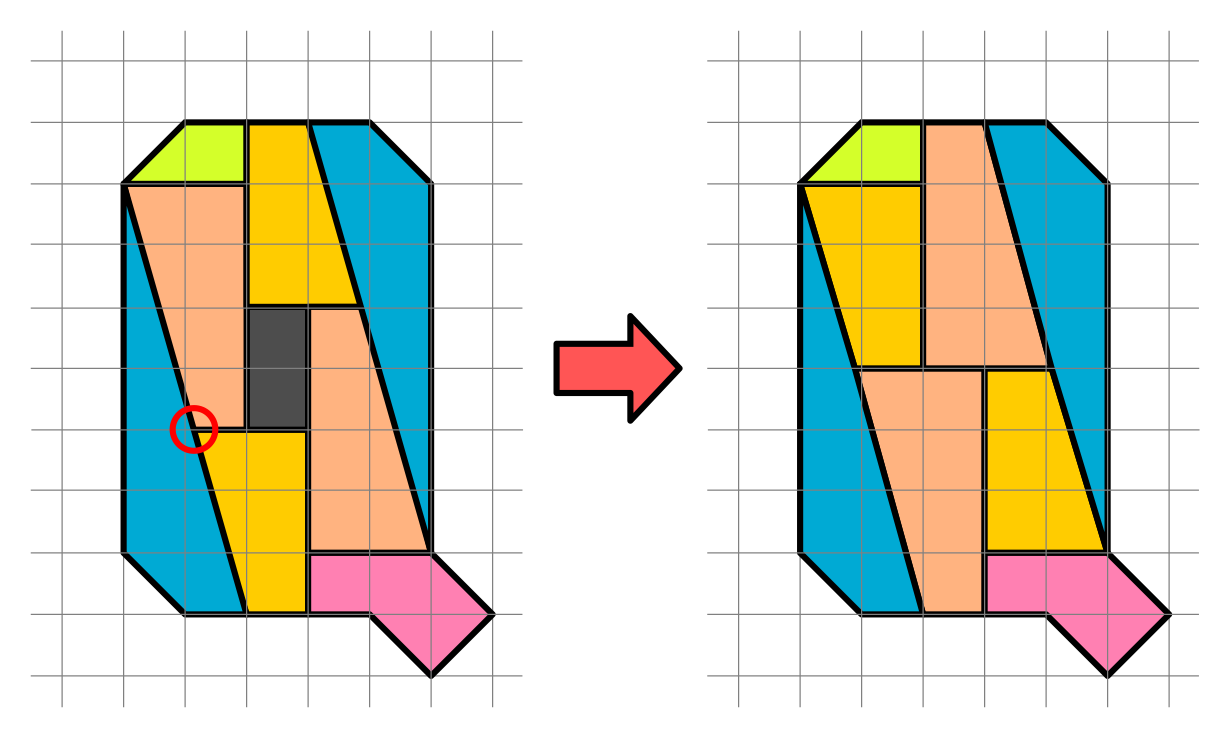
A fenti ábrán segítségképpen behúztuk a rácsvonalakat. A trükk abban rejlik, hogy az eredeti ábra azt sugallta, hogy minden parketta egy rácssokszög, azaz minden parketta minden csúcsa rácspontra esik. A pirossal bekarikázott csúcspont azonban nem lehet rácspont, ha a kékes idom hosszabbik ferde oldala egy olyan egyenes, ami 2 vízszintes egység távolságon 7 függőleges egységet emelkedik. Bár közel van egy rácsponthoz, éppen 1/7 egységnyivel esik tőle jobbra. Így tehát például a barack színű trapéz rövidebbik vízszintes oldala nem 1 egység, ahogy azt a jobb oldali ábrán félrevezetően rajzoltuk, hanem csak 6/7.

Ezt az illúziót vagy paradoxont természetesen kétféle módon is lehet tálalni. A jobb oldali ábrán használhatjuk pontosan a bal oldali ábrán szereplő parkettákat, és a keletkező hézagokat elfedhetjük a vonalvastagsággal, a gyakorlatban meg az alig észrevehetően vastagabb fugákkal. Vagy az elemeket picit korrigálva és egymáshoz igazítva szüntethetjük meg a réseket, ezt a grafikai csalást alkalmaztuk jelen esetben, és azon túl, hogy a barack és sárga trapézok területét picit megnöveltük, ha jobban megfigyeljük a jobb oldali elrendezést, akkor az is látható, hogy a kékes elem hosszabbik ferde oldala valójában egy picikét kidudorodó törött vonal. Optikailag azt használtuk ki, hogy az 1:3, 1:4 és 2:7 egymástól különböző, de nagyon hasonló meredekségeket szabad szemmel nem könnyű egymástól megkülönböztetni.