Maxwell négy egyenlete, amely elindította a technikai forradalmat
Az előző részben ismertettük a klasszikus fizika csúcspontját jelentő elektromágneses elmélet történetét és jelentőségét, most úgy mutatjuk meg Maxwell egyenleteit, hogy annak fizikai tartalma érthető legyen a differenciálegyenletek felírása nélkül is.
A folytonosság paradigmája a klasszikus fizikában
Luigi Galvani békacomb-kísérleteitől indulva történelmi távlatban rendkívül rövid idő alatt teljesedett ki az elektromágnesesség klasszikus elmélete (az olasz fiziológus nevezetes publikációját 1791-ben jelentette meg). Mielőtt továbblépnénk, érdemes elgondolkozni rajta, hogy mi jellemezte ennek a korszaknak a gondolkozását, és minek köszönhető a tudomány látványos fejlődése. Ha egyetlen fogalmat akarunk kiemelni, akkor a folytonosságot kell megemlíteni. Úgy képzelték el, hogy a tér folytonos, az idő folytonos, folytonos a mozgás is, az anyag és jellemzői a tömeg és a töltés is folytonosan tovább osztható.
Ebből indult ki Newton is, amikor a fizikában bevezette a differenciálok fogalmát, amely a folytonosság elvének matematikai továbbfejlesztése a függvények birodalmában. Felismerte, hogy a makrovilág bonyolult törvényei sokkal egyszerűbbek, ha elmegyünk a végtelenül kis változások tartományába, és differenciálegyenletekkel fogalmazzuk meg a legfontosabb összefüggéseket. Ez az út látványos eredményeket hozott a mechanika elméletében, és ez segítette elő a termodinamika és az elektromágnesesség törvényeinek megalkotását - Maxwell is így írta fel egyenleteit.
A végtelenül kis változásokból viszont el kell jutni a makroszkopikus törvényekig. Ebben adta meg az útmutatást a zseniális német matematikus, Carl Friedrich Gauss (1777-1855). Az integrálszámításban a végtelenül apró elemekből végtelenül sokat összeadva juthatunk el a makroszkopikus törvényekig. A differenciálszámításban a skaláris és vektoriális műveleteket (gradiens, divergencia, rotáció) meg kell fordítani, és ennek törvényeit adta meg Gauss. Emiatt a Maxwell-egyenleteknek is két formáját szokás megadni, az egyik a differenciális, a másik az integrális alak.
Töltés és áramsűrűség
A szuperpozíció elve szerint különböző töltések és áramok hatása összeadható. Bár az atomfizika a töltést már elemi egységekre bontja az elektrontöltés többszöröseként, a gyakorlatban mégis használhatjuk a folytonosság elvét a töltések óriási száma miatt, amelynek nagyságrendjét az Amado Avogadró olasz fizikusról elnevezett Avogadro-szám (600 000 000 000 000 000 000 000) adja meg. Ennek megfelelően kiválaszthatunk egy kis dV térfogatot, amelyben még mindig nagyon sok töltés van. Ha ez a tartomány elég kicsi, akkor ezen belül a töltések sűrűsége, valamint a töltések sebessége, azaz az áram, állandónak vehető, amiért bevezethetjük a töltéssűrűséget ρ = dq/dV és az áramsűrűséget: j = dJ/dV. (Itt dq és dJ a dV elemi térfogat töltése, illetve a benne folyó áram). A Maxwell-egyenletekben a sűrűségekből kiindulva határozhatjuk meg az elektromos és mágneses mezőket. Az első törvény mondja ki, hogy az elektromos mező forrása a töltéssűrűség, a második szerint a változó mágneses mező maga körül cirkuláló (körbeforgó) elektromos mezőt kelt, a harmadik törvény kimondja, hogy nincs mágneses töltés, a negyedik törvény szerint a cirkuláló mágneses mezőnek két forrása van: egyrészt az áramsűrűség, másrészt az elektromos mező változása.
A Maxwell-egyenletek fizikai tartalma
A köznapi gondolkozás számára komoly kihívást jelent, hogy megbarátkozzon a vektorok differenciálegyenleteivel, ezért ezek bemutatása helyett megelégszünk az egyenletek tartalmi ismertetésével, abban a reményben, hogy az olvasó számára az elektromágnesesség törvényei így is világosak lesznek. Az első Maxwell-törvény, voltaképpen a Gauss-törvény, amit nevezhetünk forrástörvénynek is, ekvivalens a nyugvó töltés Coulomb-formulájával. Ezek szerint az elektromos mező nagysága, ha a töltés köré különböző sugarú gömböket rajzolunk, fordítottan arányos a gömbök felületével, más szóval a mezőerősség a távolság négyzetével csökken. Ezt szokás szemléltetni erővonalakkal, amelyek bármely távolságban ugyanakkora számban metszik a gömb felületét. Ennek értelmében nevezhetjük a Gauss- törvényt az erővonalak megmaradási törvényének. A harmadik Maxwell-egyenlet ennek ikertestvére lehetne a mágneses mező felépítésében, viszont az elektromos töltésnek nincs mágneses megfelelője, azaz nincs mágneses monopólus. A szimmetriát kedvelő fizikusok ebbe nem nyugodtak bele, ezért létrejött egy „fizikus szekta”, akik kiegészítették ezt az egyenletet valamilyen kísérletileg sohasem látott mágneses monopólussal.
Persze ha létezne mágneses töltés, akkor mágneses áram is lenne, ezért a második Maxwell-egyenletet is bővíteni kellene. Evvel teljes szimmetriát kapnánk az elektromos és mágneses mezők között, de hát a természet – bár szereti a szimmetriát – sohasem törekszik a tökéletes szimmetriára. Sőt épp a szimmetriától való eltérés a fizikai jelenségek talán legfontosabb mozgatórugója. Újabban ebből indult ki a Nobel-díjas elméleti fizikus, Peter Higgs is, amikor szimmetriatöréssel értelmezte a részecskék eredetét. Ha létezne mágneses monopólus, akkor az elemi részecskéket is fel kellene ruházni evvel a tulajdonsággal, és az sem lenne igaz, hogy a mágneses mező értelmezhető lenne az elektromos kölcsönhatás relativisztikus hatásaként. Ezért a magunk részéről nem akarunk a mágneses monopólusok kérdésével a továbbiakban foglalkozni.
De honnan származik a mágneses mező, ha nincs közvetlen forrása? Erre adta meg a választ a francia fizikus, André-Marie Ampère (1775-1836), amikor megállapította, hogy az elektromos áram – azaz a mozgó töltés – maga körül forgó mágneses mezőt hoz létre. Ezt egészítette ki Maxwell a negyedik törvényben, de mielőtt erre rátérnénk, beszéljünk a második törvényről, amelyet az angol Michael Faraday (1791-1867) állapított meg. Ez kimondja, hogy az elektromos mező nemcsak a töltés sztatikus hatásától származik, amit az első törvény mond ki, hanem akkor is létrejöhet, ha a mágneses mező változik. Ez a másodlagos elektromos mező a mágneses mező erővonalait öleli körül.
Maxwell negyedik törvénye az Ampère-törvény kiegészítése egy új taggal, amit eltolódási áramnak is hívnak, mert az elektromos mező változása olyan hatást kelt, mint a mozgó töltések. Az új tag azt írja le, hogy az elektromos mező időbeli változása mágneses mezőt indukál az erővonalak körül ott is, ahol nem folyik áram. Miért lett ez a kiegészítés, amiről az amerikai Richard Feynman is olyan szépen írt, óriási jelentőségű? Ennek oka, hogy szimmetrikus hatást hoz létre a két mező között, az egyik időbeli változása létrehozza a másikat, amelyik körülötte forog, és ez a hatás mindkét irányban megtörténik. Evvel a mechanizmussal gerjeszti egymást a két mező. Emiatt az elektromágneses mező leválik forrásáról, a töltésről és áramokról, és önmagában létező fizikai szubsztancia lesz. Ott lesz tehát a vákuumban a két egymást körülölelő mező. amely fénysebességgel terjed a térben. Ennek matematikai oka, hogy a két mezőt összekapcsoló egyenlet – amit hullámegyenletnek nevezünk – olyan megoldással rendelkezik, amely előírja a fénysebességű haladást. Ez a hullám pedig nem más, mint maga a fény! De nemcsak a fény, hanem a rádióhullám, a gamma- és röntgensugarak is így jöhetnek létre. Voltaképp egész távközlési technikánk alapja a Maxwell által felismert eltolódási áram.
A Lorentz-erő
A Maxwell-egyenletek kizárólag az elektromágneses mező idő- és térbeli változásával, illetve keletkezésével foglalkoznak, de nem mondják meg, hogy maga az elektromágneses mező milyen erőhatást gyakorol. Ezt adja meg a Lorentz-erő, amely szerint az elektromos mező a mozdulatlan, míg a mágneses mező a mozgó töltésre hat:
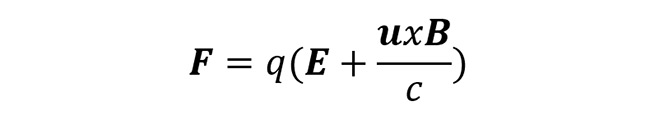
Ez az erő szolgáltatja az elektromos és mágneses mezők definícióját is: az elektromos mező az egységnyi töltésre gyakorolt erő, míg a mágneses mező az u sebességgel mozgó egységtöltésre ható erőt írja le. A Lorentz-erőben megjelenő u/c együttható mutatja, hogy a mágneses mező voltaképp az elektromos kölcsönhatás relativisztikus effektusa. Viszont fény esetén a mágneses és elektromos mező egyenrangú társakká válnak, mert itt az u/c faktor az u = c sebesség miatt egységnyi lesz.
A Maxwell-egyenletektől a modern fizikáig
A Maxwell-egyenletekből két út vezet a modern fizikához. Egyrészt az egyenletek szimmetriája megfelel a relativisztikus szabályoknak, így hozzájárulnak a relativitáselmélet megszületéséhez is. Másrészt, bár az elmélet folytonos töltésekre és áramokra épül, mégis olyan az elektromágnesesség hullámegyenlete, amely összhangban van a kvantummechanika állapotegyenletével, a Schrödinger-egyenlettel. Ezek az egyenletek nemcsak betetőzték a klasszikus fizika fejezetét, hanem alapot adtak a modern fizika huszadik századi forradalmának is.
A szerző fizikus, a BME és az ELTE címzetes egyetemi tanára. Sorozatának korábbi darabjai:
