Mi történik, amikor belépünk egy sötét szobába, és felgyújtjuk a villanyt?

Belépünk a sötét szobába, és felgyújtjuk a villanyt. Először csak körülnézünk, látjuk a különböző tárgyakat, majd megáll a szemünk egy piros virágon az asztal közepén elhelyezett vázában. Milyen egyszerű, mennyire hétköznapi mindez, és mégis mennyire bonyolultak a mögötte lévő fizikai, kémiai, biológiai és pszichikai folyamatok!
Mi történik ilyenkor? Amikor felkapcsoljuk a villanyt, útnak indítjuk az elektronokat két különböző feszültségű vezeték között. Az elektronok a fématomok között kiépített sztrádán száguldanak, amíg a lámpa égőjéig jutnak, ahol már göröngyös földút vár rájuk, állandó ütközéssel, rázkódással. Az elektronok emiatt sok energiát vesztenek, ami az égőszál atomjait felhevíti és izzásba hozza. A gyors rezgésbe hozott elektronok sugározni kezdenek, és ez a sugárzás eljut a szoba minden pontjába. A fény nekiütközik a tárgyaknak, ott részben elnyelődik, részben visszaverődik, de ennek mértéke más és más az egyes tárgyakon és ez függ a fény hullámhosszától is.
A visszavert sugarak egy kis része épp a szemünkbe érkezik, ahol bonyolult folyamatok egész sorát indítja meg. A szemlencséhez érve kölcsönhatásba kerül az ottani molekulák elektronjaival, amelyek megváltoztatják a sugarak irányát. A sugarak az első pillantáskor szétszóródnak, és eljutnak a retina pálcikáihoz, majd amikor a piros virágra koncentrálunk, akkor a lencse által fókuszált fénysugarak a sárga folt sűrűn pakolt csapjaihoz érkeznek meg. Az ott lévő pálcikák és csapok más-más hullámhosszú fénysugarakat nyelnek el, majd szabadítanak ki elektronokat, melyek az idegpályákon szaladnak tovább, hogy az agyba eljutva máig nehezen érthető reakciókat indítsanak el, összegezve a két szemből és a különböző színekre érzékeny pálcikákból, csapokból érkező információt, hogy kialakuljon bennünk egy összesített kép az egész szobáról, a tárgyak elhelyezkedéséről és a virág színéről. Ha csak nagy vonalakban akarjuk érteni, hogy egyetlen pillanat alatt mi minden történik bennünk a legkülönbözőbb tudományágak ismeretére lenne szükségünk. Mi a továbbiakban megmaradunk a fizika mellett.
Sugár sugár hátán: a centiméteres mikrohullámtól a kemény röntgenig
Az ezerarcú elektromágneses sugárzás egyaránt nélkülözhetetlen társunk mindennapi életünkben, és legfontosabb információforrásunk az anyag szerkezetének megismerésében. A legkisebb energiájú, hosszúhullámú rádióhullám a hírközlés alapvető közvetítője az adó és a vevő berendezések között, és ezen alapul az atommagok mágneses tulajdonságait felhasználó rezonanciaspektroszkópia, az NMR, ami talán a legsokrétűbb információt nyújtja a szerves molekulák szerkezetéről, beleértve a fehérjéket is. A módszer nélkül a gyógyszeripar már nem tudna meglenni, de hasznos szerepet játszik az orvosi diagnosztikában is, ahol a belső szervek tomográfiai feltérképezésére használják.
A következő tartományt a mikrohullámú sütők által használt, centiméteres mikrohullámok jelentik, amelyeket a szerkezetkutatásban az elektron mágneses tulajdonságára építő módszer, az elektronspinrezonancia-spektroszkópia hasznosít. A millimétertől a mikronokig terjedő birodalomba vezet át az infravörös (IR) hullám. Neki köszönhetjük, hogy a nap melegét élvezni tudjuk, a spektroszkópiai szerkezetkutatásban pedig ez a sugárzás nyújt betekintést arról, hogyan vibrálnak, forognak az egyes atomok és atomcsoportok a molekulában. A fény, a látható, csodálatos fény jön ezután, ennek jelentősége nyilvánvaló. Túl a látható tartományon következik az UV (ultraviola) tartomány - ennek köszönhetjük bőrünk barna színét és a D-vitamint. De jó, ha vigyázunk vele, mert bőrünkön sebet ejthet - szerencsére ezt a veszélyt mérsékli a sztratoszféra ózon rétege. A szerkezetkutatásban pedig a molekulák elektronjainak különös világába pillanthatunk be az UV-sugarak segítségével.
Ezután már sokkal keményebb sugarak jönnek, amelyek áthatolnak testünkön is. Itt van a rejtélyes X- vagy röntgensugár, amivel testünket átvilágítva kirajzolódik csontszerkezetünk. Az anyagvizsgálatban pedig a kristályokon elhajló sugarak diffrakciója által fényképet készíthetünk a molekulák geometriájáról. Az atommagok belsejéből érkező gammasugarak is segítenek az orvoslásban, például a rák elleni küzdelemben, az atomfizikusok pedig általuk látnak bele az atommagok belsejébe.
Az elektromágneses hullámok alapvető jellemzője a frekvencia, mert fénysebességű terjedésük miatt ez egyben elárulja hullámhosszukat és energiájukat is. Lássuk hát legfontosabb képviselőit a táblázatban.

Száz évvel Newton után kezdődött
Az elektromágnesesség tudományos térhódítása száz évvel Newton után indult el, amikor egy kíváncsi olasz orvos és teológus, Luigi Galvani békacombokkal kezdett el kísérletezni, és felfedezte, hogy az állat combján átszúrt rézkampóhoz vasat érintve a békacomb összerándul - különösen akkor, ha az egyik fém a gerincvelőt, a másik az izmot érinti. Felismerését 1791-ben tette közzé „Kommentár az elektromos erők és az izommozgás kapcsolatáról” címmel. Galvani kortársa, a szintén olasz fizikus, Alessandro Volta ismerte fel 1792-ben, hogy a jelenség alapja a két fém érintkezése, amely villamos áramot indít meg, ha a fémek bizonyos folyadékba merülnek.
A két olasz tudós után egy francia, Charles Augustin de Coulomb vezette be az elektromos töltés fogalmát és írta fel két töltés kölcsönhatását:
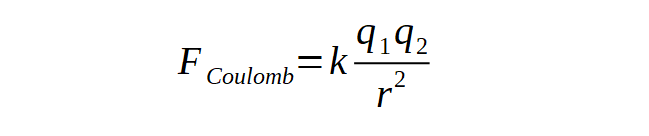
Amikor az atomokban és molekulákban határozzuk meg az elektron energiáját, akkor a k együtthatót szokás egységnek választani: ez annak felel meg, hogy a töltést az erőtörvény segítségével definiáljuk. A gyakorlatban kialakult elektromos egységek esetén az elektromos áram és feszültség alapján adjuk meg a töltést, ahol az áram egysége, az amper annak felel meg, hogy két egymástól 1 méter távolságban lévő párhuzamos vezető között mekkora vonzó, illetve taszító erő lép fel (definíció szerint 2x10-7 N). A töltés egysége, a coulomb pedig az elektromos áram nagyságához kapcsolódik: 1 A áramot kapunk, ha másodpercenként 1 C töltés halad át egy vezetőn. Az 1 C töltés egyébként az elemi töltés 6,2415x1018 szorosa, vagy másképp fogalmazva az elemi töltés értéke qe = 1,6022x10-19 C. Ebben az egységrendszerben k = 1/4𝜋ε0, ahol ε0 = 8,854·10-12 A·s/V·m, amit a szakirodalom a vákuum dielektromos állandójának nevez.
A szerző fizikus, a BME és az ELTE címzetes egyetemi tanára.