Sorozatunk előző részében az elektromágneses sugárzás történetével és legfontosabb tulajdonságaival ismerkedtünk meg, de az elektromágnesesség mellett van egy másik olyan kölcsönhatás, amely döntő szerepet játszik mindennapi életünkben: a gravitáció. A két távolba ható erő sok hasonló tulajdonsággal rendelkezik. Mindkét erő az r távolság négyzetével csökken, és arányos a kölcsönhatásban lévő objektumok alapvető fizikai jellemzőjével, ami a gravitációnál az objektumok m tömege, az elektromos kölcsönhatásnál pedig a q elektromos töltés.

A gravitáció elméletének története

A gravitációs erő formulája Isaac Newtontól származik, akit ma joggal nevezhetünk matematikusnak, csillagásznak és fizikusnak is, bár magát természetfilozófusnak tartotta. Nevezetes műve először 1687-ben jelent meg Philosophiæ Naturalis Principia Mathematica (A természetfilozófia matematikai alapelvei) címen. De ejtsünk egy szót a mecénásról, Edmund Halley-ről is, akinek nagyvonalú támogatása nélkül nem jelenhetett volna meg a mű. Ebben fogalmazta meg Newton a mechanika alaptörvényeit és adta meg a tömegvonzás egyenletét:

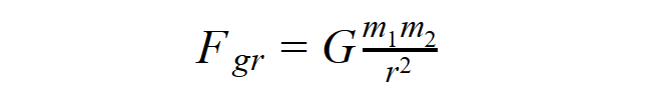
ahol G = 6,674,10^-11m³/kg·s² az általános gravitációs állandó.

Sok nagy felfedezés úgy születik meg, hogy a tudós összekapcsol és egyesít látszólag különböző jelenségeket és törvényeket. Newton felismerte, hogy az az erő, amely a testek tömegét a földhöz vonzza, és ami szabadesésre készteti az elejtett tárgyakat, azonos avval, ami a bolygókat a Nap körül pályán tartja. Ez a jelentős felismerés tette lehetővé, hogy magyarázatot nyerjünk a Johannes Kepler által a bolygómozgásra felírt három törvényre is.

Newton szintén jelentős eredményeket ért el az optika területén, neki lehet tulajdonítani a fény korpuszkuláris elméletét, bár részletesen vizsgálta a fény interferencia-jelenségét is. Bár kora nagy géniuszának számított, követésre méltó volt szerénysége, amit híres mondása jellemez „If I have seen further it is by standing on the shoulders of giants” (Ha messzebbre láttam, azért volt, mert óriások vállán álltam).

A gravitáció és elektromágnesesség

Az előző részben mutattuk be, hogy két töltés, q₁ és q₂, mekkora erővel hat egymásra a Coulomb-törvény szerint:

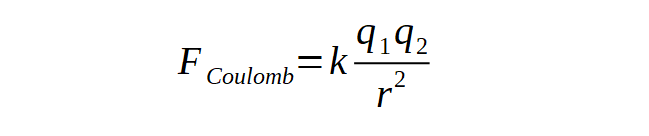
Gondoljuk végig, hogy a két matematikailag azonos szerkezetű törvényben mi az erő és az erő forrásának tekintett fizikai mennyiség, azaz egyfelől a tömeg és másfelől az elektromos töltés viszonya. Ahhoz, hogy egy fizikai törvényhez eljussunk, azt kell biztosítani, hogy a törvényben szereplő minden egyes mennyiségnek legyen egymástól független definíciója, azaz mérési utasítása. A G általános gravitációs állandó méréséhez szükség van két tömegnek (m₁ és m₂) és a közöttük ható gravitációs erőnek a mérésére. A tehetetlen tömegeket mérhetjük a gravitációs törvény alkalmazása nélkül is, ha például egy a rúgóra akasztott tömeg rezgési frekvenciáját határozzuk meg. A gravitációs vonzást is mérhetjük, ha a két tömeget egy vízszintes síkban elforduló tengelyre helyezzük, és a két tömeg közé rugót teszünk. A vonzás miatt a rugó összenyomódik, és a hossz változásából meghatározhatjuk a tömegek között ható vonzóerőt.

Ennél jóval pontosabb mérést végezhetünk el torziós ingával, például Eötvös Loránd is így határozta meg a tehetetlen és a gravitáló tömeg azonosságát, de itt most a hangsúly a mérési lehetőségen van.

Evvel összehasonlítva a Coulomb-törvényt, ami torziós ingával végzett mérésekből származott, ez esetben nincs arra lehetőség, hogy meghatározzuk az erőtörvényben szereplő töltéseket olyan mérésekkel, amelyek nem támaszkodnak ilyen vagy olyan módon az elektromágneses kölcsönhatásra. Emiatt a töltésnek – eltérően a tömegtől – nincs a kölcsönhatástól függetlenül megadható egysége.

További kérdés, hogy a tömeghez hasonlóan van-e „tehetetlensége” az elektromos töltésnek is gyorsításkor? A válasz igen! Amikor az elektronokat gyorsítjuk, sugárzás lép fel, ami energiaveszteséget okoz. Ennek következtében a gyorsító erőnek nem csak a tömeggel arányos kinetikai energiát kell növelni, hanem további erő szükséges a töltéssel arányos fékezési veszteség pótlására is Ez a többleterő arányos a gyorsulás és a töltés szorzatával, hasonlóan a Newton-törvényhez, amelyben az erőt a gyorsulás és a tömeg szorzata adja meg. Két fontos különbség azonban fennmarad a két törvény között: egyfelől a fékezési sugárzás mértéke függ az elektromágneses kölcsönhatás erősségétől is, tehát nem kapunk az elektromágneses kölcsönhatástól független információt a töltés nagyságára; másrészt, amíg a tömeg gyorsítását nem kíséri semmilyen sugárzás, addig a töltés gyorsítása sugárzás kibocsátásával és ezáltal energiaveszteséggel jár.

A kölcsönhatási erő forrása és tárgya

A két erőtörvény abban is hasonló, hogy szimmetrikus szerepet tölt be az erőhatás forrása (például m₁ és q₁) és az erőhatás tárgya (például m₂ és q₂), azaz a vonzhatóság vagy taszíthatóság. Annak külön jelentősége van, hogy nincs „kevert” kölcsönhatás, amikor például az m1 tömeg vonzása a q2 töltésre hatna. A kétféle kölcsönhatás tehát teljesen elkülönül.

Az erők pontszerű forrása

A két kölcsönhatás távolságfüggése arra utal, hogy mindkettő a fizikai objektum egyetlen matematikai pontjából indul ki, és a hatás gömbszerűen terjed, magyarázva, hogy miért változik a kölcsönhatás erőssége fordítottan a gömbfelülettel, amely a sugár négyzetével arányos. Ezt fogalmazhatjuk meg az erővonalak törvényével, amely szerint az erővonalak száma nem változik a távolsággal, más szóval az erővonal-sűrűség fordítva arányos a felülettel. Ez a szabály nem minden erőre igaz, például a nukleáris erős és gyenge kölcsönhatásban az erővonalak eltűnnek az atommag sugarán kívül.

A két törvény további közös vonása, hogy nincs megszabva a távolságra alsó határ, tehát elvben nulla távolságban is érvényes, ahol az erő már végtelenül nagy lenne. Itt felmerül a kérdés: létezik-e legkisebb távolság, amelynél nem kerülhet közelebb egymáshoz két fizikai objektum; van-e valamilyen saját sugár, ami megakadályozza a további közeledést? Ha van, akkor ez egy olyan további erőhatás, amely legyőzi az elektromágneses és gravitációs vonzóerőt. Bizonyos értelemben ennek szerepét játssza el a kvantummechanikában a bizonytalansági elv, amely nem teszi lehetővé, hogy az elektron pozíciója és impulzusa egyidejűleg tetszőleges pontos értéket vegyen fel: ha két elemi részecske helye megegyezne, és nem mozdulnának el egymáshoz képest (tehát nulla lenne az impulzuskülönbség), akkor sérülne a törvény. A pontszerűség elve viszont komoly gondot okoz az elméleti fizikában, amikor a kölcsönhatási mezők energiáját határozzuk meg, ugyanis a teljes tértartományra kiterjesztett számítás végtelenül nagy értéket ad.

Vonzás és taszítás a kölcsönhatásokban

Az elemi részecskék világában a gravitáció elhanyagolható, mert erőssége sok-sok nagyságrenddel kisebb az elektromos erőnél. Becsüljük meg ezt az arányt! Két egymástól egy méter távolságban lévő 10,55 μC töltés (az elemi töltés 6,58·10¹³-szorosa) között 1 N erőhatás jön létre. Ez felel meg a gravitáció esetén 122 tonna anyagnak. A tömeg közel felét az egységnyi töltésű protonok teszik ki, melyek tömege 1,66·10^-27 kg. A 122 tonna anyagban 3,67·10³¹ proton van, ennek gravitációs hatása egyenértékű 6,58·10¹³ elemi töltéssel. Mivel az erő a töltések, illetve a tömegek szorzatával arányos, így az anyagban levő pozitív töltések erőhatása, ha ezt nem kompenzálná az ugyanekkora számban lévő negatív töltésű elektron, 3,11·10³⁵-szeresen haladná meg a benne levő tömeg gravitációs vonzását.

Szemléltessük az arányokat Richard Feynman Nobel-díjas amerikai fizikus nyomán egy hasonlattal.

Képzeljünk el egymástól kartávolságnyira egy fiút és egy lányt. A töltések tökéletesen kompenzálják egymást: a protonok és az elektronok száma pontosan megegyezik, így nincs közöttük elektrosztatikus kölcsönhatás. De mi történik, ha a lány egy varázslattal elektronjainak egy százalékát átküldi a fiúhoz? Ekkor a lány pozitív, a fiú nagy negatív töltéssel fog rendelkezni. Mekkora lesz ekkor a vonzóerő közöttük? Talán akkora, amivel fel lehetne emelni a Parlament épületét? Sokkal nagyobb! Talán akkora, amivel a Himalája hegylánc felemelhető? Sokkal nagyobb! Az erő akkora lesz, ami elég lehetne az egész Föld súlyának felemeléséhez is!

Elvi szempontból azonban nem is a nagyságrend a fontos, hanem az, hogy a kölcsönhatási erő az egyik esetben (gravitáció) mindig vonzást hoz létre, míg a másik esetben (elektromosság) egyaránt lehet vonzás és taszítás is, amit a töltés előjelével tudunk jellemezni. Az elektromos kölcsönhatás két eltérő irányának fontos szerepe van az elektromágneses hullámok, azaz a fény létrejöttében is. Amint a LIGO kísérletekből tudjuk, léteznek gravitációs hullámok is, de ezeket az euklideszi tér torzulásának változása idézi elő, fekete lyukak összeolvadása során. Ennek kimutatásához gigantikus méretű, sok kilométer kiterjedésű mérőeszközökre és ezernyi fizikus munkájára volt szükség, míg az elektromágneses hullámok, mint a fény, mindennapjaink állandó résztvevői, köszönhetően a hozzánk eljutó fotonok milliárdjainak. De hogyan járul ehhez hozzá a mágnesesség? Ezt tárgyaljuk a következő részben.

A szerző fizikus, a BME és az ELTE címzetes egyetemi tanára.