Hogyan magyarázza a relativitáselmélet a sanghaji expressz lebegését a sínek felett?
Az előző két részben ismerkedtünk meg az elektromos és a gravitációs erők viszonyával, de honnan származnak a rejtélyesnek tűnő mágneses hatások? Ez sokáig rejtély volt nem csak köznapi gondolkozás, hanem a fizika számára is. A választ a mozgásokban kell keresni, mert amíg nem változik a töltések helyzete, elegendő az elektrosztatikus Coulomb-erőről beszélni, de ha már mozognak, vagyis áramok jönnek létre, fellép egy új erő is: megjelenik a mágnesesség. Eredetileg ezt az erőt függetlennek gondolták az elektromosságtól, és tradicionálisan evvel jellemezték az elektromos áram, valamint a töltés nagyságát is. Ily módon az elektromos töltés definícióját meg lehetett adni látszólag függetlenül a töltések közötti erőhatás mértékétől.
Miért van szükség a kölcsönhatási mező fogalmára?
Makroszkopikus rendszerekben nagyszámú töltött részecske mozog, emiatt gyakorlatilag lehetetlen páronként összegezni a Coulomb-erőket, valamint a mozgó töltések által okozott mágneses hatásokat, szükség van ezért egy új fogalomra, amit mezőnek nevezünk. A hazai gyakorlatban inkább tereket emlegetnek: elektromos és mágneses teret, elmosva a különbséget az angol szakirodalomban használt „space” és „field” szavak között. Helyesebb viszont megkülönböztetni a két fogalmat, és a „field” magyar megfelelőjeként a mező szót használni. További fogalmakat vezet be az elektrodinamika, amikor az elektromos és mágneses hatásokat fizikai közegekben vizsgálja, ilyenek például a dielektrikumok, ahol megváltozik a kölcsönhatások erőssége, ezért szokás megkülönböztetni elektromos és mágneses teret, valamint indukciót. Evvel most nem foglalkozunk, és a mező fogalmára szorítkozunk a továbbiakban. Mező alatt térben változó kölcsönhatást értünk, amely meghatározza az egységnyi töltésre vagy áramra ható erőt.
A mezőfogalom bevezetésének van azonban egy fontos előfeltétele: legyen érvényes a szuperpozíció elve. A szuperpozíció elve egyszerűsíti a bonyolult kölcsönhatások leírását. Nem veszi tekintetbe, hogy két töltés, vagy tömeg között más lehet a kölcsönhatás, ha egy harmadik is „közbeszól”. (Tudjuk, hogy ez az egyszerűsítés mennyire nem igaz, ha az emberek közötti kapcsolatokra gondolunk!) Tehát úgy fogjuk fel három fizikai objektum között a teljes erőhatást, hogy ezt felbontjuk három független kölcsönhatási párra. Matematikailag ez azt jelenti, hogy az elektromos kölcsönhatás kifejezésében csupa olyan tag lesz, amelyben két-két töltés szorzata szerepel és nincs olyan, amelyben három, vagy több töltés szorzata lépne fel. Tapasztalataink szerint a gravitációs és Coulomb-erő megfelel ennek a kritériumnak. Az E(r) elektromos mező azt mondja meg, hogy a tér egy adott pontjában mekkora erő hat az oda képzelt töltésre, míg az egységnyi töltésre ható ϕ(r) elektromos potenciál az energiát adja meg. (Itt és a továbbiakban az irányfüggő, azaz vektoriális mennyiségeket vastag betűvel jelöljük.) Ennek megfelelően az elektromos mező az összes qi töltés Coulomb-erőhatását összegzi:
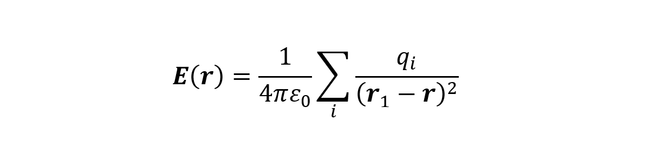
(Az ε0 vákuum dielektromos állandóról a korábbi részben már szó volt). Az E(r) mező és a ϕ(r) skaláris potenciál a kölcsönhatások leírásának két alternatív módja, az egyik az erő nagyságát, a másik a potenciális energiát jellemzi, legyen szó akár gravitációról, akár elektromos hatásról. Szemléltessük a két mennyiség kapcsolatát egy példával: képzeljük azt, hogy felmegyünk egy hegyre. Ekkor a gravitációs erővel szemben végzünk munkát, amelynek nagysága az egyes lépések során a lejtő meredekségével arányos, ha nagy a meredekség, akkor lépésenként nagyobb mértékben nő a potenciális energia. A lejtő meredekségét nevezi a vektor algebra „gradiensnek” és ez adja meg a kapcsolatot az erő ás a potenciál között. Elektromos kölcsönhatások esetén a hegy helyett gondoljunk töltésekre, amiket egy kondenzátorra vittünk fel, és a lejtő meredekségét jellemezzük a kondenzátor két lemeze közötti távolsággal.
De miért mondjuk azt, hogy az elektromos mező képzelt töltésre hat? Ennek oka, hogy az elektromos mező fenti összegzéséből hiányzik az a töltés, amelyre az elektromos mező hatását éppen vizsgáljuk. Ez a definíció viszont problémát okoz, amikor az elektromos és a mágneses mező teljes energiáját számítjuk, hiszen ehhez az adott pontban elhelyezett töltés is hozzájárul. Ez vezet el ahhoz a dilemmához, ami az előző részben a Coulomb-erőhöz tartozó végtelenül nagy energiához vezetett.
Mágneses kölcsönhatás: a mozgó töltés relativisztikus hatása
Eddig a mező fogalmát és annak ellentmondásait elemeztük, és csak utaltunk rá, hogy a mágneses hatást a töltések mozgása váltja ki. De miért csak a mozgás az ok, nem lehet a mágnesességnek is valamilyen saját forrása – hasonlóan az elektromos töltéshez – amit mágneses töltésnek, vagy monopólusnak nevezhetnénk? Ez a kérdés már régóta izgatja a fizikusok fantáziáját, de mindenki által elfogadott választ még nem sikerült találni.
Az eddigiekben nyugvó töltések kölcsönhatását vizsgáltuk, de hogyan változik a kép, ha a két töltés egymáshoz képest valamilyen sebességgel változtatja távolságát? Ebben az esetben már jóval bonyolultabb a kölcsönhatás a töltések között, mert az hogy mekkora erőhatás jön létre a jelenben, attól függ, hogy mi volt a múltban! Ennek megértéséhez meg kell ismerkednünk a retardált idő fogalmával. Ha a tér egy adott A(r) pontjában akarjuk leírni, hogy milyen potenciálfüggvényt hoz létre a B(r’) ponton áthaladó mozgó ponttöltés, akkor figyelembe kell venni, hogy mennyi idővel később fog eljutni a hatás az A pontba, hiszen minden hatás megérkezéséhez idő kell. Sőt, azt is számításba kell venni, hogy a kölcsönhatás nagysága nem a t időben meglévő r távolságtól függ, hanem attól, hogy a korábbi t’ = t – r’/c időben, mekkora volt a két részecske akkori r’ távolsága. A t’ időt nevezzük retardált időnek.
A retardált idő meghatározásánál fontos szerepet játszik a fénysebesség terjedési sebességének állandósága. Itt megjegyezzük, hogy bármilyen erőhatásról legyen szó, annak terjedési sebessége nem haladja meg a fény sebességét vákuumban. Annak megfogalmazása, hogy a hatás sebessége állandó, fontos a tudományos megismerés egyértelműsége miatt is. Ha ugyanis a hatás tényleges bekövetkezési ideje függene a kibocsátó objektum saját sebességétől, akkor nem tudnánk univerzális és reprodukálható törvényeket alkotni az elektromágnesességről, sőt a gravitációról sem. Hogyan tudjuk ugyanis meghatározni két fizikai objektum egymáshoz képesti sebességét? Ez csak úgy lehet, ha létezik valamilyen kölcsönhatás a két objektum és a megfigyelő között, például az egyik helyen kibocsátott fénysugarat a másik helyen észleljük. A megfigyelésnél alapul vesszük, hogy mennyi volt a fény repülési ideje, de ha ez a távolságon kívül a sebességtől is függ, akkor a sebességmérés egyértelműsége csorbát szenved.
A retardáció miatt jön létre a mágnesesség, ennek nagysága az elektromos hatáshoz képest a töltésmozgás és a fény sebességének arányától függ. A relativisztikus hatás és a mágnesesség viszonyát szemléletesen mutatja meg Feynman (R. P. Feynman, R.P. Leighton, M. Sands, „Mai Fizika, VI. 101-105 old., Műszaki Könyvkiadó, Budapest, 1970). Mekkora lesz az u sebességgel mozgó töltésre ható erő, amikor a B pontba érkezik t idő alatt? Ezt a retardációs hatást mutatja az ábra:
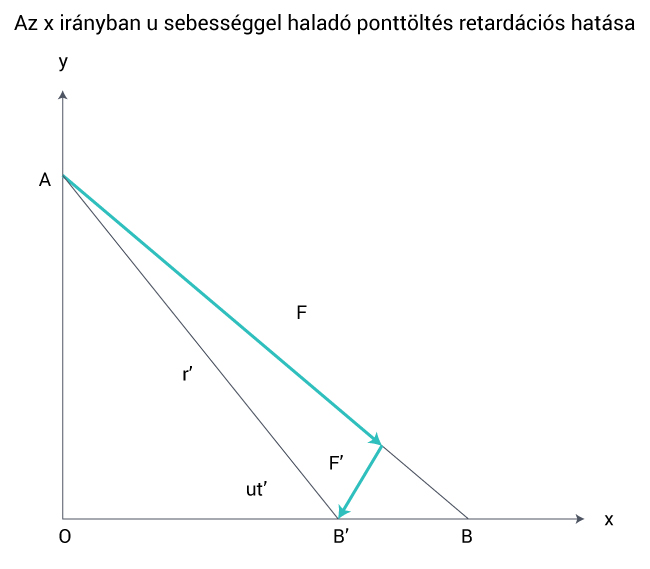
Mivel a fénynek is időre van szüksége, hogy az A pontból megérkezzen B-be, így a B pontban érzékelt erőt egy korábbi t’ idő alapján adhatjuk meg, amikor a töltés még a B’ pontban volt. Az ábráról látható, hogy a Coulomb-erő nem a sztatikus esetnek megfelelő AB irányba mutat, hanem lesz egy erre merőleges F’ komponense is a retardációs hatás miatt. Ez a retardációs erő a B mágneses mezőhöz kapcsolódik, és visszaadja annak nagyságrendjét. A mozgó q töltésre ható tényleges erőt Lorentz formulája adja meg:
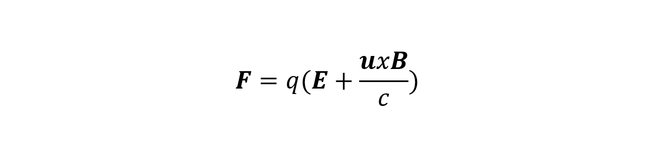
A vektoriális szorzás szabályai szerint ez azt fejezi ki, hogy a mágneses erő merőleges az j = qu áram irányára, ezért amikor a vezetékben áram folyik, azt rá merőlegesen körbeveszi a mágneses mező.
Diamágnesesség és ferromágnesesség
Alkossunk egy kör alakú hurkot, amelyben áram folyik, ekkor az összegződő mező eredője a kör tengelyével párhuzamos lesz, ha sok ilyen hurkot tekercselünk egymás mellé, erős mágneses mező lesz az eredmény, ez az elektromágnes. Viszont a fémes vas elektromos áram nélkül is erős mágneses tulajdonságokat mutat. De milyen áram folyik a vas belsejében, amikor permanens mágnest tartunk a kezünkben? Ez a jelenség már a kvantummechanika rejtélyes világába vezet. Az elektron már önmagában is úgy viselkedik mint egy parányi mágnes, úgy mondjuk, hogy mágneses dipólus. Az anyagok túlnyomó többségében a kémiai kötéseket olyan elektronpárok alkotják, amelyben a két elektron mágnesessége kompenzálja egymást, az ilyen anyagra mondjuk, hogy diamágneses.
De mi történik a vasban, az miért viselkedik olyan különösen? A magyarázatot az atom héjszerkezete adja meg. A külső héj elektronjai hozzák létre a kémiai kötést, de a nagyobb rendszámú átmeneti fémek rendelkeznek egy telítetlen belső héjjal is, amelyben összesen 10 elektron foglalhat helyet. A vas különös tulajdonságát az okozza, hogy ott ez a d-héj félig van betöltve és ennek az öt elektronnak mágnesessége összeadódik. De a ferromágnesességhez kell még valami! Olyan a fémes vas kristályszerkezete, amelyben a szomszédos vas atomok mágnesessége is összeadódik, ami már egy kisebb szemcsének is jelentős mágnesességet ad. Ha az egyes vas szemcsék rendezetlenek, még mindig nincs jelentős mágneses hatás, de a szemcsék külső mágneses mezővel polarizálhatók, és akkor létrejön a permanens mágnes. A mágnesesség dipólus jellegű, ami avval jár, hogy van egy északi és egy déli pólus; ha két különböző mágnesnél ezek iránya megegyezik, akkor erős vonzás jön létre, ha ellenkező, akkor taszítás. Ez a taszító erő olyan nagy, hogy legyőzheti a földi gravitációs erőt is, így tudunk létrehozni lebegő tárgyakat. Ezt járművekben is kamatoztathatjuk, amikor súrlódás nélkül száguldhatnak a vonatok a sínek felett. A sanghaji MAGLEV expressz már 400 km/h sebességgel szállíthat utasokat is.
A csillagok és bolygók mágneses tulajdonságai
Korábban már írtunk róla, hogy a Föld mélyének konvenciós áramlásai is létrehoznak mágnesességet, de ennél sok-sok nagyságrenddel erősebb mező jöhet létre egyes csillagokban. Ilyen erős mágneses mezőnek köszönhető a pulzárokból érkező gammasugárzás is, amely létrejön a gyorsan pörgő neutron csillagokban. Ennek forrása a töltés semleges neutronok saját mágneses dipólus momentuma. De ha nincs töltés, akkor mi hozza létre a mágnesességet? Itt a magyarázat már elvezet a részecskék kvark elméletéhez. Eszerint az „up” kvark pozitív töltését két fele akkora, de negatív töltésű „down” kvark egyenlíti ki, és a töltések eltérő térbeli eloszlása létrehozza a neutron parányi mágnesét, amelyek összegződnek a rendkívül nagy sűrűségű neutron csillagokban.
A következő részben fogunk eljutni a klasszikus fizika egyik csúcspontjához, az elektromágneses kölcsönhatásokat leíró Maxwell-egyenletekhez, amelynek felfedezése új korszakot nyitott a technikai alkalmazásokban és a tudomány történetében.
A szerző fizikus, a BME és az ELTE címzetes egyetemi tanára. Elektromágneses sugárzással foglalkozó sorozatának két korábbi darabja: