A huszárkörút a sakktábla lólépésekkel való bejárása úgy, hogy a huszár minden mezőt pontosan egyszer érint. A probléma legkorábbi ismert említése a kilencedik századba nyúlik vissza. Számos matematikus is foglalkozott a problémával, köztül Leonhard Euler, a matematikatörténet egyik legtermékenyebb alakja. Érdekesség, hogy Kempelen Farkas sakkautomatája, a Török is be tudott mutatni huszárkörutat, nem csak partikat játszott a bemutatókon. Egy 8×8-as táblán egyébként pontosan 13 267 364 410 532 zárt körút létezik. Alább a klasszikus változatnak egy olyan variációja látható, amiben a sakk-készlet mind a négy huszárját használjuk. Vajon ennek is ilyen sok megoldása létezik?

22. feladvány: Huszárok vándorlása

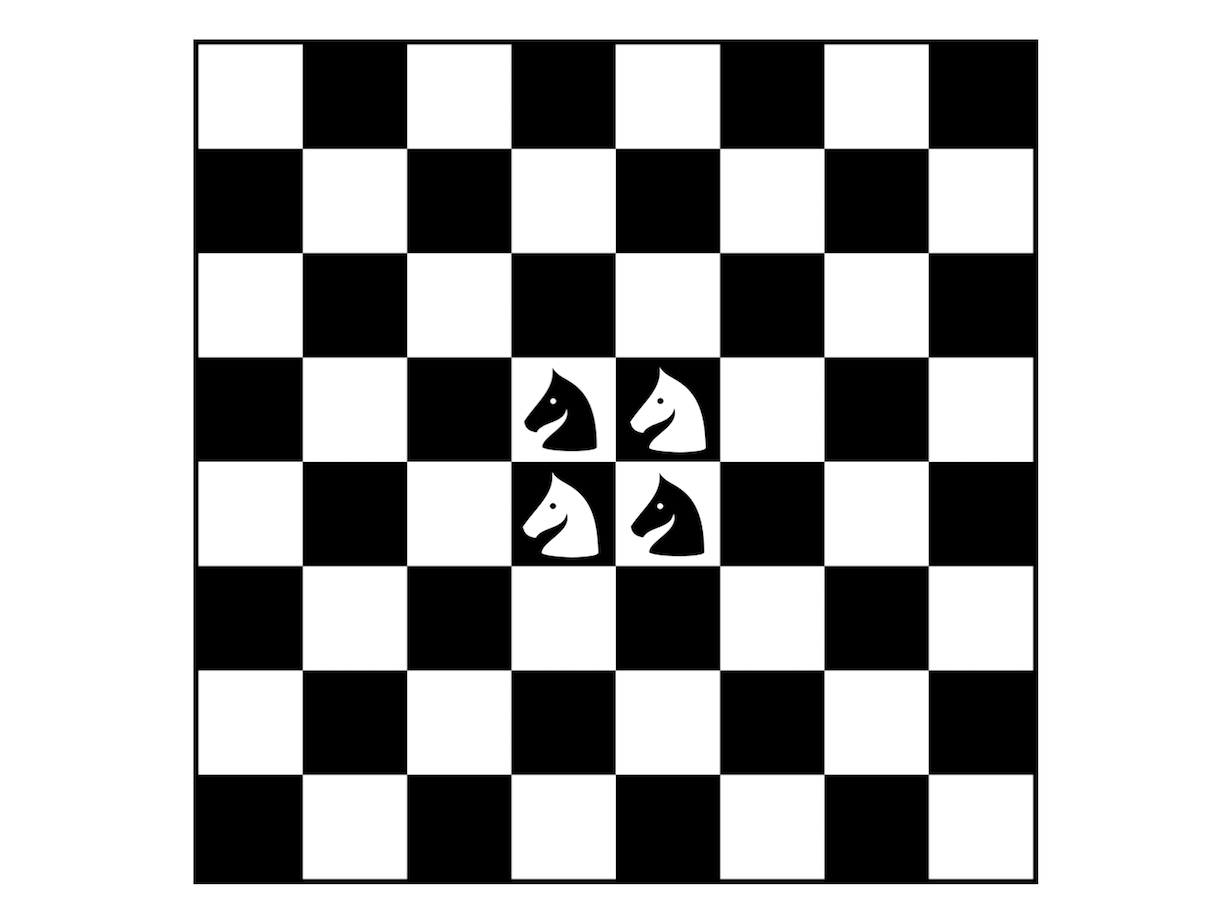
A sakktábla középső négy mezőjén áll a két világos és a két sötét huszár. Szabályos lólépésekkel körbe tudják-e járni úgy a sakktáblát, hogy a sakktábla minden mezőjét pontosan egyszer érinti valamelyik huszár, mind a négyen ugyanannyi lépést tesznek, és a legvégén visszaérkeznek saját kiindulási mezőjükre?

Felajánlott koponyák:

A megfejtéseket az eszventura@qubit.hu címre várjuk. A megoldáshoz kérünk rajzot mellékelni. A legelső megoldók és a legjobb versenyzők felkerülnek az Ész Ventura dicsőségfalára, aki nem kíván ott szerepelni, kérjük, jelezze. Szerepelni álnévvel is lehet, ezért mindenképpen érdemes az év végén kisorsolt nyeremények miatt. Leveleiket kérjük, ékezetesen írják alá. Az e-mail subject mezőjében kérjük feltüntetni, hogy 'megoldás', illetve sorszámmal jelezni, hogy melyik feladványról van szó. Beküldési határidő: június 10. éjfél.

Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus, bűvész