Hogyan osszon el 10 kalóz 100 aranyat?

Tíz kalóz osztozkodik egy száz aranyérméből álló zsákmányon (az érmék oszthatatlanok).

A kalózok vadságuk alapján egyértelmű sorrendbe tehetők, és a legvadabbtól a legszelídebbig sorra tesznek ajánlatot a 100 érme elosztásáról. Egy ajánlat megadja, hogy melyik kalóz hány (egész számú) érmét kap. Először a legvadabb kalóz tesz ajánlatot, majd az összes kalóz szavaz róla, az ajánlattevőt is beleértve. Ha a kalózok 50 százaléka elfogadja az ajánlatot (elég pontosan 50 százalék, nem kell több), akkor az aranyak javasolt kiosztása megtörténik, és az ajánlattevések sorozatának vége.

Ha kevesebb, mint 50 százalék szavazza meg az ajánlatot, akkor az ajánlattevő kalózt ledobják a fedélzetről, és a következő legvadabb kalóz tesz ajánlatot az érmék elosztására a még fedélzeten lévő kalózok között.

A kalózok preferencia-sorrendje a következő: minden kalóz elsősorban a pénzbeli jutalmat preferálja, másodsorban pedig két különböző helyzetben, amikor ugyanazon pénzbeli jutalomban részesül, azt választja, ahol minél több más kalózt dobhat le a fedélzetről. Minden kalóz szeretné elkerülni, hogy ledobják a fedélzetről - ha őt ledobják, akkor vízbe fullad, és ez minden más kimenetelnél rosszabb számára. Minden kalóz racionális, ezt tudják is egymásról, és csak a saját érdeküket veszik figyelembe.

Mi lesz az osztozkodás végeredménye, és hogyan zajlik az ajánlattevés? Mi történik, ha tíz helyett ötszáz kalóz van?

Figyelem: ötszáz kalóz esetén nehezebb és még kevésbé intuitív a megoldás!

Segítség: a végső állásból induljunk ki. Mi történik, ha csak két kalóz van a fedélzeten, és a vadabb tesz ajánlatot? Ha a harmadik kalóz tudja, hogy mi történik két kalóz esetén, akkor milyen stratégiát alkalmaz, hogy elkerülje azt, hogy őt ledobják?

Megoldás

A kalózos feladat egyik változatát egy kaliforniai szoftvermérnök, Stephen Omohundro küldte el évtizedekkel ezelőtt Ian Stewart brit matematikusnak, aki a Scientific American 1999. májusi számában tette közzé a megoldást. Bár az eredeti, tíz kalózos rejtvény akkor már évek óta ismert volt, az ötszáz kalózos változat nem várt módon érdekes, új csavart hozott a megoldásba.

A megoldáshoz a kalózokat megszámozzuk szelídségi sorrendben, azaz a legkevésbé vad kalóz kapja a K1 számot, a második legszelídebb a K2-t, így tovább K10-ig, majd K500-ig. Az ajánlattevés így szám szerint csökkenő sorrendben halad.

Ahogyan azt a segítségben is írtuk, hasonló játékok elemzésénél (melyek végesek, és minden helyzetben minden információ tudott) hátulról érdemes haladni. Mi történik, amikor csak két kalóz marad a fedélzeten? K2 tesz ajánlatot. Akármi is az ajánlat, ő maga megszavazza azt, és így megszerzi a szavazatok 50 százalékát. Tehát K2 100 aranyat juttat magának és 0-át K1-nek, a felosztás pedig elfogadásra kerül K2 szavazatával.

Mit tehet ennek tudatában K3? Tudja, hogy ha őt ledobják, akkor az előbb leírt helyzetre kerül a sor. K2 szavazatát tehát nem tudja megszerezni, neki a lehető legjobb, ha K3-at ledobják, és a következő fázisába kerül a játék, amiben ő 100 aranyat kap. K2 még akkor sem szavazná meg K3 ajánlatát, ha ő 100 aranyat kapna, ugyanis szeretné K3-at ledobni a fedélzetről. Tehát K3-nak a többséghez K1 szavazatát kell megszereznie. K1 nem szavaz meg olyan osztozást, amelyben 0 aranyat kap, hiszen ha semmiképp nem kap aranyat (ugyanis a K2 által javasolt és elfogadott osztozásban sem kap), akkor a másodlagos preferenciája szerint ő is inkább ledobná K3-at. Azonban ha akár csak 1 aranyat is juttat K3 K1-nek, akkor K1 vele szavaz. Így K3 a számára optimális felosztást javasolja: (1, 0, 99) arany (K1, K2, K3)-nek, és ez elfogadásra is kerül K1 és K3 szavazatával.

Hogyan tudja K4 a lehető legkevesebb arany átadásával biztosítani magának a többséget? Mivel, ha K3 kerül sorra, akkor K2 0 aranyat kap, ezért, ha K2-nek akárcsak 1 aranyat is juttat, akkor K2 megszavazza K4 ajánlatát. (Ha K4 magának szánja mind a 100 aranyat, akkor senki sem szavaz vele, inkább ledobják a fedélzetről.) Tehát K4 a következőt javasolja: (0,1,0,99) arany (K1, K2, K3, K4)-nek, ez pedig elfogadásra kerül K2 és K4 szavazatával.

K5-nek legalább 2 szavazatot kell megszereznie a sajátján kívül. Ehhez legalább két megvesztegetési arany kell, hiszen azok, akik 0 aranyat kapnak egy elosztásban, sosem szavazzák meg, hiszen inkább az illető vízbe dobását pártolják. Két megvesztegetési arannyal el is tudja ezt érni: (1,0,1,0,98) aranyat javasol (K1, K2, K3, K4, K5)-nek. K1, K3 és K5 ezt megszavazza, hiszen ha nem tenné, akkor a 4 kalózos helyeztbe kerül a játék, és itt tudjuk, hogy K4 javaslatát fogják elfogadni, amiben K1 és K3 nem kap aranyat.

Láthatjuk, hogy ez a logika működik tovább: mindenki a lehető legkevesebb megvesztegetési arany felhasználásával tesz olyan javaslatot, amelyet elfogadnak. A minta szerint ezt úgy tudják elérni, hogy a páratlan számú kalózok a páratlanoknak, a páros számúak pedig a párosoknak juttatnak 1-1 aranyat, maguknak pedig a maradékot.

Tehát a 10 kalózos változat megoldása: K10 ezt a javaslatot teszi: (0,1,0,1,0,1,0,1,0,96) (K1:K10)-nek, és a javaslatot elfogadják K2, K4, K6, K8 ás K10 szavazatával, a játéknak pedig rögtön vége, senkit sem dobnak a vízbe.

Egyensúlyi helyzetben tehát a legelső javaslattevő, a legvadabb kalóz ajánlatát fogadják el (és ha rá kerül a sor, mindenki olyan javaslatot tesz, hogy az ő ajánlatát elfogadják, hiszen nem akarnak vízbe esni), és egyensúlyi helyzetben emiatt nem is dobnak senkit a vízbe, még a legvadabb társukat sem. A legtöbb aranyat is a legvadabb kalóz kapja, az osztozkodás egy kör után véget ér.

500 kalóz esetén az összes eredmény megváltozik

Az Omohundro által kifejlesztett változatban 500 kalóz osztozkodik. A megoldás pedig olyan lesz, ami a nagyobb igazságérzetűeknek is tetszik: az első pár legvadabb kalózt a vízbe dobják, és a legszelídebb kalózok kapnak a legnagyobb eséllyel aranyat.

Ennek a változásnak a kulcsa Stewart bizonyítása alapján a következő. A fenti, szavazatonként 1-1 aranyat használó lefizetéses módszer 200 kalózig működik háborítatlanul. K200 a páros számú kalózoknak, önmagát beleértve, 1-1 aranyat juttat, és a páros számú kalózok 100 szavazatával el is fogadják ezt az osztozást. K201-nek 101 szavazatot kell szereznie, hogy ne essen vízbe. Önmaga megszavaz bármilyen osztozkodást, hogy túlélje. 100 kalózt le tud fizetni a teljes zsákmány felhasználásával: K1-K199-ig a páratlan számú kalózoknak juttat 1 aranyat, a páros számúaknak és saját magának pedig 0-át. Ezt a javaslatot el is fogadják az összes páratlan számú kalóz szavazatával. 101 kalóz tehát ebben az állásban biztosan nem kap semmit.

K202 még el tudja kerülni a vízbe esést, 101 szavazatra van szüksége. Önmaga megszavazza saját javaslatát, és a 100 megvesztegetési aranyát az előző leosztásban semmit sem kapó 101 kalóz között (K2:K200 párosak és K201) osztja ki. Mind a 100, aki kap aranyat, megszavazza a leosztást, így a saját szavazatával együtt megvan az 50 százalékhoz szükséges 101 szavazata. A páratlan számú K1:K199 kalózok és K202 biztosan nem kap aranyat.

K203-nak közülük kellene megvesztegetnie 101 szavazót magán kívül, ám ehhez nincs elég aranya, így K203 mindenképpen a vízbe kerül, ha ő tesz javaslatot.

Mondhatjuk tehát, hogy az összes K202-nél vadabb kalózt vízbe dobják, mert nincs elég megvesztegetési aranyuk? Nem!

K204 akármilyen javaslatra megkapja K203 szavazatát, ugyanis K203 mindenáron el akarja kerülni, hogy rá jusson az ajánlattevés sora, és vízbe dobják. Tehát a saját és K203 szavazatán kívül K204-nek már csak 100 szavazatra van szüksége. Ezt meg is tudja szerezni, ha a K202 által aranyban biztosan nem részesítettek közül 100-nak juttat 1-1 aranyat, ők 101-en vannak, a K1:K199 páratlan kalózok és K202. Így K204 megmenekül, az ő ajánlatát elfogadják.

K205 magán kívül 102 embert kellene megvesztegessen, amire (K203-hoz hasonlóan) nincs elég aranya. K206 emiatt megkapná K205 szavazatát, ha sikerülne olyan javaslatot tennie, amit a többség elfogad, de saját magán és K205-ön kívül még 101 támogató kell neki, ehhez azonban nincs elé aranya. K207 emiatt számíthat K206 szavazatára, és K205-ére is, hiszen K206 javaslata nem tud átmenni, így K206 és később K205 is vízbe kerül, ha tovább folytatódik az osztozkodás. Ezen, és a saját szavazatán kívül még 101-re van szüksége, ez pedig nem fog neki sikerülni, így, ha K207-re kerül a sor, K207, K206 és K205 is megy a vízbe.

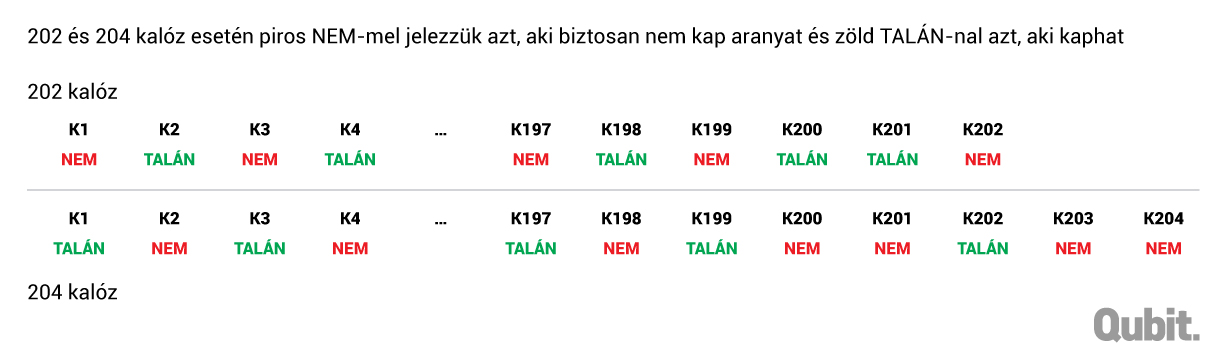
K208 ajánlatát így K207, K206 és K205 is támogatni fogja, és önmaga is megszavazza, így már csak 100 megvesztegetett kalózra van szüksége a szelídebbek közül. Ezt ő már el is érheti, ha a K204 ajánlatában aranyhoz biztos nem jutó K2:K200, K201, K203 és K204 (103 darab kalóz) között osztja ki a 100 aranyat.

Végtelenül folytatódó minta

Egy új minta tűnik tehát fel, ez pedig már végtelenül folytatódik, állapítja meg Stewart. „Azon kalózok sorszámai, akik nyerő osztozást javasolhatnak (mindig 0 aranyat adva maguknak és 1-1 aranyat 100 kalóztársuknak) el vannak választva egymástól olyan kalózok – egyre növekvő – sorozatával, akik a vízbe kerülnek ajánlatuktól függetlenül, és akiknek támogató szavazata emiatt biztosított bármely vadabb kalóz ajánlata esetén.”

Itt pontosíthatunk Stewart eredeti cikkéhez képest: csak azon kalózok ajánlatát szavazzák meg, akiké végül tényleg át is fog menni, a többi esetén agnosztikusak lehetünk a később vízbe kerülők szavazatával kapcsolatban.

Az megoldás így folytatódik: „Azok a kalózok, akik elkerülik a biztos vízbe dobást –K201, K202, K204, K208, K216, K232, K264, K328, K456 és így tovább – azok a kalózok, amelyek sorszáma felírható 200 + kettőhatvány alakban.”

A lefizetésre használt aranyak tulajdonosai pedig K216 esetén K1:K199, K202, K205-208 közül kerülnek ki, és így tovább, K456 esetén pedig a K1:K199 és néhány vadabb kalóz közül kerülnek ki: ezek azok, akik K328 ajánlata alapján biztosan nem kapnának semmit. Egy lehetséges megoldás, hogy mindig a legszelídebb 200 közül választanak, a párosoknak és páratlanoknak váltakozva ajánlják fel a 100 megvesztegetési aranyat, tehát K456 esetén egy lehetséges megoldás, hogy K1:K199-nek juttatja a megvesztegetési aranyakat, az ő szavazataikkal (100 db) és K329-K456 szavazataival (128 darab) megvan neki a szavazatok 50 százaléka, és elkerüli a vízbe dobást.

Tehát 500 kalóz esetén a legvadabbak (pontosan a legvadabb 44) a vízbe kerül, és a legszelídebbeknek van a legnagyobb esélyük az aranyra. Az ajánlattevő pedig, akinek az ajánlatát elfogadják, a legvadabb túlélő, nem kap semmit azon kívül, hogy a fedélzeten maradhat.

A szerző az Oxfordi Egyetem mesterszakos közgazdaságtan-hallgatója. Összes írása a Qubiten itt olvasható.