Ész Ventura: A 2018-as focivébé hivatalos labdája és a térgeometria

Az idei focivébé hivatalos labdájával kapcsolatos térgeometriai feladványnak csupán az volt a titka, hogy neki kellett állni számolni. Ez így egy kicsit unalmasan hangzik, de azért van abban is érdekesség, hogy miként lehet nekikezdeni egy ilyen térgeometriai számításnak, főleg azért, mert legtöbbünknek nem túl jó a térgeometriai érzéke.
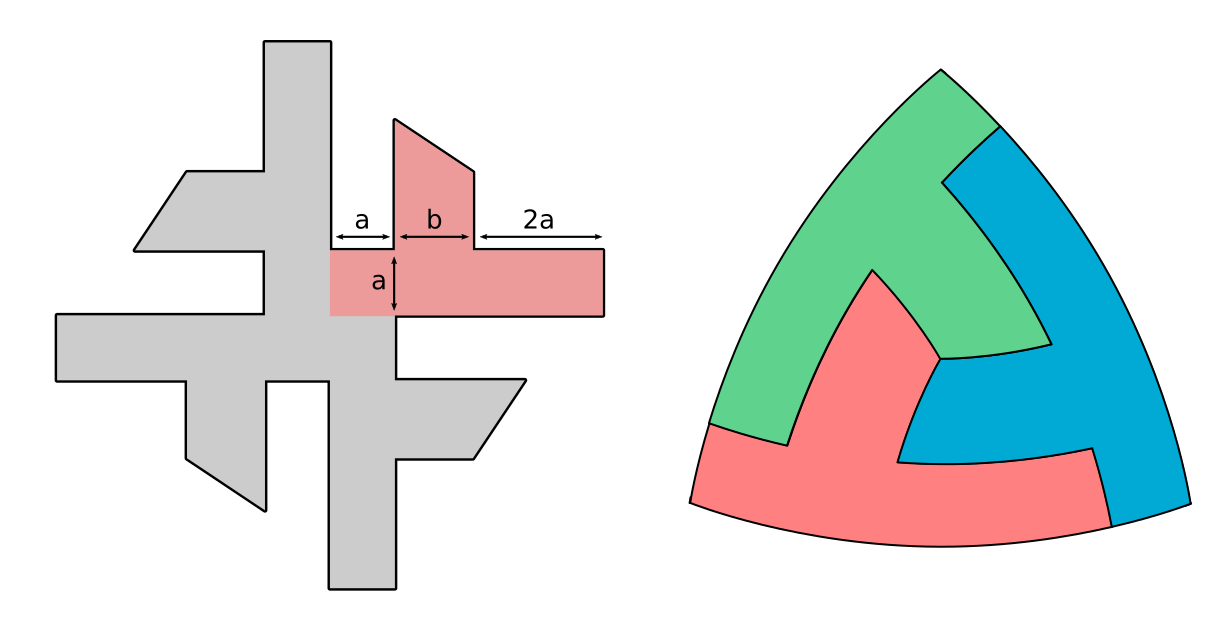
Ész Ventura: Mi az a focivébés kérdés, amire semmilyen sportújságban nem fogsz választ találni?
Már a labda sem a régi: a hagyományos csonka ikozaédert mindenféle görbült idomok váltották. Mi folyik Oroszországban?
Szorít az idő? Segít a koordinátageometria!
A kulcs a koordinátageometria, aminek a segítségével még az is meg tud oldani geometriai problémákat – legyen szó akár síkbeli akár térbeli problémákról – akinek nincs jó geometriai érzéke vagy térlátása. A koordinátageometria ugyanis a geometriai objektumokat egy önkényesen választott koordinátarendszerben koordinátaszámokkal jellemezhető algebrai struktúrákká képezi, ezáltal a probléma teljes mértékben algebrai számítássá válik.
Emlékszem, középiskolában még gyakran kaptunk olyan geometriapéldákat, hogy valamit körzővel és vonalzóval kellett megszerkeszteni. Ha nem volt esetleg otthon elég időm geometriai intuíció útján szerkesztési eljárást találni egy nehezebb geometria házira, akkor az óra előtti szünetben a koordinátageometria segítségével gyorsan meg lehetett oldani a problémát. Szerkesztés helyett ugyanis elég volt kiszámolni a szerkesztendő dolog meghatározásához szükséges paramétereket (például távolságokat), és ha a kapott képletben csak az alapműveletek szerepeltek és gyökvonás, akkor már készen is voltam, hiszen ezek a műveletek körzővel és vonalzóval elvégezhetők.
Sőt pontosan az ilyen műveletek által kapható számok, illetve hosszúságok szerkeszthetők körzővel és vonalzóval, tehát előre lehetett tudni, hogy a számítás eredménye biztosan ilyen lesz, hacsak nem adott fel a tanár megoldhatatlan problémát, mint amilyenek a híres ókori problémák, a szögharmadolás, a kockakettőzés vagy a kör négyszögesítése, amikről ma már tudjuk, hogy körzővel és vonalzóval nem megoldhatók.

No de térjünk vissza a focilabdához, ahol szerkesztenünk nem kell, csak számolni. A számításokat J3L 2404 álnevű lelkes beküldőnk megoldása alapján közöljük. A koordinátageometriai számításoknak egy nagy trükkjük van: azon koordinátarendszer jó érzékkel való megválasztása, amiben a számítások a legegyszerűbbek.
Jelen esetben nincs nehéz dolgunk, mert a panelszerkezet eleve jól illeszkedik egy derékszögű koordinátarendszerhez, melynek origóját nyilván a labda középpontjába vesszük fel. A tengelyek pedig menjenek át a feladat kitűzésekor is illusztrált nyolcad gömbfelület három sarkán az alábbi ábrán is látható módon.
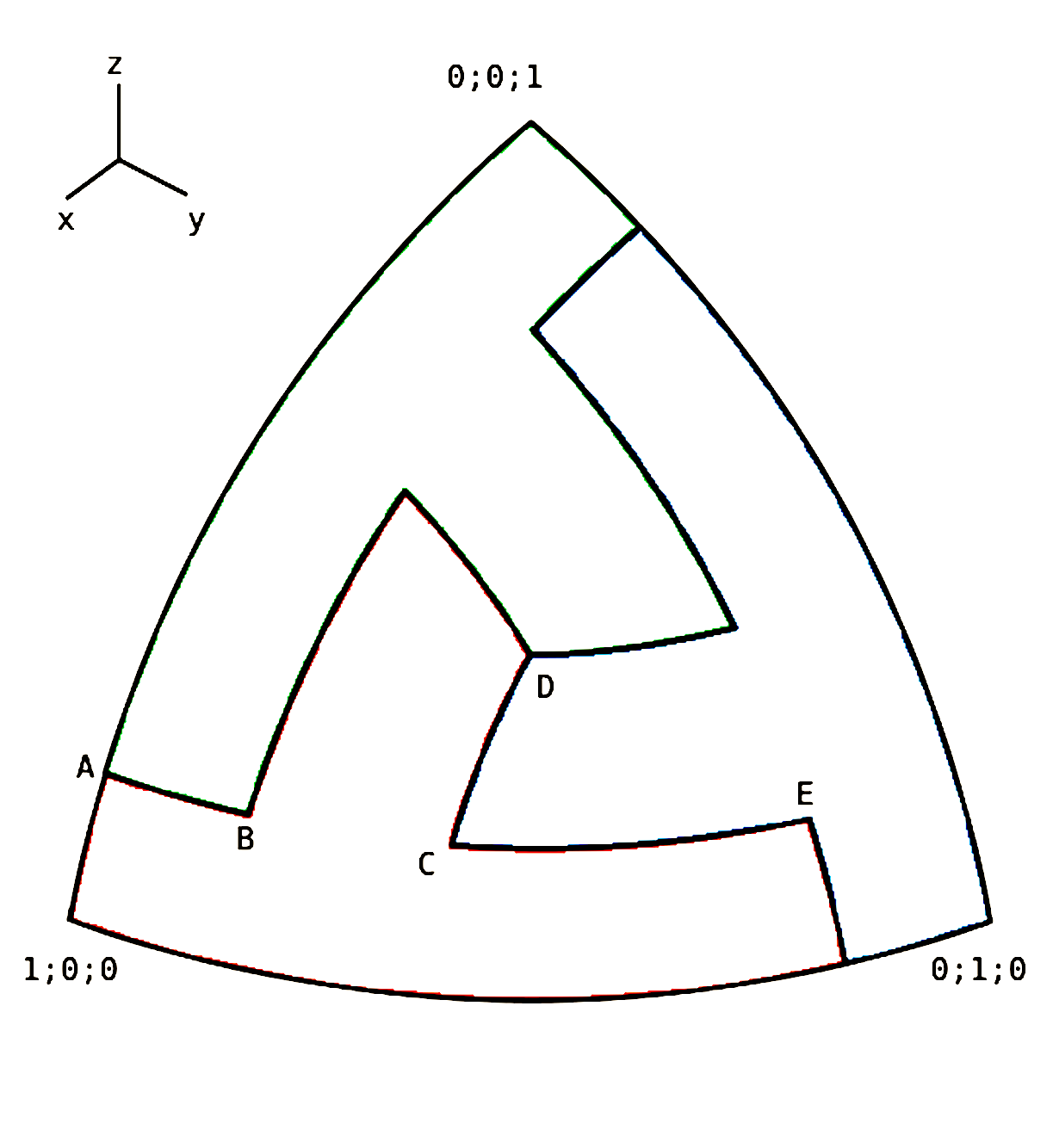
A focilabda sugara legyen egységnyi. Ekkor a labda gömbfelszínének minden pontjára teljesül, hogy három (x, y és z) térbeli Descartes-féle koordinátájának négyzetösszege, ami épp a sugár négyzete, jelen esetben egységnyi. Ez az összefüggés az ábrán bejelölt összes pontra (A, B, C, D, E) fenn fog állni. Például a D-vel jelölt pont koordinátái a panelek egybevágóságából következő forgásszimmetria miatt azonosak, értékük pedig 1/sqrt(3), hogy négyzeteik összege 1 legyen. A továbbiakban sqrt(akármi) az akármi gyökét fogja jelölni. A pontok koordinátákkal való meghatározására pedig a azt a jelölést használjuk, hogy a pont neve mögött zárójelben egymástól elválasztva felsoroljuk a koordinátákat x, y, z sorrendben: D(1/sqrt(3); 1/sqrt(3); 1/sqrt(3)).
Vegyük észre, hogy az A, B, C és E pontok mindegyike az x-y-síkkal párhuzamos síkon (vagy körön) van, azaz z-koordinátája mindegyiknek azonos, ezt jelöljük m-el. Az A pontnak az y-koordinátája zérus, mert az A pont az x és z tengelyek által kifeszített síkon helyezkedik el, a fenti négyzetösszeg kritérium alapján tehát az A koordinátáit is megadhatjuk m segítségével kifejezve: A(sqrt(1-m^2); 0; m). A B pont y-koordinátája a panelek egybevágósága miatt szintén m, x-koordinátája pedig a négyzetösszeg kritérium alapján megint számolható: B(sqrt(1-2m^2); m; m).
A C pont ugyanazon y = 1/sqrt(3) egyenlettel meghatározott síkon helyezkedik el, mint a D pont, x-koordinátája pedig a négyzetösszeg kritérium alapján számolható: C(sqrt(2/3-m^2); 1/sqrt(3); m). Végül az E pont a B ponthoz hasonló, csak fel vannak cserélve a koordinátái: E(m; sqrt(1-2m^2); m).
Nekünk a z = m összefüggés által megadott síkban lévő kör ívhosszait kell összehasonlítanunk. Az ívhosszok pedig arányosak a (0|0|m) pontból az ívhosszak végpontjaiba mutató vektorok által közbezárt szöggel, melynek a koszinusza például a szóban forgó vektorok skalárszorzatának segítségével számolható. A szóban forgó kör sugara sqrt(1-m^2). Az AB, CE és BC ívhosszakhoz tartozó szögek koszinuszaira, némi algebrai számítás után, rendre az alábbiak adódnak: sqrt(1-2m^2) / sqrt(1-m^2), (m*sqrt(2/3-m^2) + sqrt((1-2m^2)/3) ) / (1-m^2) és (sqrt(1-2m^2) sqrt(2/3-m^2) + m/sqrt(3)) / (1-m^2).
Az alapfeladat szerint a CE ívhossz az AB ívhossz duplája, amiből az ívhosszakhoz tartozó szögek koszinuszaira adódik egy feltétel, amit a trigonometrikus azonosságok (addiciós tétel) segítségével az alábbi alakban írhatunk: cos(ɣ) = 2*cos^2(α)-1, ahol α az AB ívhez tartozó szög, ɣ pedig a CE ívhez tartozó szög. Ebbe az egyenletbe behelyettesítve a korábban kapott képleteinket, m2-re egy negyedfokú egyenlet adódik, melynek megoldása m = (sqrt(6)-1)/5, közelítőleg 0.2898. Ezt visszahelyettesítve és véve a szögek koszinuszaira vonatkozó képletek arkuszát, majd azok arányait, megkaphatjuk az ívek keresett b/a arányát, amire közelítőleg 1.1043 adódik.
A haladóknak kitűzött feladat esetében az AB ívhossz a BC ívhosszal egyezik meg, így a hozzájuk tartozó szögek és azok koszinuszai is azonosak. Ennek megoldása m=sqrt((13-sqrt(73))/3)/4, kozelítőleg 0.3047. Amit visszahelyettesítve az adódik, hogy a CE ívnek az AB 1.824-szeresének kéne lennie, hogy a labda BC csíkja az AB csíkkal azonos széles legyen.
Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus, bűvész. Az Ész Ventura összes feladványa és megoldása itt olvasható.