Az Európai Leány Matematikai Diákolimpia (EGMO) 2019-es évi második feladatára négy jó megoldás érkezett a Qubit olvasóitól, ezek közül Ligeti Gábor bizonyítását közöljük, és megoldásának alapos volta miatt ő kapja a jutalomkönyvet, Peter Wohlleben A fák titkos élete című slágerkötetét.

Tökéletes megoldást küldött még be Boros Péter és Pásztor Szilárd is, Zolnai Ákos pedig helyesen oldotta meg a feladatot 8x8-as táblára, és helyes sejtést közölt a megoldás általános formájára.

Köszönjük a beküldéseket, a megfejtőknek gratulálunk!

A megoldás röviden:

A 2n x 2n-es táblát legfeljebb n(n+1)/2 dominóval lehet lefedni, és ez a lefedés mindig lehetséges is. Az n(n+1)/2 számot az n-edik háromszögszámnak nevezzük. Ezeknek a számoknak az a tulajdonságuk, hogy az n-edik és n-1-edik háromszögszám különbsége mindig n. Amikor pedig a feladatban a táblánkat 2(n-1) x 2(n-1)-es oldalúról 2n x 2n -esre bővítjük, akkor az eddig letett dominókhoz még n-et tudunk hozzátenni a lefedési szabály betartásával: így kapjuk meg, hogy a dominók maximális száma a 2n x 2x-es táblán az n-edik háromszögszám. Ezt bizonyítja be ötletesen Ligeti Gábor.

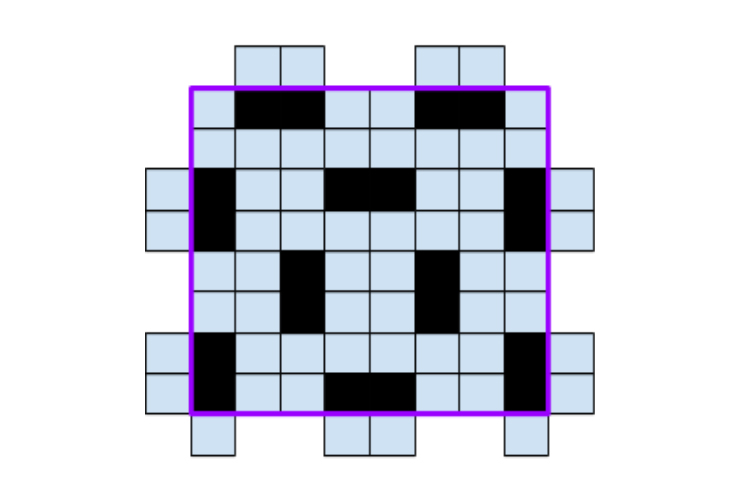
8x8-as táblára legfeljebb 10 dominót lehet elhelyezni, és az alábbiakban mutatunk is egy megfelelő elhelyezést.

Emlékeztetőül álljon itt a kitűzött feladat:

Legyen n bármilyen pozitív egész szám (n=1,2,3 …), és vegyünk egy 2n x 2n nagyságú, négyzet alakú táblát. A táblára úgy akarunk néhány dominót lehelyezni, hogy a tábla minden mezőjének pontosan 1 dominóval fedett szomszédja legyen. A tábla két négyzetét szomszédosnak hívjuk, ha nem egyeznek meg, de van közös oldaluk.

A dominó egy 2x1-es vagy 1x2-es téglalap, amiket úgy teszünk le, hogy egymást semelyik négyzeten se fedjék.

Határozzuk meg n függvényében, minden n-re, hogy hány dominó rakható le legfeljebb a fenti módon a 2n x 2n-es táblára!

Ligeti Gábor megoldása pedig a következő:

Legyen a tábla oldala m=2n. 

Először is lássuk meg, hogy minden dominónak van egy 6 négyzetből álló “környezete”, amik maga a dominó két négyzetével együtt azok a négyzetek, amiknek épp ez a dominó az egyetlen “dominószomszédja”. Legyen a dominó fekete, a “környezet” világoskék -- ekkor egy ilyen alakzatot kapunk:

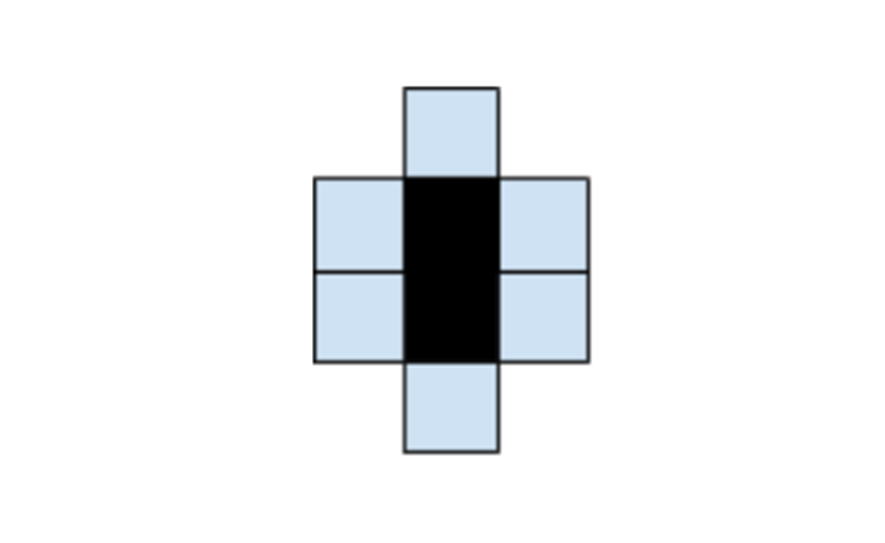
A feladat tehát kicsempézni a táblát úgy, hogy

• dominók (fekete rész) csak a táblán belül lehetnek teljes terjedelmükben

• a tábla belsejét tökéletesen, átfedés nélkül lefedjük ezekkel az alakzatokkal.

Látható, hogy a kék rész kilóghat a táblából, de a táblán belül mindent le kell fednünk (hiszen dominószomszédja csak magának a dominónak, vagy a környezete négyzetének van). Átfedés esetén az átfedett négyzetnek két dominószomszédja is lenne, ezért átfedés nem lehet. Ahhoz, hogy a táblán belül minden négyzetnek pontosan egy dominószomszédja legyen tökéletes, átfedés nélküli tökéletes kicsempézés kell. 

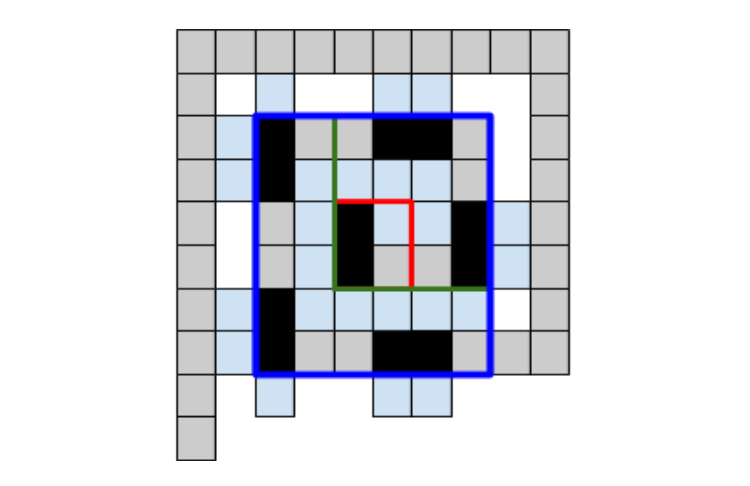
Vizsgáljuk meg, mennyi kék négyzet lóghat ki a táblából!

Vegyük észre, hogy ilyen túllógás kizárólag a táblával szomszédos m=2n hosszú sorokban/oszlopokban lehetséges. Az alakzat formája miatt vagy egy, vagy két négyzet lóghat túl egy-egy alakzatból, amit utána két üres négyzet kell, hogy kövessen. Mivel a sort kezdhetjük is, és zárhatjuk is két-két kék kockával, ez minden sorban/oszlopban maximálisan n+1 kék kockát jelenthet. 

Ha k dominóval fedjük le a feltételek szerint az m=2n oldalú táblát, akkor a fentiek miatt ezek az alakzatok összesen 8k négyzetet (fekete+kék) fednek le, ebből a táblán belül m²=4n² négyzet található, a kilógással együtt pedig maximum m²+4(n+1)=4n²+4n+4 négyzetet boríthat be.

4n² ≤ 8k ≤ 4n²+4n+4

ebből

k ≤ (n²+n+1)/2=n(n+1)/2 + 1/2

mivel k egész szám, és n(n+1)/2 is egész (hiszen n és n+1 egyike páros), az 1/2 elhagyható, a feltétel tehát

k ≤ n(n+1)/2

Lássuk most be, hogy ilyen lefedés van is. 

Tekintsük a következő lefedést n=1,2,3 esetekre:

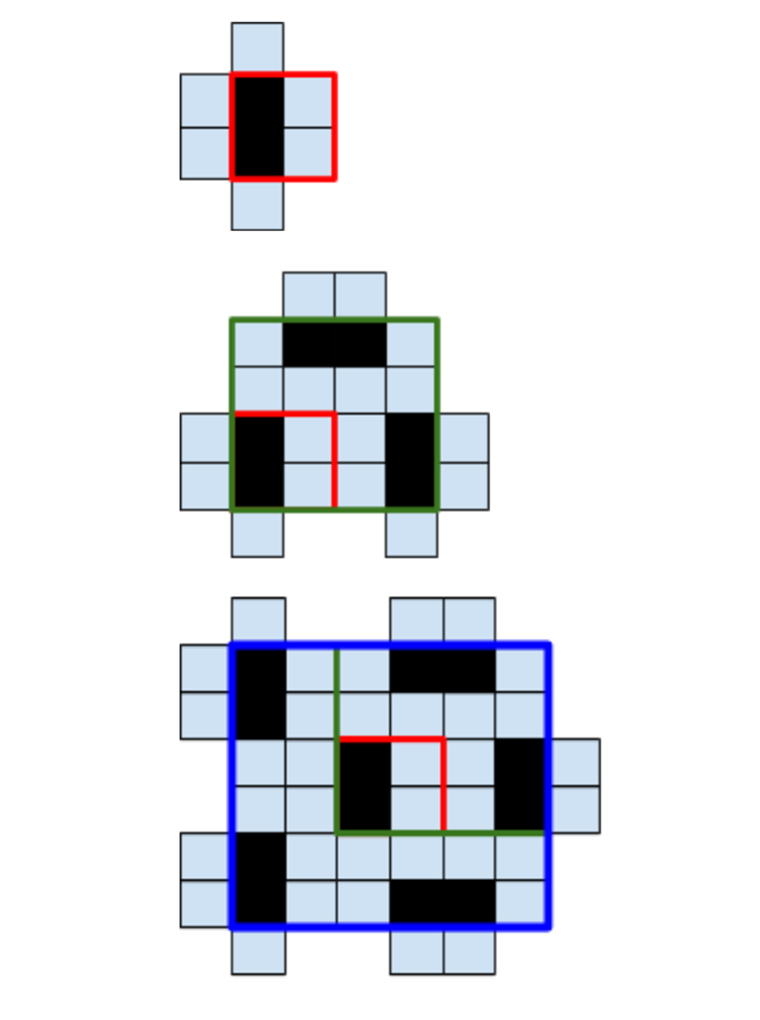
Könnyen belátható, hogy ez a lefedés csigavonal mentén tetszőlegesen tovább folytatható:

A lefedés a csigavonal mentén rendre 1,2,3,4,...,n újabb alakzattal bővíthető, így épp n(n+1)/2 dominóból áll, ami a maximális darabszám.

Az a feladatban megadott 8x8-as tábla esetén m=2n=8, n=4, tehát 10 dominó helyezhető el a feltételeknek megfelelően.