A négy részre tört pálca című feladványban az volt a kérdés, hogy mi a valószínűsége annak, hogy egy véletlenszerűen négy részre tört pálca darabjaiból kirakható egy háromszög. A bónusz kérdés az volt, hogy hány részre kell törni a pálcát, hogy a darabokból biztosan ki tudjunk választani hármat úgy, hogy azokból háromszöget tudjunk alkotni.

Kezdjük a bónusz kérdéssel, ami kivételesen egyszerűbb. A válasz az, hogy előfordulhat olyan végtelen törési sorozat, hogy végtelen sok darabból sem tudunk hármat úgy kiválasztani, hogy háromszöget alkossanak. Mint ismeretes, a háromszög létezésének feltétele, hogy a két rövidebb oldal összege nagyobb legyen, mint a harmadik oldal. Ha mondjuk a pálcából letört legnagyobb darab hosszabb, mint a pálca fele, és a második legnagyobb darab hosszabb, mint a maradék fele, és így tovább, akkor ezekből a darabokból sosem tudunk háromszöget alkotni, még akkor sem, ha végtelen sokáig törögetünk, hiszen bármely három darabból a leghosszabb mindig hosszabb lesz, mint a másik kettő együtt.

Most nézzük annak a valószínűségét, hogy a négy részre tört pálca esetén valamely három darabból kirakható egy háromszög. A legegyszerűbb természetesen az, ha az ember szimulálja a folyamatot számítógépen. Nem kell mást tenni, mint generálni három véletlenszerű töréspontot a pálcán, amit a feladat szerint egyenletes eloszlásból kell vennünk a pálca mentén. Legyen a pálca egységnyi hosszú, a töréspontoknak a pálca egyik végétől vett távolsága pedig legyen növekvő sorrendben x, y és z. Ez esetben a kapott darabok hossza: x, y-x, z-y, 1-z. A kapott négy szakaszból négyféleképpen lehet hármat kiválasztani, és a számítógép könnyedén ellenőrizheti, hogy valamelyik kombinációra teljesül-e a háromszögek szerkeszthetőségi feltétele, miszerint a két rövidebb oldal összege nagyobb, mint a harmadik oldal. Mármost a számítógépnek beprogramozhatjuk, hogy ezt ismételje meg nagyon sokszor (N-szer), és mondja meg nekünk, hogy az esetek hányad részében lehet háromszöget szerkeszteni.

Mindezt egy személyi számítógép pár másodperc alatt kiszámolja, és a végeredmény 0,571 körüli érték lesz. Ez természetesen szimulációról szimulációra változhat, de ha N-et elég nagyra választjuk, és azt tapasztaljuk, hogy különböző N-es szimulációk esetén a harmadik tizedesjegyig minden számjegy ugyanaz, akkor nagy valószínűséggel három tizedesjegyre pontos az így kapott becslésünk. Ezt a módszert nevezzük Monte Carlo szimulációnak, amivel egy számítógép segítségével lényegében megmértük a valószínűséget. A mérési eredmény azonban nem egy egzakt megoldás, csak egy nagyon jó közelítő érték a keresett valószínűségre.

Hogyan lehetne egzaktul kiszámolni a valószínűséget? Ehhez térjünk vissza a töréspontok kiválasztásához. A töréspontokat továbbra is x, y és z értékekkel jellemezzük, amik a pálca egyik végétől vett távolságok, de most ne követeljük meg közöttük a növekvő sorrendet. x, y és z tehát egyenletesen választott véletlen számok a [0,1] intervallumból. Ez nagyon szerencsés, mert gondolhatunk úgy erre a három számra, mint térbeli koordinátákra, vagyis az (x,y,z) hármas megad egy térbeli pontot egy egység oldalú kockában. Mivel mindegyik koordinátát egymástól függetlenül egyenletes eloszlásból választjuk, ezért tekinthetjük úgy a három darab véletlen törést, mint egy darab térbeli pont véletlenszerű kiválasztását az egységkockában. Ha a pálcát öt részre törnénk, akkor most gondolkodhatnánk négy dimenzióban.

Lesznek olyan pontok, azaz (x,y,z) hármasok az egységkockában, amikre szerkeszthető háromszög az x, y-x, z-y, 1-z szakaszok felhasználásával, és lesznek olyan pontok, amiknél ez nem lehetséges. Feltehetőleg azon pontok halmaza, amire szerkeszthető háromszög, valami összefüggő poliédert alkot a kockán belül, és ennek a térfogata fogja megadni, hogy mekkora a valószínűsége annak, hogy ebből a halmazból választunk. A térfogatot a kocka teljes térfogatához kell viszonyítanunk, de mivel ez az utóbbi éppen egységnyi, ezért a kérdéses térfogat éppen a kérdéses valószínűséget fogja megadni.

Természetesen x, y és z nagyság szerinti sorrendje hatféle lehet, és a szimmetria miatt ezen sorrendek valószínűsége teljesen azonos. Így elég egy ilyen sorrendet vizsgálni, vagyis újra feltehetjük, hogy 0 < x < y < z < 1. Ekkor a négy pálcadarab hossza x, y-x, z-y és 1-z, és ezekből hármat négyféleképpen tudunk kiválasztani.

Ha például az x, y-x, és z-y szakaszokból szeretnénk háromszöget szerkeszteni, akkor az alábbi háromszög-egyenlőtlenségeknek kell teljesülniük:

x + (y-x) > z-y
x + (z-y) > y-x
(y-x) + (z-y) > x

Hasonlóan megadhatjuk a teljesítendő egyenlőtlenségeket a másik három esetben is. Bármely esetre felírt egyenlőtlenségek mindegyikére igaz, hogy ezek lineárisak lesznek x-ben y-ban és z-ben, ami azt jelenti, hogy mindegyik egy síknak felel meg, és az egyenlőtlenséget kielégítő pontok halmaza a sík egyik oldala, azaz egy (nyílt) féltér. Ha ezekhez még hozzávesszük a 0 < x < y < z < 1 feltételt is, akkor az egyes esetekben az háromszög-egyenlőtlenségekhez tartozó három féltér és a fenti egyenlőtlenséget kielégítő hatod kocka metszete adja a feltételeknek megfelelő pontok halmazát, ami mindenképpen egy síkokkal határolt poliéder.

Mivel minket az érdekel, hogy valamely hármasból szerkeszthető-e háromszög, ezért a fenti négy esethez külön-külön meghatározott feltételeknek megfelelő ponthalmazoknak az együttesét (únióját) kell vennünk, és annak a térfogata fogja megadni a keresett valószínűség hatodát.

Ha valakinek nincsen térlátása, akkor itt a következő trükköt alkalmazhatja, amit Boros Péter megoldónk is használt, akitől az alábbi szemléltető animáció származik. Rögzített x esetén nézzük meg, hogy milyen y és z értékekre teljesülnek a feltételek. Ezt besatírozva az y-z síkon, a keresett poliédernek egy metszetét fogjuk kapni. Az alábbi animáción láthatjuk, hogy a négyféle esethez tartozó halmaz hogyan változik, mindegyik más színnel van határolva.

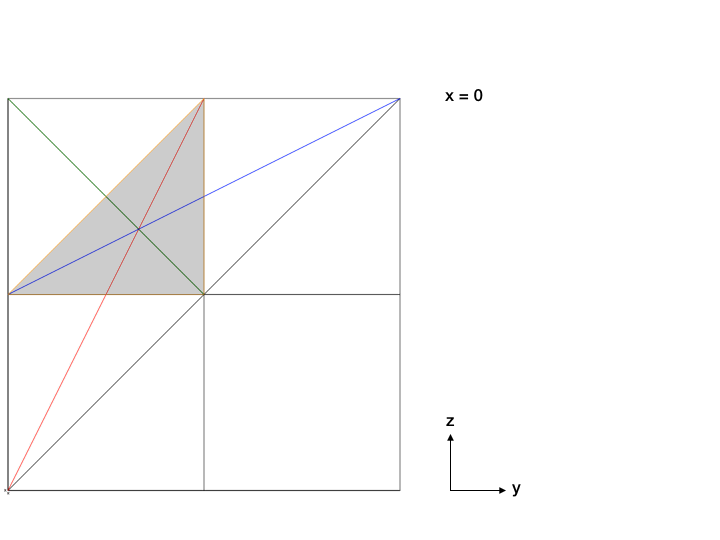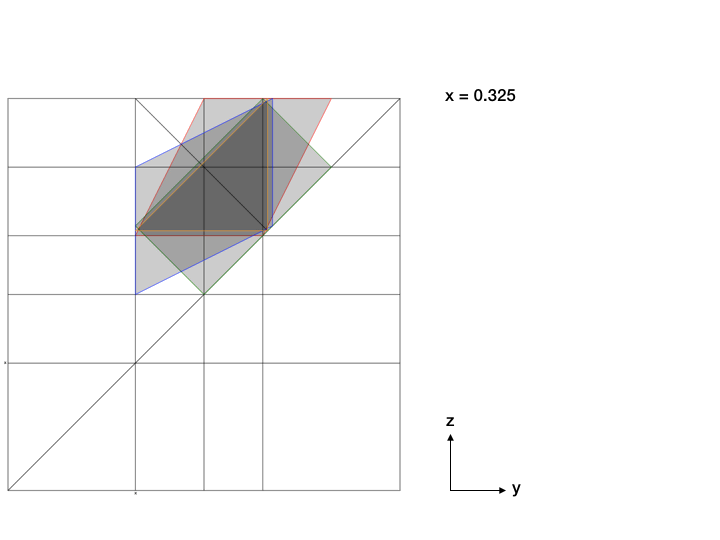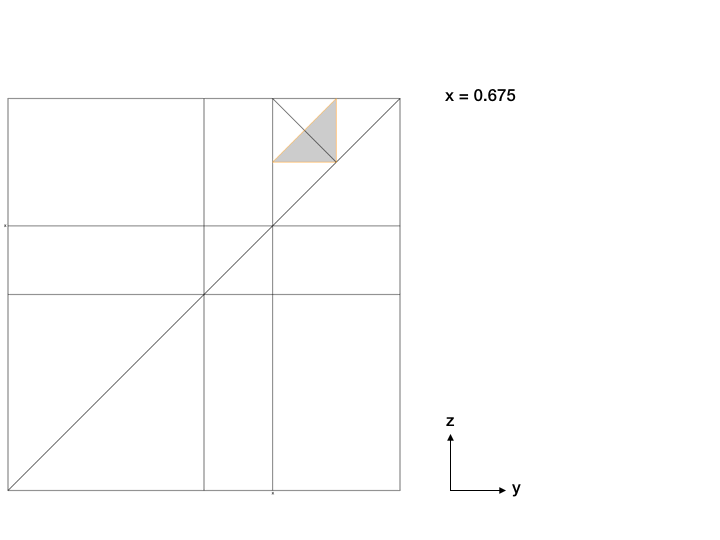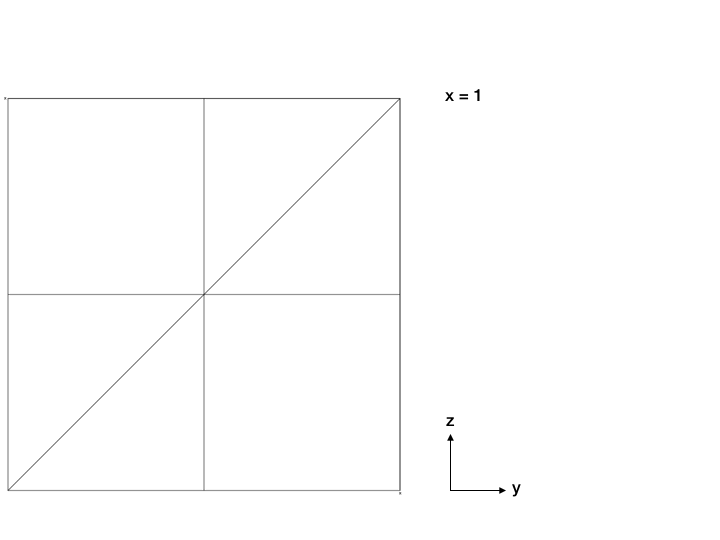
Ha most a fenti metszetsorozatú poliéder térfogatát szeretnénk kiszámolni, akkor x szerint több tartományt érdemes különválasztani, mert van, ahol a metszet konkáv, de például x = 1/4-nél konvex hatszöggé válik, aztán x = 1/2 fölött pedig végig derékszögű háromszög, vagyis ott csak egy háromszög alapú gúla térfogatát kell kiszámolnunk. Ha viszont valaki nem akarja gúlákból kirakni ezt a poliédert darabonként, akkor az integrálás segítségével is megoldhatja, ha ugyanis adott x-re f(x) a feltételeknek eleget tevő szürkére színezett rész területe, akkor a térfogat ennek x szerinti integrálja lesz x = 0-tól 1-ig. Csak a végén ne felejtsük el az eredményt hattal szorozni, hiszen feltettük, hogy 0 < x < y < z < 1. Érdekes módon a végeredmény nagyon egyszerű alakot ölt majd, a keresett valószínűség ugyanis 4/7-ed lesz.

További érdekesség, hogy ez a valószínűség kiszámolható zárt alakban általánosabb esetben is, amikor a pálcát tetszőleges számú darabra törjük, és az eredményben a Fibonacci-számok jelennek meg.