A megkeseredett WC-burkoló burkolási problémájában az volt a kérdés, hogy hány különböző módon lehet leburkolni az 1 négyzetméter alapterületű mellékhelységet 20 cm és 40 cm oldalélű négyzet alakú padlólapokkal, vagyis hány napig dolgozik még a munkáját megunt WC-burkoló.

Legyen a kisebb padlólap egységnyi élű. Ekkor az a kérdés, hogy egy 5x5-ös négyzetet hányféleképpen lehet lefedni hézag- és átfedésmentesen 1x1-es és 2x2-es csempéket használva. A feladatot általános 5xn-es helységre oldjuk meg Dévai Gergely megoldónk által felírt rekurziós összefüggések segítségével. A még általánosabb nxm lefedések száma egyébként ismert az irodalomból is (Mathar, 2016).

Jelölje f(n) az 5xn méretű padló lefedéseinek számát, és próbáljunk meg rekurziós képletet felírni f(n)-re. Három eset van:

(1) Azok az lefedések, amelykben az n-edik sor csupa kis csempéből áll, megfeleltethetők az 5x(n-1) méretű padló lefedéseinek, vagyis ezek száma f(n-1).

(2) Azok a lefedések, amelyeknek az n-edik (legalsó) sora két nagy csempét is tartalmaz (pontosabban mindkettőnek a felét), három csoportba oszthatók a nagy csempék elhelyezkedése szerint, lásd az alábbi ábra fölső sorát. Bármelyik kombináció esetén igaz az, hogy az (n-1)-edik sorban már csak egy kis csempe fér el a két nagy mellett, ezért a lefedések mindhárom esetben megfeleltethetők az 5x(n-2)-es lefedéseknek. Az utolsó sorban (a szaggatott vonal alatt) két nagy csempét is részben tartalmazó lefedések száma tehát összesen 3·f(n-2) lesz.

(3) Vannak még azok a lefedések, amelyekben az n-edik (legalsó) sorban pontosan egy nagy csempe (fele) található. Ebben az esetben a nagy csempe négy féle pozícióban lehet, lásd az alábbi ábra alsó sorát. Ha a nagy csempe az egyik szélen van, akkor a lefedések száma legyen g(n-1). A szimmetria miatt mindegy, hogy melyik szélen van. Ha valamelyik középső pozícióban, akkor az ehhez tartozó lefedések száma legyen h(n-1). g(n) tehát annak a száma, hogy hányféleképpen csempézhatő le egy olyan 5xn-be beleférő terület, aminek az alsó széle olyan alakú, mint a bal alsó mintázat fölső széle, h(n) pedig ugyanez a mellette lévő mintázatra vonatkoztatva. Összességében tehát az ebbe a kategóriába eső, azaz a szaggatott vonal alatt pontosan egy nagy csempe felét tartalmazó 5xn-es lefedések száma 2·g(n-1) + 2·h(n-1) lesz.

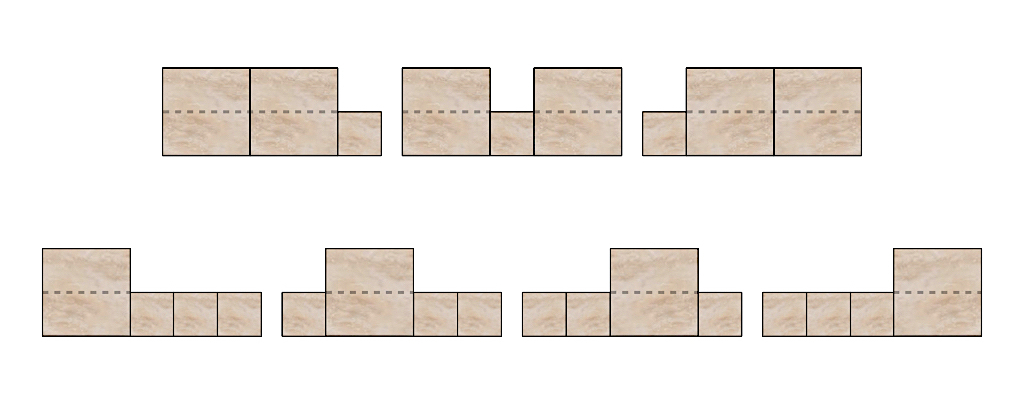
Azt kaptuk tehát, hogy f(n) = f(n-1) + 3·f(n-2) + 2·g(n-1) + 2·h(n-1). A minket érdeklő f(n) függvényen kívül viszont bevezettünk két másikat: g(n)-t és h(n)-t, ezért most azokra is fel kell még írnunk rekurziós összefüggéseket.

Ha megnézzük, hogy az utolsó két sorban elhelyezkedő nagy csempe milyen pozíciókban enged meg egy másik nagy csempét az utolsó előtti sorban, akkor az alábbi rekurziós összefüggéseket írhatjuk még fel: g(n) = f(n-1) + g(n-1) + h(n-1), illetve h(n) = f(n-1) + g(n-1), ahol az f-es tagok annak felelnek meg, hogy a szóban forgó nagy csempe soraiban nincsen másik nagy csempe.

Ha most megnézzük mi a helyzet akkor, ha csak egy vagy két sor van, akkor megállapíthatjuk, hogy f(1) = 1, f(2) = 8, g(1) = 1, g(2) = 3, h(1) = 1, h(2) = 2. Ezek után pedig már használhatjuk a rekurziós összefüggéseket, amiből némi számolás után az fog adódni, hogy f(5) = 314, illetve f(10) = 221799. A WC-burkoló tehát egy évnél kevesebbet kell még dolgozzon, de a haladó kérdés esetében ez már emberöltőnél is több.