Képakasztás öt szegre című feladványunkban az volt a feladat, hogy egyetlen madzaggal akasszunk fel egy képet öt egymás melletti szögre úgy, hogy bármelyik szöget húzzuk ki a falból, a kép a kihúzott szögtől balra lévő szögeken akadjon fenn. Ha tehát az első szöget húzzuk ki, akkor essen le a kép a falról, de ha a második szöget húzzuk ki, akkor maradjon a kép a falon úgy, hogy csak az első szög tartja. Ha a harmadik szöget húzzuk ki, akkor a képet az első két szög tartsa meg, és így tovább. A madzagot nem volt szabad elvágni, nem volt megengedett önmagával csomózni, csak a két végét lehetett a képkerethez kötni, a köztes résznek pedig a szögek között kellett tekergőznie.

Úgy tűnhet, hogy nehéz hozzányúlni a feladathoz, amely határozottan geometriai, sőt topológiai problémának tűnik, de ha meghallgatjuk A lány nem lyukára akasztott háromkezű fiú című kocsmavideót Pintér Gergő matematikustól, amit segítségként megadtunk, akkor kiderül, hogy valójában a kép felakasztásánál alkalmazott kötélgubanc algebrai kifejezésnek vagy egy betűsorozatnak, azaz szónak is tekinthető, és rajzolás nélkül is tudunk megoldást konstruálni a feladatra. A másik segítség természetesen az, hogy kezdjük először csak két szöggel, és nézzük meg a konstrukciónkat, hogyan tudnánk növelni benne a szögek számát.

Legyen tehát két szög, a bal oldalit nevezzük A szögnek, a jobb oldalit B szögnek. A feladatunk tehát az, hogy amennyiben az A szöget húzzuk ki, essen le a kép a falról, ha viszont a B szöget húzzuk ki, akkor maradjon lógva, azaz valamilyen módon tartsa meg az A szög a képet. Egy lehetséges megoldást mutat az alábbi ábra.

A kötél által formált gubanc az alábbi módon tekinthető egy szónak. Induljunk el a kötél egyik végétől (lásd a nyilat a fenti képen) a kötél mentén, és nézzük meg, hogy a kötél rendre mely szögeket és milyen irányból kerüli meg. Ha az A szöget kerüli meg az óramutató járásával megegyezően, akkor leírunk egy A betűt, ha a B szöget, akkor leírunk egy B betűt. Ha az óramutató járásával ellentétesen kerülünk meg egy szöget, akkor A' és B' jeleket írunk. Ezeket a jeleket leírjuk egymás után balról jobbra, ahogy a kötél mentén rendre elhaladunk a szögek mellett, bármelyik szöget akár többször is megkerülve. Mire a kötél másik végéhez érünk, leírunk egy szót, amely az A, A', B, B' jelekből áll. A fenti megoldáshoz tartozó szó például B'AB lesz.

Ha kihúzunk egy szöget, az annak felel meg, hogy a szóból kihúzzuk a szöghöz tartozó összes betűt és a vesszős alakját is. Ha tehát a B'AB szóból kihúzzuk a B-ket, akkor egy A marad, vagyis a kép lógva marad az A szögön. Ha viszont kihúzzuk az A-t, akkor B'B marad, ami viszont nem számít huroknak, lényegében semmivé redukálódik. Ha ugyanis a kötéllel megkerüljük a B szöget az egyik irányba, majd ellentétes irányba is megkerüljük, azaz visszafordulunk ugyanazon az úton, és húzzuk magunk után a kötelet, akkor az olyan, mintha meg se kerültük volna. Amikor tehát egy betű és annak a vesszős alakja egymás mellé kerül, akkor a két betűt kihúzhatjuk a szóból, tekinthetjük úgy, mintha ott se lenne.

Ezt a megoldást könnyen általánosíthatjuk. Legyen egy harmadik C szög, ami legyen a B után a jobb szélen. Ekkor a megoldás lehet ez: C'B'CAC'BC. Ha ebből kihúzzuk az A-t, akkor marad C'B'CC'BC = C'B'BC = C'C = semmi. Ha a B-ket húzzuk ki, akkor marad C'CAC'C = A. Ha pedig a C-ket húzzuk ki, akkor marad B'AB, vagyis a B és A szögeken marad lógva a kép. Épp ezt akartuk.

Hasonló módon mehetünk tovább, tehát amikor veszünk még egy szöget, akkor csak az előző szóban körbevesszük az eddigi leginkább jobbra lévő szöghöz tartozó betűket az új betű vesszős és vesszőtlen verzióival. Az öt szöges megoldás tehát az alábbi lesz: E'D'E C' E'DE B' E'D'E C E'DE A E'D'E C' E'DE B E'D'E C E'DE. Annak pedig, aki látni is szeretné, hogy néz ki, Szentesi Balázs megoldónk jóvoltából alább meg is tekintheti.

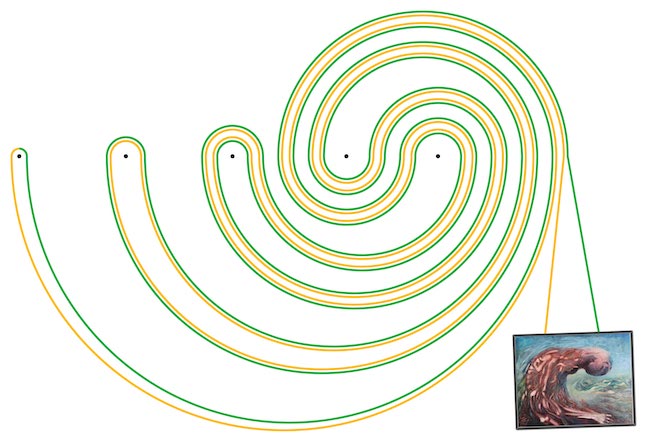
Kapcsolódó cikk a Qubiten: