Ész Ventura: Okosabb vagy, mint egy amerikai gimnazista 1982-ből?

Régóta kering az interneten egy feladvány, ami különböző fórumokon újra és újra parázs viták tárgyát képezi. A feladat eredetileg 1982-ből egy amerikai érettséginek megfelelő vizsga (SAT teszt) feladatsorából származik, és egyszerű matekpéldának szánták, de azáltal, hogy nem volt kellően körültekintő a megfogalmazása, valójában fizika példának is tekinthető, ugyanis a forgás, fordulás, fordulat szavak definícióját érinti.
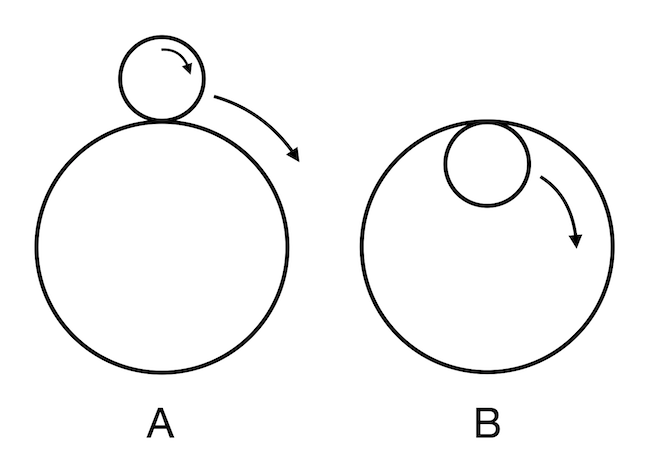
A feladat szerint van két kör, amelyek közül a kisebbik 1 egység sugarú, a nagyobbik pedig 3 egység sugarú. A kis kör csúszásmentesen végiggördül a nagy körön, lásd az alábbi illusztráción az A-val jelölt bal oldali ábrát. Hány fordulatot tesz meg a kis kör, míg visszaér eredeti pozíciójába a nagy körön? A hivatalos válasz 3 volt, de a sok százezer diák közül néhányan jelezték, hogy a helyes válasz szerintük nem annyi, és igazuk volt.
126. feladvány: Kör körökön
Az első kérdés ezzel a feladattal kapcsolatban, hogy mi a helyzet akkor, ha a kis kör nem kívül, hanem a B ábrán látható módon a nagy a kör belsejében gördül végig. Ugyanannyi fordulatot tesz meg, mint az A esetben, vagy sem?
A második kérdés: hány fordulatot tesz meg a kis kör, ha két egymással érintkező nagy körön gördül végig egy fekvő nyolcas mentén, ahogy az az alábbi illusztráción is látszik? A kis kör az egyik nagy körnek a külsején gördül, a másik esetében viszont belül gördül végig. A fekvő nyolcas alakú pálya esetében a pálya önmetszésétől tekintsünk el, az nem akadályozza a mozgást!
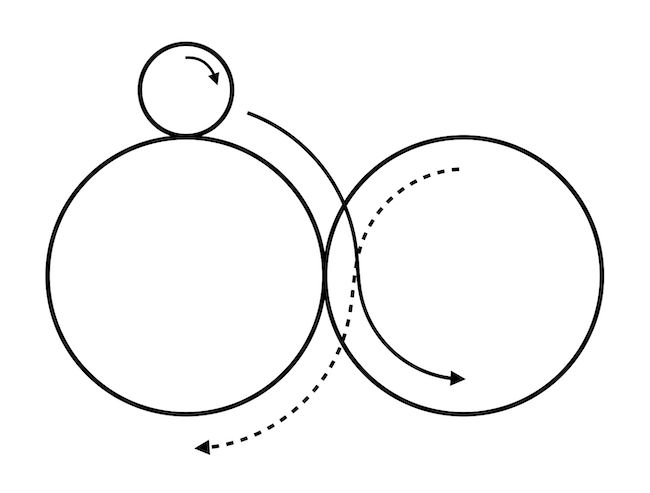
Megjegyzés: a nagy körök minden esetben rögzítettek, nem mozdulnak el.
Nehézségi szint:

A megfejtéseket magyarázattal és ábrával együtt az eszventura@qubit.hu címre várjuk. A legértékesebb megoldást küldő versenyzők felkerülnek az Ész Ventura dicsőségfalára, közöttük és minden jó megoldást beküldő versenyző között év végén nyereményeket sorsolunk ki. Az e-mail subject mezőjében kérjük sorszámmal jelezni, hogy melyik feladvány megoldásáról van szó. Beküldési határidő: augusztus 10. éjfél.
Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus és bűvész