Szerkesztés kétélű vonalzóval című feladványunkban egy kör középpontját kellett egy olyan vonalzóval megszerkeszteni, aminek két egymással párhuzamos éle van, de a vonalzó élein nincsenek rovátkák, és nem is firkálhatunk vagy karcolhatunk rá semmit, lásd az alábbi ábrát.

A Poncelet–Steiner-tétel kimondja, hogy az euklidészi szerkesztéssel (azaz körző és vonalzó használatával) megszerkeszthető pontok a síkon megkaphatók csak vonalzó használatával is, abban az esetben, ha meg van adva akárhol a síkon egyetlen tetszőleges sugarú kör, és annak a középpontját is ismerjük. Ha tehát a fenti kétélű vonalzó alkalmas arra, hogy egy kör középpontját megszerkesszük, akkor ebből az is következik, hogy euklidészi szerkesztésekhez elegendő csak egy körvonal és egy kétélű vonalzó. Amennyiben tehát otthon hagytuk az állítható körzőnket, akkor tulajdonképpen egy tetszőleges méretű bögre és egy léc segítségével is el tudunk minden euklidészi szerkesztést végezni, sőt igazából az első kör megrajzolása után a bögrét földhöz is vághatjuk.

Húrok és felező merőlegesek

Ha a kör két általános helyzetű (egymással nem párhuzamos) húrjára felező merőlegest tudunk állítani, akkor készen vagyunk, hiszen a két felezőmerőleges pont a kör középpontjában metszi egymást. Ehhez azonban először be kell húznunk a körnek egy húrját. A húr akármilyen kicsi lehet, ezért akármilyen rövid is a vonalzónk, húrt mindenképpen be tudunk húzni. Egyébként pedig arra is van lehetőség hogy a vonalzó hosszánál nagyobb húrt behúzzunk, hiszen a vonalzót tovább tudjuk tolni egy elkezdett egyenes mentén.

Ha van már egy húr, akkor többféle módon is berajzolhatjuk annak felezőmerőlegesét. Ha a húrral párhuzamosan húzunk még egy egyenest a kétélű vonalzó segítségével, és ez az egyenes is metszi a kört, akkor a két párhuzamos húr körrel való metszéspontjai egy húrtrapéz csúcsait fogják alkotni. Ezek után húzzuk be a trapéz átlóit, és hosszabbítsuk meg a trapéz ferde oldalait. Az átlók metszéspontját összekötve az oldalvonalak meghosszabbításának metszéspontjával megkapjuk a húrokra állított felezőmerőlegest, lásd az alábbi ábrát.

Ha a vonalzó elég vékony, akár húzhatunk még húrt, amely párhuzamos az előző kettővel, így két trapézt tudunk alkotni, és a két trapéz átlóinak metszéspontjait összekötve szintén megkaphatjuk a keresett felezőmerőlegest, lásd a második ábrát.

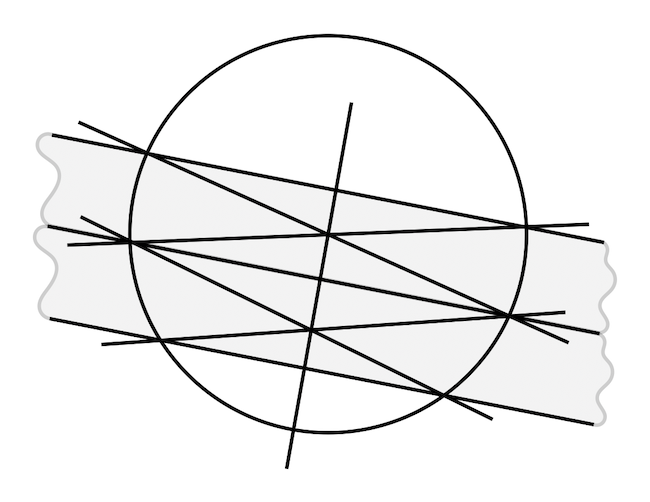
Mi okozhat problémát a szerkesztés során? Ha a vonalzónk nem elég hosszú, akkor a húrokat ugyan meg tudjuk rajzolni odébbcsúsztatással, de előfordulhat, hogy az átlós pontokat nem éri át a vonalzónk, ezért az átlókat már nem tudjuk behúzni. Ez a probléma azonban kiküszöbölhető, ha elegendően kicsi trapézt tudunk rajzolni, azaz a körnek nagyon a széléből le tudunk metszeni egy vékony csíkot. A másik probléma az lehet, ha a vonalzó túl széles, például a kör átmérőjénél is szélesebb, így az első húrral párhuzamosan felvett egyenes nem metszené a kört. Ez a probléma is kiküszöbölhető, ha tudunk tetszőlegesen keskeny csíkozást gyártani, amire például az alábbi módszer használható.

Húzzunk párhuzamos vonalakat a vonalzó szélességének megfelelő sortávolsággal, azaz csíkozzuk be a papírt. Ezután készítsünk egy másik csíkozást is, ami metszi ezeket a csíkokat, így kapunk egy torzított négyzetrácsot, amiben négyzetek helyett paralelogrammák, sőt igazából rombuszok vannak. Ha a kialakuló rombuszok átlóit meghúzzuk, majd a megfelelő metszéspontokat összekötjük, akkor az előző csíkozást meg tudjuk felezni, azaz minden szomszédos párhuzamos vonal közé be tudunk húzni még egy párhuzamos vonalat. És ezt akárhányszor megismételhetjük, azaz a csíkok távolságát felezgetve akármilyen kicsi sortávolságú csíkozást létrehozhatunk, ami előbb vagy utóbb elég sűrű lesz ahhoz, hogy a kört elmetssze és abból trapézokat metsszen ki, ami nekünk kell.

No de mi a helyzet akkor, ha a vonalzó egyszerre túl rövid és túl széles, extrém esetben úgy néz ki, ahogy az alábbi ábrán is látszik. A kedves olvasóra bízzuk, hogy ekkor meg lehet-e oldani a szerkesztést. Azok között, akik erre megoldást küldenek, különdíjat sorsolunk ki.

Végül pedig válaszoljunk az egyik bónusz kérdésre. A szerkesztés akkor is megy, ha a kétélű vonalzónk két éle nem párhuzamos egymással, hanem szöget zárnak be. Ha ugyanis a vonalzó egyik élét eltoljuk egy egyenes mentén akkor a másik él használatával egymástól tetszőlegesen kis távolságra húzhatunk párhuzamos egyeneseket, és akkor a fenti trapézos módszer működőképes marad.

Kapcsolódó cikk a Qubiten: