Tenisztaktika című feladányunkban modelleztük a tenisz egy játékát. Egy játék megnyeréséhez legalább négy labdamenetet kell nyerni, és legalább két labdamenettel többet, mint az ellenfél. A feladat szerint az egyik játékos (A) minden labdamenet előtt eldönti, hogy mindent beleadva kihajtja magát, vagy pedig lazábbra veszi a figurát. Ellenfele (B) viszont egyenletes energiabefektetéssel játszik végig. Ezt úgy modelleztük, hogy a B játékos egy nyolcoldalú dobókockával (pontosabban oktaéderrel, ún. D8) dob, míg az A játékos választhat, hogy hatoldalúval (D6) vagy tízoldalúval (D10). Miután mindketten dobtak, az A játékos a dobásából még levonja a fáradtsági szintjét. A fáradtsági szint negatív is lehet, ekkor kipihentségről beszélünk. Az nyeri a labdamenetet, aki a levonás után nagyobb számot kap. Az A játékos fáradtsági szintje kezdetben 0, de ha az A játékos úgy dönt, hogy D10-et használ, annak az a hátránya, hogy a fáradtsági szintje 1-gyel növekszik, ha viszont D6-ot használ, akkor 1-gyel csökken a fáradsági szint (kipihentebb lesz), ami a következő labdamenetben már be fog számítani. Döntetlen esetén a B játékos nyer, ha az A játékos D10-el dobott, és az A játékos nyer, ha D6-ot használt.

Tegyük fel, hogy az A játékos előre eldönti, hogy melyik labdamenetben hogyan fog játszani. Kérdésünk az volt, hogy ebben az esetben hogyan érdemes játszania, hogy a legnagyobb valószínűséggel megnyerje a játékot hosszabbítás nélkül. Hosszabbítás nélkül azt jelenti, hogy négy labdamenetet nyer, és az ellenfele legfeljebb kettőt.

Labdamenetek

Nézzük meg előbb, hogy különböző fáradsági (vagy kipihentségi) értékek mellett mik a nyerési esélyek egy labdamenetre. Ha az A játékos pihen, azaz D6-al dob, akkor 6x8 = 48 kimenetel lehetséges a két játékos által dobott kockadobásokra, ha az A játékos kihajtja magát, azaz D10-el dob, akkor 10x8 = 80 kimenetel lehetséges a kockadobásokra. Ha ezeket táblázatos formában felrajzoljuk, akkor adott f fáradsági szint esetén könnyedén összeszámolhatjuk azokat az eseteket, amikor az egyik játékos nyer.

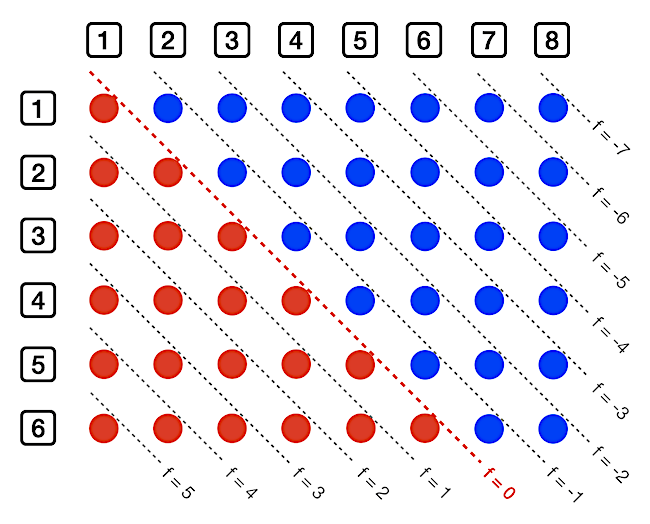
Az alábbi ábrán a pihenős (D6) labdamenethez tartozó lehetséges eseteket rajzoltuk fel. Minden pötty egy lehetséges dobáspár kimenet. A pötty sorához tartozó számérték azt határozza meg, hogy az A játékos mit dobott, lásd a sor elején lévő számot, a pötty oszlopához tartozó sorszám pedig a B játékos dobását mutatja a pöttyhöz tartozó kimenetelben. Minden fáradsági szinthez tartozik egy ferde vonal, és a ferde vonal alatti pöttyök azok az esetek, amikor az A játékos nyeri a labdamenetet. A példa kedvéért pirossal jelöltük az f = 0 fáradsági szinthez tartozó vonalat, és pirossal színeztük ezen ferde vonal alatti pöttyöket. A piros pöttyök száma ebben az esetben 21, összesen pedig 48 pötty van, tehát annak a valószínűsége, hogy laza labdamenet esetén f = 0 fáradsági szintnél az A játékos nyer 21/48, mert minden pötty (azaz dobáspár) valószínűsége azonos. Az ábráról az is leolvasható, hogy 6-os fáradsági szint esetén az A játékos soha nem fog laza játékmenetben nyerni, viszont f = -7 esetén, tehát 7-es kipihentségnél, viszont már mindig nyerne.

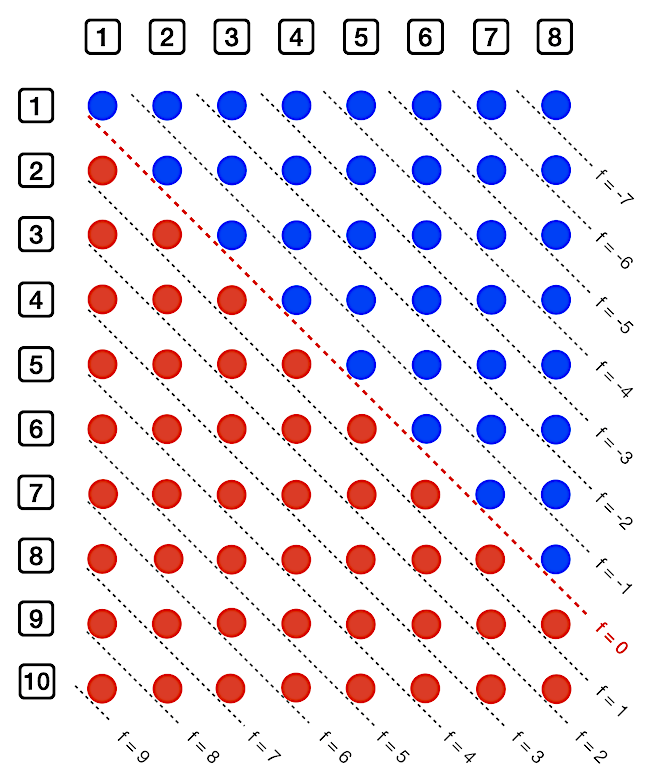
A kifáradásos labdamenet esetére, azaz D10 dobásokra, a fenti ábra úgy módosul, hogy még 4 sort a végére kell toldani, hogy összesen 10 sor legyen, továbbá a szaggatott vonalakat úgy kell berajzolni, hogy azok a pöttyöket ne felülről, hanem alulról érintsék (vagy mondhatnánk azt is, hogy f értékeit egyel balra csúsztatjuk), mert a döntetleneket most a B játékos nyeri. Az alábbi ábrán szintén pirossal illusztráltuk az f = 0 esetet, és a piros pöttyöket összeszámolva megkaphatjuk, hogy f = 0 fáradsági szint esetén az A játékos nyerési esélye 44/80.

Ezen táblázatok alapján tehát az A játékos nyerési esélyei az egyes labdamenetekre kiszámolhatók, ha rögzítjük, hogy éppen hogyan játszik és mekkora a fáradsági szintje.

A teljes játék

Az A játékos nyerési esélyét egy teljes játékra akkor tudjuk kiszámolni, ha megadjuk a stratégiáját, vagyis azt, hogy melyik labdamenetben hogyan játszik, azaz mivel dob. Egy játék legfeljebb hat labdamenetből áll hosszabbítás nélküli játékban, amire a feladat vonatkozott, ami azt jelenti, hogy az A játékos 2^6 = 64 lehetséges stratégia közül választhat, ha előre eldönti, hogyan játszik. Mindegy egyes stratégiára ki kéne számoljuk a nyerési esélyét, és megnézni, hogy ezek közül melyik a legnagyobb.

Tegyük fel, hogy választottunk egy stratégiát, hogyan tudjuk kiszámolni a nyerési esélyeket? A lehetséges végeredmények, amikben A nyer a következők lehetnek: 4 – 0, 4 – 1, 4 – 2, de az egyes eredmények többféle módon is előállhatnak, például 4 – 1, lehet úgy, hogy B az egyetlen pontját az első labdamenettel szerzi, de nyerheti a másodikat, harmadikat vagy a negyediket is, egyedül az ötödiket nem, mert akkor már az előző labdamenet után vége lett volna 4 – 0 eredménnyel. Hasonlóan 4 – 2 esetén is minden variáció lehet, csak az nem, hogy B az utolsó kettőt nyeri, mert akkor már előbb vége lenne a játéknak. Ez 4 – 2 esetén 14 féle lehetséges nyerési sorrend. Mindent összevéve tehát 1 + 4 + 14 = 19 féle képpen nyerhet A, és ezeknek a labdamenet sorozatoknak a valószínűségeit külön ki kéne számolnunk, majd összeadnunk őket.

A számolás során fontos, hogy a fáradtsági szint nem függ az eredménytől. Nézzük meg példaként azt az exrtrém stratégiát, hogy az a játékos mindig pihen. D6 használata esetén A nyerési esélyei az egyes labdamenetekben (ha az adott labdamenet sorrakerül) az alábbiak: p1 = 21/48, p2 = 27/48, p3 = 33/48, p4 = 38/48, p5 = 42/48, p6 = 45/48. Annak a valószínűsége, hogy az A játékos 4 – 0 eredménnyel nyer: p1·p2·p3·p4. Annak a valószínűsége, hogy az A játékos 4 – 1 eredménnyel nyer: (1-p1)·p2·p3·p4·p5 + p1·(1-p2)·p3·p4·p5 + p1·p2·(1-p3)·p4·p5 + p1·p2·p3·(1-p4)·p5. Annak a valószínűsége, hogy az A játékos 4 – 2 eredménnyel nyer, a 14 féle nyerési sorrendnek megfelelően egy 14 tagú összeg lesz, amiben olyan tagok szerepelnek például, hogy p1·(1-p2)·p3·(1-p4)·p5·p6, ami éppen annak felel meg, amikor a B a 2. és a 4. labdamenetet nyeri meg. Ha a 4 – 0, 4 – 1 és 4 – 2 esetek valószínűségeit összeadjuk, akkor összességében azt kapjuk (az összesen 19 tagú összegre), hogy az A játékos 78,93% valószínűséggel nyer.

A másik extrém stratégia esetében, amikor mindig D10-et használ az A játékos, akkor nyerési esélyei az egyes labdamenetekben (ha az adott labdamenet sorrakerül) az alábbiak: q1 = 44/80, q2 = 36/80, q3 = 28/80, q4 = 21/80, q5 = 15/80, q6 = 10/80. Ha erre a stratégiára is kiszámoljuk a 19 tagú összeget, akkor 7,52% nyerési esély jön ki. Láthatjuk tehát, hogy a pihenős stratégia sokkal jobb, mint a fáradásos. Sőt ha mind a 64 stratégiára kiszámoljuk az esélyeket, kiderül, hogy mind közül az a legjobb, amikor végig D6-al dob.

Érdekesség, hogy a második legjobb stratégia 78,49%-kal az, amikor majdnem végig D6-al dob, de az utolsó labdamenetben D10-el. Elsőre talán ellentmondásosnak is tűnhet a dolog, hiszen azt gondolhatnánk, hogy az utolsó labdamenetben már mindenképpen megéri D10-el dobni, hiszen a D10 választásáért járó fáradsági büntetés már nem tud érvényesülni, mert nincs következő labdamenet. Igen ám, de ne felejtsük, hogy egy labdamenet nyerési esélyeit a fáradsági szint is befolyásolja. A D10 valóban jobb a D6-nál f = 0 fáradsági szint esetén, de f = -4 fáradsági szintnél már egyformák lesznek, mert 42/48 = 70/80 = 87,5%, és ennél nagyobb kipihentségnél a D6 már jobb lesz.

Másik érdekesség, hogy bár végig D10-el játszani elég rossz, de a legrosszabb stratégai mégsem ez, hanem 5,29%-kal az, amikor az első négy labdamenetben D10-et, az utolsó két labdamenetben viszont D6-ot használunk, tehát azután próbálunk meg pihenni, hogy jól kifárasztottuk magunkat.

Kapcsolódó cikk a Qubiten: