181. feladványunkban a nagyi csokis sütijét kellett igazságosan három részre osztani. A kocka alakú réteges süti három egyforma vastagságú réteget tartalmaz, és a kocka alsó lapjának kivételével minden oldalt egyenletes csokimáz borít. Nagyi mindhárom unokája ugyanakkora részt, azaz térfogatot szeretne minden rétegből, de közben a csokimázból is egyforma mennyiséget szeretnének. A mázat a sütiről nem szabad leválasztani!

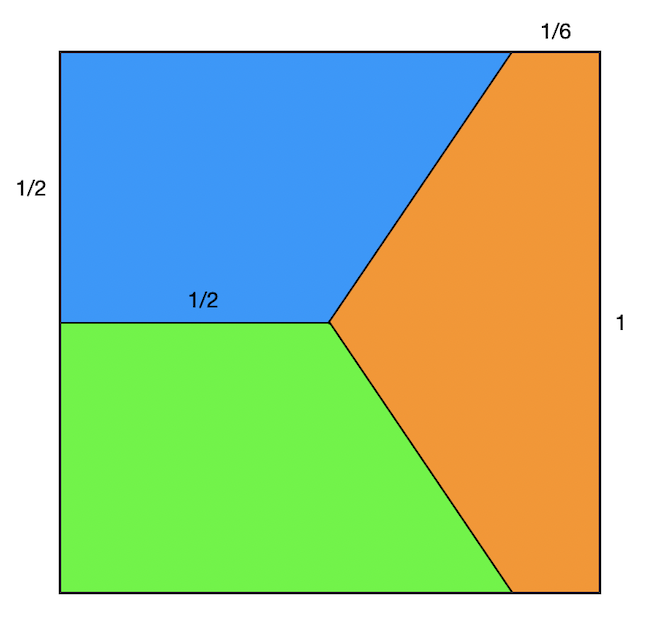
A feladatnak számos különböző megoldása lehetséges. Vegyük észre, hogy ha a süti tetejét (azaz egy négyzetet) sikerül felosztanunk három egyforma területű részre úgy, hogy azok a négyzet kerületéből is egyforma hosszúságú részeket tartalmaznak, akkor ez megoldást szolgáltat, ha a vágásokat függőlegesen lefele folytatjuk. Ez azért jó, mert a süti térfogata (minden rétegre külön-külön is) és a felső máz az egyforma területek miatt, az oldalsó mázak pedig a négyzet kerületének egyforma hosszúságú részekre darabolása miatt lesznek igazságosan elosztva. Erre egy lehetséges megoldás lehet az alábbi, ahol a három vágás pont a négyzet közepénél találkozik. A kedves olvasóra bízzuk, annak ellenőrzését, hogy a három terület valóban egyforma nagyságú, az pedig azonnal látszódik, hogy a négyzet kerületéből minden rész 1 és 2/6 részt tartalmaz, ami a teljes kerületnek, azaz 4-nek, a harmada.

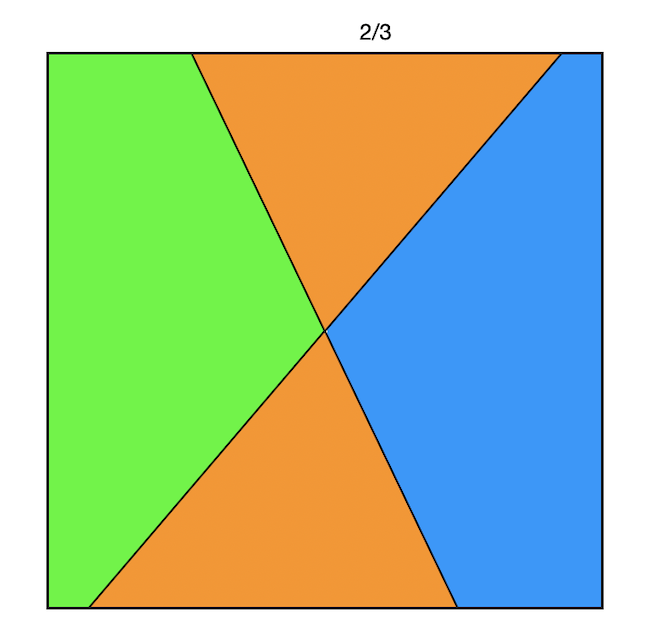
A fenti megoldás előnye, hogy mindenki egyben kapja meg a saját szeletét, viszont három vágásra van szükség. Az nyilvánvaló, hogy egy egyenes vágással a sütit csak két részre tudjuk osztani, ezért legalább két vágásra szükség van. Két egyenes vágással viszont már megoldható, ha megengedjük, hogy valaki több szeletből tegye össze a neki járó részt. Az alábbi módszert Hajós Kálmán (centrumgépész) vázolta fel nekünk. Itt két középponton átmenő egyenes vágást alkalmazunk, melyek egy forgásszimmetrikus felosztást eredményeznek. A narancs háromszög két oldala lehet eltérő ferdeségű, azaz a felosztásnak nem kell tengelyesen szimmetrikusnak lennie; a megkötés csak annyi, hogy a narancs háromszögek alapjai 2/3-ok legyenek. Ebben az esetben a két narancs rész területe 1/3 lesz, a négyzet kerületéből kimetszett rész pedig 4/3, tehát mindkettő megfelelő, és a szimmetria miatt ebből már következik, hogy mindkét maradék rész, az egymással egybevágó zöld és kék szeletek szintén megfelelőek lesznek.