Okosabb vagy, mint egy hatodikos?

Vegyük észre, hogy tetszőlegesen választott hat számjegy mindig csökkenő sorrendbe rendezhető, mégpedig egyértelműen, ezért bármely hat számjegyből pontosan egy hatjegyű lejtős szám alkotható. Egyetlen kivétel van, ha minden számjegy 0, mert 0-val nem kezdődhet szám.

Feladatunk az, hogy meghatározzuk a lehetséges tíz féle számjegy közül (0-át is beleértve) hányféleképpen tudunk kiválasztani hat számjegyet úgy, hogy egy számjegy akár többször is választható. Ha ugyanis kiválasztunk tetszőleges hat számjegyet, azokat csökkenő sorrendbe rendezve pontosan egy lejtős szám alkotható. Csak akkor nem tudunk hatjegyű lejtős számot képezni a kiválasztott hat számjegyből, ha mindegyik számjegy 0. Ha azonban csak egyetlen számjegy is van, ami nem 0, akkor már képezhető a számjegyekből hatjegyű lejtős szám, hiszen a csökkenő sorrend biztosan nem 0-val fog kezdődni.

Mármost ismétléses kombinációnak hívjuk, amikor n dologból k dolgot választunk, és minden választásnál választhatók az előzőleg választottak is. Úgy kell erre gondolni, mint egy lottósorsolásra, csak miután az urnából kihúzunk egy golyót és megnézzük, utána visszadobjuk az urnába. Jelen esetben az érdekel minket, amikor tíz golyó van az urnában, mindegyik egy számjegyet reprezentál 0-tól 9-ig, és hat golyót húzunk visszatevéssel.

A feladat átfogalmazható úgy is, hogy van tíz gyerek (0-tól 9-ig számozva) és mi hat almát szeretnénk kiosztani nekik úgy, hogy egy gyerek akár több almát is kaphat, és persze kell legyen olyan gyerek is, aki nem kap almát, hiszen több gyerek van mint alma. Ezt a feladatot megoldhatjuk úgy, hogy kilenc pálcikát helyezünk az almák közé, elé vagy mögé úgy, hogy pálcikák akár egymás után is kerülhetnek. A kilenc pálcika tíz tartományra fogja osztani az almák sorát. Az tartományokat balról jobbra megszámozzuk 9-től 0-ig. A legbaloldalibb pálcától balra lévő tartomány a 9-es, a legjobboldalibb pálcától jobbra lévő tartomány pedig a 0-ás. Egy gyerek akkor kap almát, ha az ő sorszámának megfelelő tartományba kerül alma, ha több is, akkor többet kap. Az alábbi példában a 8-as, 3-as, 2-es és 0-ás sorszámú gyerek kap egy almát, a 6-os sorszámú gyerek kap két almát, a többiek egyet se. Másrészt viszont az almáknak ezen kiosztása egyúttal egy lejtős számnak is megfelel, jelen esetben a 866320-nak, ami az almákról leolvasható.

Nyilvánvaló, hogy az almák és pálcikák minden lehetséges elrendezése megfelel pontosan egy lehetséges almakiosztásnak a gyerekek között, továbbá egy hatjegyű lejtős számnak is. Mivel viszont almákból és pálcikákból együtt 15 darab van, ezért az almák és pálcikák kiosztásának összes lehetséges száma megegyezik azzal, hogy 15 helyre hányféleképpen rakhatjuk le a hat almát, vagy 15 helyre hányféleképpen rakhatjuk le a 9 pálcikát. A két megfogalmazás teljesen ugyanaz, hiszen ha az almákat lerakjuk, akkor a pálcikák kell a maradék helyekre kerüljenek és fordítva.

A fenti pálcikás trükk segítségével tehát az ismétléses kombinációk leszámlálásának problémáját visszavezettük az ismétlés nélküli kombinációk leszámlálásának problémájára, ami viszont jól ismert és sokkal könnyebb. Általános esetben az alábbi jelölés és képlet használatos, ahol a dupla zárójel az ismétléses kombinációk számát jelöli, míg a szimpla zárójel a nem ismétléses kombinációk számát, amit úgy olvasunk, hogy (n+k-1) alatt a k.

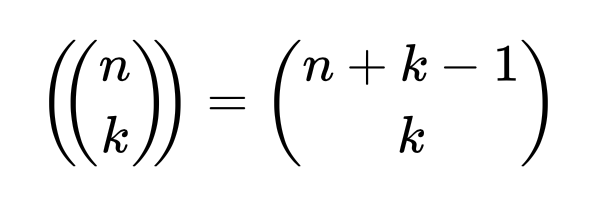
Jelen esetben n = 10, k = 6, vagyis 15 alatt a 6 értékét keressük, ami 15·14·13·12·11·10/(6·5·4·3·2·1) = 5005. Ha viszont a hatjegyű lejtős számok számára vagyunk kíváncsiak, akkor ebből le kell egyet vonnunk, ami a csupa nulla választásnak felel meg.