A rendetlenség mérése

Mi a fenének kéne megmérni a rendetlenséget? Kit érdekel, hogy mekkora valahol a kupleráj? Többeket, mint gondolnánk, a legkülönbözőbb tudósokat. Gondoljunk bele, hogy a rendetlenség a rendezettség ellentéte, vagyis ha bármiben, egy légifelvételen a növényzet mintázatában, vagy betegségek elterjedtségében, vagy akár egy ismeretlen kóddal írt szövegben valami rendszert akarunk keresni, akkor pont az érdekel minket, hogy milyen szempontból mennyire rendezett. Ennek a legegyszerűbb formája, hogy valahogy számszerűsítsük, egyáltalán van-e benne valami rendezettség, vagy ami ugyanaz, mekkora benne a rendetlenség.

A rend számszerűsítése

Te hogyan kezdenél hozzá, ha fogalmad se lenne erről a témáról? Nyilván valami nagyon egyszerű jelenségből kell kiindulni, hátha azt még valamennyire átlátjuk, értjük. Keresünk valami nagyon egyszerű rendszert, aminek kevés alkatrésze és kevésféle viselkedése van, és megnézzük, hogy mikor nevezzük rendetlennek, és mikor rendezettnek. Azt próbáljuk meg megfogalmazni, hogy mikor mondanánk rá, hogy össze-vissza működik, és mikor azt, hogy szabályosan. Én kitaláltam egy ilyen rendszert: semmi másból nem áll, mint egy teknősbékából meg egy útkereszteződésből. (A teknősbéka nagyon bonyolult állat, de most nem fogunk belenézni.) A teknőcöt lerakjuk az útkereszteződésbe, és megnézzük, hogy merre indul el. Mivel csak négyfelé tud elindulni (nevezzük ezeket Északnak, Délnek, Nyugatnak és Keletnek), a rendszer tényleg elég egyszerű. Csak azokat az eseteket nézzük, amikor a teknős nem majomkodik a kereszteződésben, hanem egyenesen elindul valamelyik úton.

Ha ezt csak egyszer csináljuk meg, akkor nem beszélhetünk arról, hogy össze-vissza működik-e a teknős, vagy szabályosan. Tehát annyival bonyolítanunk kell a dolgot, hogy kísérletek egész sorozatát végezzük el. Viszont egyszerűsítsük le a jelenséget arra, hogy nem nézzük a kísérletek sorrendjét (például lehet, hogy tavasszal másfelé hajlamos menni a teknőc, mint ősszel, vagy lehet, hogy nem szeret kétszer egymásután ugyanarra indulni, de ezekkel most ne foglalkozzunk). Tehát maradjunk abban, hogy mondjuk k-szor elvégezzük a kísérletet, és figyeljük, hogy ezek közül hányszor megy Északnak (n-szer), Délnek (s-szer), Nyugatnak (w-szer) és Keletnek (e-szer).

Százalékban kifejezve négy számról van szó: 100 × n/k, 100 × s/k, 100 × w/k és 100 × e/k. Mikor mondanánk, hogy a teknős össze-vissza működik? Nyilván akkor, ha semmi rendszert nem tudunk felfedezni a választásában. Ha például legtöbbször Észak felé indul, az már szabályosság, vagy ha Kelet felé sose megy, az is. Vagyis a legnagyobb összevisszaság az, ha kedvencünk nagyjából bármelyik irányt egyforma gyakorisággal választja.

Egy teknős, két légy, egy csapásra

Teljesen mellékes, hogy hogy hívjuk ezt, de azért jegyezzük meg, hogy ezek szerint a rendetlenség mértéke statisztikai jellegű fogalom, hiszen pont azt nevezzük statisztikának, amikor végzünk egy csomó megfigyelést vagy kísérletet, és valamilyen tömör formában megpróbáljuk összefoglalni valamilyen jellegzetességét. Igen, a teknőssel is kísérleteket végzünk, és a viselkedését tömören jellemezzük azzal, hogy mennyire kiszámíthatatlan: akkor a legszeszélyesebb, ha (jó sok kísérletet megnézve) bármelyik irányba nagyjából egyforma gyakorisággal indul el. És az is mellékes, de azért említsük meg, hogy aztán rövidebben tudjunk fogalmazni, hogy a kiszámíthatatlanságnak ezt a mértékét a tudományban entrópiának nevezik.

Tehát a teknősünk entrópiája ebben a kísérletsorozatban akkor maximális, ha mind a négy irányt nagyjából egyforma gyakorisággal választja ki. És mikor minimális? Mikor teljesen kiszámítható a teknősünk viselkedése? Hát például akkor, ha (majdnem) mindig Dél felé indul (mert mondjuk görög teknős, és haza szeretne menni). Nézzük meg ezt egy táblázaton:

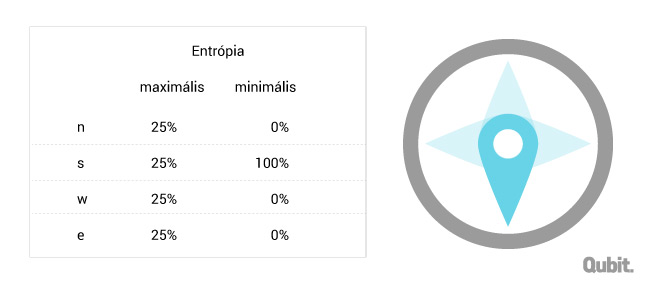
Ha tehát olyanok a kísérleti eredményeink, mint a bal oldali oszlop (jó egyenletesek), akkor maximális a rendszer entrópiája, ha meg olyanok, mint a jobb oldaliban (tehát nagyon nem kiegyenlítettek), akkor nagyon kiszámíthatóan viselkedik a rendszer, tehát minimális az entrópiája.

Nem marad más hátra, mint találni egy olyan képletet, ami az olyan kiegyenlített adatokból, mint a baloldali oszlopban szereplők, valami jó nagy számot hoz ki (nagy entrópia), az olyanokból pedig, mint a jobboldali oszlop, jó kicsi számot (akár 0-t). Előre szólok, hogy eddig a képletig ebben a rövid írásban nem fogunk eljutni, majd visszatérünk rá, amikor legközelebb találkozunk. Akkor majd szépen apránként kitaláljuk, milyen lehet a jó mérőszám, és hogy mi mindennel függ még össze a kiszámításának a módja.

Most még csak annyit, hogy kétféleképpen járhatunk el. Vagy azt mondjuk, hogy a maximális entrópia legyen mindig 1 értékű, a minimális meg legyen 0, akármilyen rendszerről van is szó. A másik lehetőség az, hogy olyan képletet keresünk, ami szerint a minimális entrópia (a teljesen megjósolható viselkedés) 0 ugyan, de a maximális entrópia rendszerenként változó: Minél bonyolultabb a rendszer, annál nagyobb. Így a maximális entrópiának nincs felső határa, mert minden rendszernél van bonyolultabb, viszont így két legyet ütünk le egy csapásra, két dolgot tudunk mérni: Az egyik légy a rendszer entrópiája, kiszámíthatatlansága, összevisszasága, a másik légy meg a rendszer bonyolultsága.

A szerző nyelvész, az MTA Nyelvtudományi Intézetének főmunkatársa

Követési, lájkolási, megosztási lehetőség: Qubit.hu a Facebookon