Megvalósulhat-e valaha a csillagközi utazás?

Rengeteg olyan sci-fit láthatunk, ahol vígan röpködnek az űrutasok a csillagok, sőt a galaxisok között is. De amikor a filmek készítői elengedik fantáziájukat, fontos dolgokat nem vesznek figyelembe. Most ne a csillagokat elválasztó fényévekre vagy milliókra gondoljunk. és ne törődjünk a jelenlegi technikai korlátokkal sem, inkább képzeljük azt, hogy a technikai fejlődés minden korlátot átléphet, csak egyet nem: a fizika törvényeit. A másik átléphetetlen korlátot élettani adottságaink jelentik. Ezeket a korlátokat számba véve vállalkozzunk gondolatban a nagy útra, hogy eljussunk a legközelebbi csillagokhoz, a Kentaur csillagkép Alfa Centauri csillagrendszerébe.
A Proxima b Földhöz hasonló tulajdonságai
Néhány éve nagy port kavart az a tudományos felfedezés, miszerint a hozzánk legközelebbi csillagrendszer egyik csillaga, a Proxima Centauri körül kering egy Föld-típusú kőzetbolygó, ami a Proxima b elnevezést kapta. Az izgalomra az adott okot, hogy ez a bolygó olyan távolságban kering a napjától, hogy az onnan érkező sugárzás valószínűleg olyan hőmérsékletet hozhat létre a bolygó felszínén, amely közel lehet a földi viszonyokhoz. Ez a távolság ugyan húszszor kisebb, mint a Föld–Nap-távolság, viszont a csillagkép napja a vörös törpék családjába tartozik, amiért az onnan érkező sugárzás intenzitása sokkal gyengébb, mint amit mi kapunk a napunktól.

Természetesen még nagyon kevés információval rendelkezünk erről a bolygóról: nem tudjuk, hogy van-e légköre, vannak-e tengerei, ami alapvető az életfeltételekhez. Ami a felszíni gravitációt illeti, az közel lehet a Földön megszokotthoz, mert a bolygó tömege 1,3-szorosa a Földének, és ha kőzetbolygóról van szó, akkor a sugara is közel lehet a miénkhez. Annyit tudunk még, hogy ott egy év nagyon rövid, mert a bolygó 11,2 nap alatt keringi körül saját csillagát, forgásáról, azaz napjai hosszáról viszont még nem tudunk semmit. Központi csillagának tömegét ki tudjuk számítani a Newton–Kepler-törvény alapján, mely szerint ez a tömeg R3/T2-el arányos, ahol az előbbi a keringési sugár, a másik a keringési idő. Számításba véve, hogy az előbbi 20-szor, az utóbbi 32,6-szor rövidebb, mint a Földé, azt kapjuk, hogy a Proxima Centauri tömege a Nap 13,3 százaléka.

Milyen sugárzás éri a Proxima b felszínét?
Az élet lehetősége szempontjából fontos a bolygóra érkező sugárzás összetétele. Vörös törpéről van szó, azaz a csillag felszíni hőmérséklete jóval alacsonyabb, mint a Napé, és a feketetest-sugárzás törvényéből tudjuk, hogy ekkor a látható, az UV- és a még nagyobb frekvenciájú sugárzás részaránya jóval kisebb a vöröshöz képest. Ez annyiban jó, hogy a csillaghoz való kis távolság ellenére az ártalmas sugárzás mennyisége kisebb lehet, de problémát jelenthet, hogy a látható tartományba kevesebb fény jut. A Föld történetéből tudjuk, hogy oxigénben gazdag légkörünket a növények, algák, egysejtűek fotoszintézisének köszönhetjük. Kérdés, hogy ha ez a sugárzási tartomány nem elég intenzív, megvalósulhatott-e a fotoszintézis a Proxima b-n, és így számíthatunk-e oxigénben dús légkörre a távoli bolygón.
Mennyi üzemanyag kell, hogy elérjük a Proxima b-t űrhajóval?
De legyünk optimisták, és induljunk ki abból, hogy megvannak az élet feltételei ezen a „második Földön”. Ekkor érdemes arra gondolni, van-e lehetőségünk, hogy eljussunk oda. A sci-fik világában ez nem okoz problémát, az űrhajók vígan röpködnek a csillagok között, csak hát ekkor nem veszik számításba, hogy mennyi és milyen üzemanyag szükséges ezekhez az űrutazásokhoz. A szükséges üzemanyag mennyiségét jelentősen csökkenthetjük, ha eleve lemondunk a visszaútról, mert ekkor nem kell magunkkal vinni üzemanyagot a visszatéréshez is. Ez messze nem felezését jelenti a szükséges üzemanyagnak, mert a megteendő út hosszával exponenciálisan növekszik ennek mennyisége. (Az exponenciális üzemanyag-szükséglet okát később fogjuk látni; a kérdéssel részletesen következő cikkünkben foglalkozunk.)
Az űrutazás élettani feltételei
A számítás kiindulópontja, hogy az élettani feltételek miatt a hosszan tartó és a földi gravitációt nagy mértékben meghaladó gyorsulás nem viselhető el. Másrészt a célba érkezéskor az űrhajót le kell lassítani, mert egyébként vagy óriási sebességgel becsapódna a bolygó felszínébe, vagy elrohanna mellette. Ezért a Földről indított rakétatechnika vagy lézersugaras indítás nem alkalmazható. Élettani szempontból az „1 g” gyorsulás az optimális, mert ekkor a földihez hasonló gravitációt érezhetünk. Lehetséges a gyorsuló szakaszok váltogatása egyenletes sebességű szakaszokkal, evvel is sok üzemanyagot takaríthatunk meg. Ebben a szakaszban az űrhajó legénysége súlytalansági állapotban utazik. Ennek időtartamát azonban korlátozni kell, mert hosszabb idő után a csontok és az izmok leépülése már komoly problémát okoz.
Váltakozó gyorsulási szakaszok az űrutazásban
Nézzünk meg egy olyan esetet, amikor az idő felét teszi ki az egyenletes sebességű, tehát súlytalansági szakasz. Itt fontos tisztázni, hogy mit értünk az utazási idő alatt, mert ez jelentősen eltér, ha a földi indulási rendszert vagy ha az űrhajóban eltöltött időt vesszük alapul, amikor a sebesség erősen megközelíti a fénysebességet, és nagy mértékben módosul a tér és idő viszonya. Példánkban a földi időből indulunk ki. A teljes t időt három szakaszra bontjuk: az első a gyorsuló t1 szakasz, a második a súlytalansági t2, a harmadik a lassulási szakasz: t3. A t1 és t3 szakasz hossza megegyezik, mert nem jelentős a Proxima Centauri sebessége a Naphoz mérten, míg legyen t2 = 2t1.
A relativisztikus sebesség változása állandó gyorsulás mellett
A nem-relativisztikus mechanikában állandó g gyorsulás esetén a sebesség arányosan növekszik az idővel: v = g·t. Ez azt jelentené, hogy egy év után már átlépnénk a c fénysebességet, ezért csak a relativisztikus effektusok figyelembevételével kaphatunk reális eredményt. Itt megkíméljük az olvasót a relativisztikus összefüggések ismertetésétől, csak annyit jegyzünk meg, hogy a fénysebesség közelében az utazási sebesség már lassabban változik, és fokozatosan közeledik c értékéhez. Az időegységet a földi évben adjuk meg, amely meglepően közel van a c = 3x108 m/s fénysebesség és a g = 9,81 m/s2 nehézségi gyorsulás hányadosához, az idődimenziójú c/g = 0,968 évhez. Ennek az aránynak különös jelentősége van további meggondolásainkban, mert megadja azt az időt, amikor már a relativisztikus hatások válnak dominánssá a klasszikus mechanikához képest.
Hogyan változik az űrhajó által megtett út a fénysebesség közelében?
A nem-relativisztikus mechanikában az állandó gyorsulás mellett megtett út s = 1/2g·t2, vagyis a megtett út az eltelt idő négyzetével arányos. Nagy sebességeknél ez az összefüggés módosul, mert azt is számításba kell venni, hogy a szóban forgó t idő alatt a fény mekkora c·t utat tesz meg. Ezt figyelembe véve egy másodfokú egyenlet írja le a megtett út és az eltelt idő kapcsolatát. Jól áttekinthető eredményre jutunk, ha az időt a már említett c/g egységben, és ennek mintájára az utat c2/g egységben adjuk meg.
A teljes utat, amit a földi koordinátarendszerben határozunk meg, három részre bontjuk: egy gyorsuló, egy egyenletes és egy lassuló szakaszra. A lassuló és gyorsuló szakasz hossza megegyezik, míg az egyenletes sebességű szakaszban a sebesség relativisztikus formuláját kell alkalmazni. Ezt az időmegosztást alkalmazva meghatározhatjuk, hogy mennyi idő alatt ér célba az űrhajó.
A Proxima Centauri Földtől mért távolsága 4,24 fényév, ami a c2/g egységekben 4,38-nak felel meg. A következő ábra mutatja az út/idő diagramot:
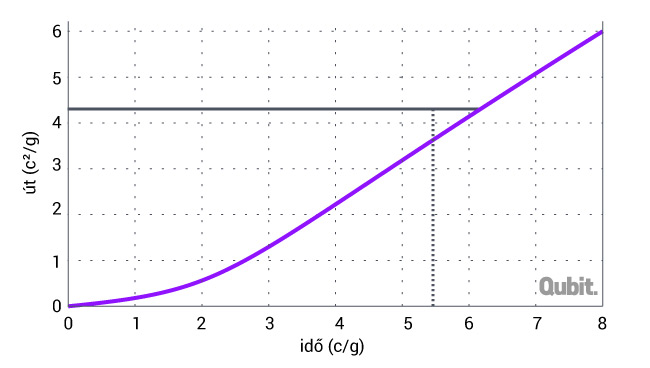
Az utazás teljes ideje földi években számolva 6,08 lesz, tehát kissé több, mint hat év. Az űrhajósok azonban ennél kevesebb időt mérnek óráikon. Ezt a különös jelenséget nevezi a fizika az idő dilatációjának. Ezt külön-külön figyelembe véve a három szakaszon azt kapjuk, hogy a gyorsuló és a lassuló szakaszok ideje 1,52 évről 1,19-ra csökken, míg az egyenletes szakaszon az idő rövidülése 3,04-ről 1,64 lesz. A a teljes út 6,08-ról 4,02 évre csökken, tehát rövidebb lesz, mint az az idő, ami alatt a fény a csillagról a Földre érkezik. Ennek oka, hogy itt különböző sebességű rendszerekben mért időket hasonlítunk össze.
Az űrhajó sebességének változása az utazás során
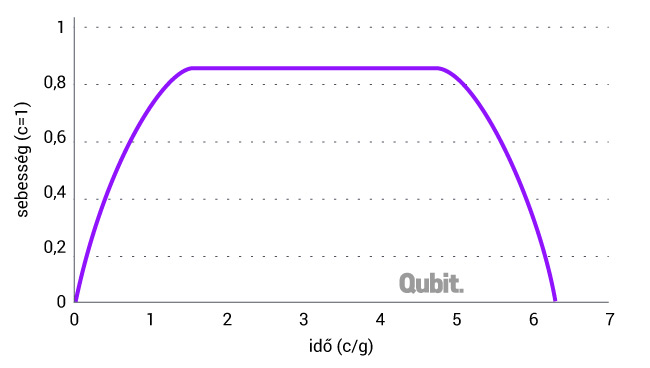
Nézzük meg, hogyan változik az űrhajó sebessége az utazás során:
Megváltozott csillagképek az űrhajóban
Az ábrából látható, hogy az űrhajó sebessége megközelíti a fénysebességet, ami jelentős mértékű relativisztikus effektushoz vezet. Nézzünk ki az űrhajó ablakából, amikor az egyenletes szakaszban vagyunk, és nagy mértékben eltérő csillagképet fogunk látni a földi megfigyelőkhöz képest. A változás nem onnan származik, hogy közben megtettünk egy-két fényévnyi utat, hiszen ez a távolság nagyon kicsi a Tejút 100 000 fényévnyi méretéhez képest – az eltérő csillagképet a nagy sebesség hozza létre.
Az űrhajó csillagászai meghatározhatják, hogy mennyire távolodtunk el Napunktól, és milyen messze van még a Proxima Centauri. Ezt összeadva megállapítják, hogy a Nap-Kentauri távolság nem 4,24 fényév, hanem csupán 2,28. Jelentősen megváltozik a Nap színe is, az otthon megszokott sárga szín helyett a vörös felé tolódik el, ugyanakkor a Proxima Centauri már nem vörös: a szín elcsúszik a kék felé. (Ezek a változások a fénytani megfelelői a hangmagasság változásának, amikor a közeledő vagy távolodó vonat füttyét halljuk magasabbnak vagy mélyebbnek.) Ha viszont nem előre vagy hátra nézünk, hanem oldalt, akkor ugyanolyan csillagkép tárul fel előttünk, amit a Földön már megszoktunk.
A megtett út a Földről és az űrhajóból nézve
Hasonlítsuk össze az út három szakaszában a megtett utat, egyrészt a földi rendszerben, másrészt az űrhajóból nézve:
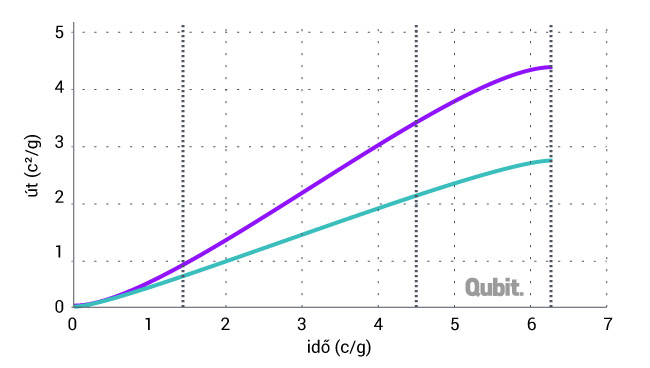
Az űrhajóban mért út lerövidül a klasszikus mechanikához képest, ezt nevezzük relativisztikus kontrakciónak. Ennek mértéke az első és harmadik szakaszban a 0,833 fényévnyi út 0,604-re, a másodikban 2,564-nek 1,377-re, a teljes 4,24 útnak 2,68 fényévre való csökkenése.
A csillagközi utazás időtávja tehát elfogadható lehet az űrhajósok számára, de még hátravan a kritikus pont: mégis mennyi üzemanyagra van szükség az utazáshoz?
A szerző a BME és az ELTE címzetes egyetemi tanára.
Mennyi üzemanyag kell a csillagközi utazáshoz?
Rockenbauer professzornak rossz híre van: nem lát reális esélyt arra, hogy eljussunk a második Földre – hacsak nem szánunk hosszú évezredeket az útra.