Elindultunk egy képzeletbeli útra az Alfa Centauri, közelebbről a második Földnek is nevezett Proxima b bolygó felé. Annak érdekében, hogy néhány év alatt odaérjünk, és a földi viszonyoknak megfelelő terhelést kapjon szervezetünk, 1 g gyorsulással indulunk, majd beiktatunk egy súlytalansági szakaszt az üzemanyag spórolás érdekében, majd a végén a lassulás szintén 1 g-vel történne. 

Itt jutunk el a kritikus kérdéshez: mégis mennyi üzemanyagra van szükség az utazáshoz? Ehhez meg kell becsülnünk a gyorsítási munkát! A problémát az jelenti, hogy a magunkkal vitt üzemanyagot is fel kell gyorsítani. Legyen ennek tömege M₀ a kilövéskor, ehhez adódik hozzá az űrhajó m hasznos tömege. A gyorsítási és lassítási szakaszban az M + m tömeg számára kell az 1 g gyorsítást biztosítani, ahol az üzemanyag mennyisége a kezdeti M₀-ról fokozatosan nulláig csökken.

Határozzuk meg, hogy mennyi üzemanyagra van szükség a gyorsítási és a lassítási szakaszban együtt! A két szakasz együttes hossza – amit számításunkban az űrhajó rendszerében kell figyelembe venni – a relativisztikus kontrakció miatt kisebb lesz, mégpedig 1,204 fényévre, azaz a c²/g egységben 1,244 hosszúságúra csökken le.  Állandó gyorsulás, illetve lassulás esetén is fokozatosan csökkenni fog a hosszegységnyi úton felhasznált üzemanyag mennyisége, mert az üzemanyag fogyása miatt egyre könnyebb lesz az űrhajó.

Mint látni fogjuk, az indulási üzemanyag mennyisége jóval meghaladja a hasznos terhet, ezért első közelítésben elegendő, ha csak ezt vesszük figyelembe. Ekkor az egységnyi út megtétele során elfogyasztott üzemanyag arányos lesz annak tömegével, amit egy k arányossági tényezővel írhatunk le. Ennek az a következménye, hogy az üzemanyag mennyisége az út során exponenciálisan csökken az említett k arányossági tényezővel: azaz M(s) = M₀·e^-k.s. A tényleges fogyás ennél gyorsabb, mert valójában az M + m teljes tömeget kell gyorsítani, ezért becslésünk alsó határt ad meg a szükséges üzemanyag mennyiségére. A lassítási szakasz végére elfogy az üzemanyag, és az űrhajó tömege egyenlő lesz az m hasznos tömeggel. A közelítés keretei között bevezethetjük m = M₀·e^-k.s egyenlőséget, amelyből becslést kapunk az üzemanyag minimális arányára a hasznos tömeghez viszonyítva:

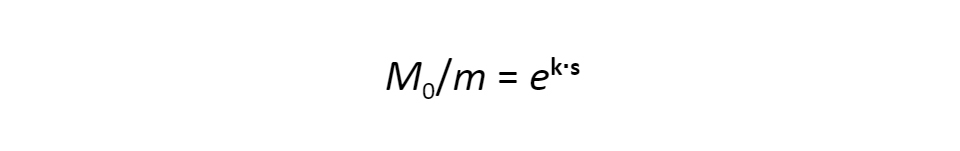
Ismételjük: az üzemanyag mennyisége ennél csak nagyobb lehet! Ez vezet el a már korábban említett,  a megtett út függvényében exponenciálisan növekvő üzemanyag-szükséglethez.

De mi határozza meg a k exponenciális állandó értékét? Itt jutunk el a relativitáselmélet legfontosabb összefüggéséhez, amely kapcsolatot teremt a tömeg és az energia között, ugyanis az M tömegű üzemanyagból nyerhető maximális energia nem haladhatja meg a nyugalmi energiát: M·c². A ténylegesen kinyert energia ennél csak kisebb lehet, amit az η hatásfoktényezővel adhatunk meg: ηM·c². Az egységnyi úthossz megtétele során felhasznált kηM·c² energia hozza létre az M·g gyorsítási munkát, amiért k = g/ηc². Ily módon kapunk alsó becslést az üzemanyag arányára a hasznos tömeghez képest:

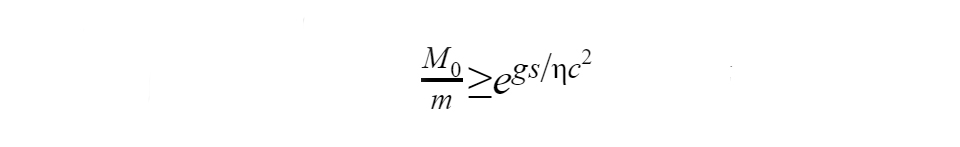
Az üzemanyag-hatékonyság szerepe az űrutazásban

Ha bármilyen kémiai üzemanyagot használunk, a hatásfok kisebb, mint egymilliárdod, nukleáris bomláskor felszabaduló energiát használva sem érhetünk el egy tízezrednél nagyobb hatásfokot (ez a felbomló radioaktív atom tömegdeficitjéből következik), még fúziós reakciókat felhasználva sem remélhetünk többet 1 százaléknál (ez a fuzionáló kis tömegű atomok tömegdeficitjéből következik). Esetünkben a relatív egységben megadott út s·g/c² = 1,244, és ezt kell osztani az alacsony η hatásfoktényezővel. Emiatt lesz rendkívül nagy az exponenciális kitevő, és még fúziós reaktor esetén is beláthatatlanul nagy mennyiségű üzemanyagra lenne szükség, akkorára, amelyhez a Tejút összes csillagának anyaga sem lenne elegendő.

A leghatékonyabb energiatermelés antirészecske-reaktorral

Tehát az expedíció alapkövetelménye, hogy az egységhez közel legyen az energiafelhasználás hatásfoka. Lehetséges-ez? Ne korlátozzuk magunkat technikai akadályokkal, és tételezzük fel, hogy az anyag-antianyag annihiláció lenne az energiaforrás: mindenekelőtt az antiproton és a protonok annihilációja lehetne az alap. A probléma természetesen az antiprotonok összegyűjtése és tárolása lenne, mert olyan tartályra lenne szükség, ahol az antirészecske nem érintkezhetne a tartály falával. Az antiproton töltött részecske, ezért mágneses térben körpályára kényszeríthető, emellett ha negatív töltésű lenne a tartály, akkor ez eltaszíthatná magától az antiprotonokat. Tehát elvben létrehozható ilyen elektromágneses csapda, de persze ehhez is energia kell, ami a működést biztosítja.

Az antirészecske-reaktor kockázatai

Az antiprotonokat a kozmikus sugárzásból lehetne nyerni, mert annak energiája elég nagy, hogy létrejöjjenek ezek a részecskék - ha viszont nagy tömegben vannak összegyűjtve, akkor a kockázat óriásira nő. Akkora mennyiség kellene belőlük, ami sokszorosan meghaladja a Földön jelenleg tárolt hidrogénbombák nukleáris töltetének teljes tömegét,  egy esetleges robbanás hatásfoka pedig ennek több mint százszorosa lenne. Elég egy apró technikai hiba, és ha létrejönne a robbanás, az nemcsak a földi életet pusztítaná el, hanem szétrobbantaná a Föld kérgét is. Még nagyobb veszély fenyegetné az űrhajósokat, mert a fénysebesség közelében már nem lehetne előre látni, ha valamilyen nagyobb űrobjektum kerülne a pálya útjába, és a manőverezés is nehéz ekkora sebességnél. Így aligha lehetne olyan biztonsági rendszert kifejleszteni, amely elegendő mértékben csökkentené az ütközés és a robbanás kockázatát.

Az elmondottak miatt bármilyen magas szintre emelkedjen a technika, a csillagközi expedíciónak rendkívül nagy lenne a kockázata. Járható út lehet azonban az automatikus űreszközök, drónok küldése, amelyeket földről irányított energiaforrások (lézerek) segítségével fel lehet annyira gyorsítani, hogy reális idő alatt elérjék a szomszédos csillagokat, és onnan küldjenek számunkra híradást a Proxima b világáról. A második Földnek elnevezett bolygóra történő utazásra viszont nem látok reális esélyt, ez megmarad mindörökre a fikciók világában – hacsak nem szánunk hosszú évezredeket az útra, és nem szoktatjuk hozzá szervezetünknek a súlytalanság körülményeihez.

A szerző a BME és az ELTE címzetes egyetemi tanára. 

Korábbi cikkünk a témában:

link Forrás