Még a lámpát sem tudnánk felgyújtani, ha nem lenne alagúteffektus

Bemutatkozik a kvantummechanikai alagúteffektus, amely ma már a mindennapi technika részévé vált az alagútdiódák kifejlesztésével, és fontos szerepe van a szerkezetvizsgálatban is a pásztázó alagútmikroszkópia területén. Sőt, ezen keresztül egy új tudományág, a kvantumbiológia kialakulásának is a tanúi lehetünk.

De mi ennek a titokzatos jelenségnek az alapja? Ennek megértéséhez szükség van a mikrovilág törvényeinek megismerésére, amelyek sokban különböznek a klasszikus mechanika megszokott szabályaitól. Induljunk ki először egy klasszikus példából: hogyan tudja egy magasugró átugrani a magasra tett lécet?

A magasugró példája

Az a sebesség, amivel egy jó ugró felpattan a rekortánról, 5 m/s körül van. Milyen magasra emelkedhet? A felfelé történő mozgás kinetikus energiája ½mv² alakul át az m·g·h potenciális energiává, amikor eléri a maximális magasságot, ezért h = ½v²/g = 127 centiméter az elérhető emelkedés. Figyelembe véve a test súlypontjának magasságát (ami az ugró testalkatától függ) ez megtoldható 80- 100 centiméterrel, de ezzel még csak maximum 227 centiméternél tartunk, aminél a magasugrás világcsúcsa jóval nagyobb (245 centiméter, Sotomayor, 1993). Ennek oka, hogy megfelelő ugrástechnikával (Fosbury flop) a súlypont alatta maradhat a léc magasságának, mert az ugrás közben a test forgást végez, és amikor a léc fölé ér, a hát meghajlításával a kéz, a fej és a lábak megfelelő pozíciójával a súlypont alacsonyabbra kerül. Természetesen az elektron nem tud hasonló eszközökkel élni, viszont segíti a kvantummechanika alagúteffektusa.

Az energiaoperátor és az állapotfüggvény

Az alagúteffektus megértéséhez elengedhetetlen a kvantummechanika néhány alapelvének megfogalmazása. Ami a legfontosabb, hogy értsük a klasszikus fizikai és a kvantumelven alapuló gondolkozás különbségét. Amikor mozgásokat írunk le, három alapkérdésre kell válaszolni: mi az, ami állandó marad, mi az, ami megváltozik, és végül mi hozza létre a változást.

Minden mozgás, minden fizikai átalakulás legfőbb állandója az energia. Ez voltaképp az energia definíciója. Ha valami időben nem változik, arra a fizika azt mondja, hogy a vizsgált rendszer állapota állandó marad. A kvantummechanika alapelve, hogy a fizikai mennyiségeket hatásuk alapján definiálja, ennek megfelelően az energiát nem egy függvénnyel, hanem a függvényeket megváltoztató operátorral írjuk le, mégpedig olyannal, amely nem változtatja meg időben a fizikai objektum állapotát. Az idő szerinti változtatás matematikai megfelelője a 𝜕/𝜕t differenciálhányados, ezt alkalmazzuk valamilyen függvényre, amit a vizsgált fizikai objektumállapot meghatározójának tekintünk. Az állapotfüggvény változatlanságán azt értjük, hogy ha képezzük ennek differenciálhányadosát, akkor egy konstans szorzótól eltekintve változatlan alakban kapjuk vissza az eredeti függvényt. Ez a konstans szorzó, amit az operátor sajátértékének nevezünk, kerül a klasszikus értelemben vett energia helyébe. Szorozzuk még meg az idő szerinti differenciálhányadost a redukált ℏ Planck állandóval és az imaginárius egységgel, hogy eljussunk az energia operátorához.

A p = m·v impulzus a mozgás másik fontos „megmaradási” mennyisége, melynek operátoros definíciója Newton első törvényéből következik, mely szerint egy test megtartja egyenes vonalú, egyenletes sebességű mozgását, ha külső erő nem hat rá, azaz az impulzus nem változik meg – a például x irányú – helyváltozás során. Ennek felel meg a 𝜕/𝜕x operátor, amelyet ℏ/i-vel szorozva kapjuk az impulzus operátorát: p = ℏ/i ·𝜕/𝜕x. Ezt behelyettesítve a kinetikus és potenciális energiából felépített klasszikus energia kifejezésébe juthatunk el a nevezetes Schrödinger-egyenlethez. (Ennek részleteit lásd: Rockenbauer Antal: A kvantummechanikán innen és túl. A fénysebességű forgás koncepciója, Scolar Kiadó, 2017.)

Az alagúteffektus potenciálfüggvénye

Az atomok világából csak akkor érkezik információ a számunkra, amikor az állapot megváltozik, és egy ugrás során fotonkibocsátás jön létre. Azokat az állapotokat, amelyek között az ugrás létrejön, nevezzük stacionárius állapotnak. A számítások alapvetően ezeket az állapotokat írják le, de amíg ezek az állapotok nem változnak meg, az időnek nincs szerepe, ilyenkor az állapot csak valószínűségi információt adhat számunkra. A mozgást leíró klasszikus fizikai pálya abban tér el a kvantummechanikai állapotfüggvénytől, hogy az előbbiben pontról pontra ismerjük a pozíciót, a sebességet és a gyorsulást, míg az elektronnál csak valószínűségi megállapításokat tehetünk.

A kvantummechanikai mozgások jellegének ismeretében lehet esélyünk rá, hogy megértsük az alagúteffektust. Kövessük a legtöbb tankönyvben ismertetett utat. Először építsük fel azt a potenciálfüggvényt, amelynek hatását le akarjuk írni. Egydimenziós közelítést alkalmazunk, amelyben az x koordináta mentén különböztetünk meg szakaszokat. Az első szakaszban azt tételezünk fel, hogy a részecske valamilyen E energiájú stacionárius állapotban van. A második szakasz x = 0-tól x = d-ig tart, ahol fellép a V₀ potenciálgát, majd a harmadik szakaszban, ahol x nagyobb d-nél, nulla lesz a potenciálgát. Stacionárius állapotról van szó, ezért mindhárom szakaszban ugyanakkora lesz az energia.

Az első szakaszban a gáthoz érkező hullám részben visszaverődik, a harmadikban pedig lesz egy továbbhaladó hullám. Számunkra az az érdekes, hogy ennek amplitúdója hogyan aránylik a bemenő hullámhoz. A kritikus a második szakasz, ahol a potenciálgát magassága meghaladja az odaérkező részecske energiáját, aminek az a következménye, hogy a gátba behatoló hullám exponenciálisan csökkenni fog, de nem szűnik meg teljesen. Annak mértéke, hogy mekkora hányada marad meg, jellemzi azt az esélyt, amivel a részecske átjut a potenciálgáton.

Az elektront az különbözteti meg a magasugrótól, hogy képes hullámként viselkedni. A számításokban szakaszonként oldjuk meg a Schrödinger-egyenletet, majd olyan feltételeket szabunk, hogy az egyes szakaszok között folytonos legyen az átmenet. A matematikai részletek dolgában ismét a fenti könyvre utalunk.

A transzmisszió függése a gátmagasságtól és szélességtől

A transzmissziós valószínűség egyaránt függ a potenciálgát magasságától és szélességétől. Ezt mutatja be az ábra az E = 1 eV = 1,6·10^-19 J energiájú elektron esetében.

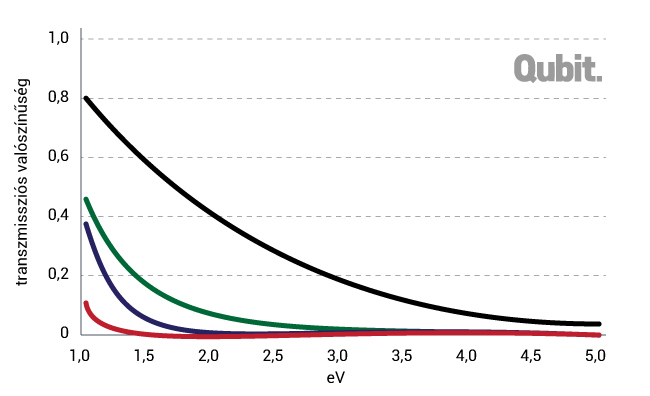
A vízszintes tengelyen a V₀ potenciálgát magassága szerepel 1 és 5 eV között, a fekete vonal felel meg 0,2 nm, a zöld 0,4 nm, a kék 0,6 nm és a piros 1 nm szélességű potenciálgátnak, demonstrálva a körülményeket, amikor a vezetőben egy, kettő, három vagy öt molekuláris szigetelő rétegen kell az elektronnak átugrani. A függőleges tengely mutatja a transzmissziós valószínűséget, ahol az egység felel meg annak az esetnek, amikor minden elektron áthalad a potenciálgáton.

Látható: ha csak egyetlen szigetelő réteg van, akkor még jelentős magasságú gáton is áthaladhat az 1 eV energiájú elektron.

Alagúteffektus az alfasugárzásban

Térjünk most vissza a magasugró példájához. A mozgás egymás utáni szakaszokra bontható térben és időben, először jön a nekifutás, majd az elrugaszkodás, és végül az ugró átlibben a léc felett. Itt az elrugaszkodás pillanatában kell összegyűjteni azt a mozgási energiát, ami elég lesz a potenciálgát leküzdéséhez. Vessük ezt össze egy kvantummechanikai példával, az alfabomlással, amit az alagúteffektussal lehet magyarázni. Ezt az atomfizika hőskorában Henry Becquerel (1896) és a Curie házaspár (Marie és Pierre) figyelte meg.

Az alfasugárzás során héliumatommagok távoznak a radioaktív elemből, míg a bétasugárzásban elektronok, a gammában nagy energiájú elektromágneses sugarak lépnek ki. A radioaktív elemet száz körüli proton és neutron építi fel. A magot összetartja a nukleonok közötti erős kölcsönhatás, amit gyengít a protonok egymást taszító hatása. A nukleonok mozgása héjakba rendeződik, a legstabilabb héjban, ezt nevezik s héjnak, két proton és két neutron helyezkedik el. A héjakban történő mozgáshoz kinetikus energia tartozik, ami azonban nem elég a magból való kilépéshez. Mégis időről időre egy-egy alfarészecske kiszabadul, ezt lehet magyarázni az alagúteffektussal.

Csillagok fúziós reakcióinak alagúteffektusa

Az alagúteffektusnak köszönhetjük, hogy a csillagok és közötte Napunk is évmilliárdokig ontják magukból a fényt és a hőenergiát. A csillagok „üzemanyaga” a két nukleon: a proton és a neutron. Ha ebből kettőt-kettőt összeházasítunk, akkor a héliummag képződésével óriásai energia szabadul fel: ez a fúziós reakció.

Van azonban egy óriási akadály: a protonok közötti elektromos taszító erő, amely olyan potenciálgátat alkot, amelyet először át kell lépni ahhoz, hogy a nukleonok elég közel kerüljenek egymáshoz, ami által a nukleáris vonzó erők működésbe léphetnek. A potenciálgát átlépéséhez még az a hőmérséklet (14 millió Kelvin) sem elég, ami a csillagok belsejében uralkodik, ezért szükség van egy közvetítő láncolatra, amelyben a héliummag több lépésben épül fel. Ennek két alaptípusát tételezik fel: míg a Napban és a hasonló méretű csillagokban a felépülés három lépcsőben történik deutériumon és ³He izotópon át, addig a nagyobb tömegű csillagokban egy hatelemű ciklus jön létre, amelyben részt vesznek a szén, a nitrogén és az oxigén izotópjai – ahol már az alagúteffektus elegendő hatásfokú az egyes reakciólépések fenntartásához. Ez jól kontrollált folyamathoz vezet, megakadályozva, hogy a csillagok szupernóvaként felrobbanjanak.

Alagúteffektus fémes, fél- és szupravezetőkben

Az alagúteffektus magyarázza, hogy miért tudjuk felgyújtani a lámpát szobánkban. A fémes vezető felülete oxidálódik, ami szigetelőréteget hoz létre a kapcsolóban. Ezt azonban az elektronok átugorhatják az ismertetett okokból.

Szupravezetőkben is fellép hasonló effektus, ami különösen jellemző a magas hőmérsékletű szupravezető kerámiákban. Ez a Josephson-effektus, amelyet felhasznál a korszerű méréstechnika is. A legismertebb alkalmazás a félvezetőket érinti: itt az alagúteffektus segítségével alakíthatunk ki olyan vezetési mechanizmust, amelyben az áram csak egy irányban folyhat, ezek az alagútdiódák. Ennek változata, amikor a dióda rezonanciaszerűen működik, mert a diszkrét kvantumnívók közötti átmenet valamilyen kritikus feszültség esetén jön létre.

A fémfelület egyes atomjainak megfigyelését teszi lehetővé a pásztázó alagútmikroszkóp (STM, scanning tunneling microscope). Működésének alapja, hogy az alagúthatás kritikusan függ két fémes vezető anyag közötti távolságtól (az egyik a mérőtű, a másik a vizsgált fémfelület). A mérés pontossága eléri a tipikus atomméret egy százalékát (0,001 nm).

Kvantumbiológia

Az alagúteffektus fontosságát felismerte a biológia is, ami egy új tudományág, a kvantumbiológia kifejlődéséhez vezetett. Ez a hatás szerepet játszik a fotoszintézisben, a sejtek lélegzésében és különböző enzimatikus folyamatokban, így a DNS spontán mutációjában is. Az utóbbi reakció a protonok alagúteffektusán alapul a hidrogénhidak átrendeződése során.

A szerző fizikus, a BME és az ELTE címzetes egyetemi tanára. A Qubiten a Kalandozások a fizikában címen futó sorozatának korábbi írásai itt olvashatók.