A dominót mindenki ismeri: két négyzet összeillesztéséből kapható elem, rajta pöttyökkel, amivel népszerű társasjáték játszható. Ha a pöttyöktől eltekintünk, és több négyzetet illesztünk össze éleik mentén, akkor kapjuk az általánosabb poliominókat. Az elnevezés Solomon W. Golomb amerikai matematikustól származik, aki 1965-ben megjelent Polyominoes című könyvében foglalkozott ilyen geometriai elemek kombinatorikájával, és vetett fel olyan problémákat is, amik máig megoldatlanok.

A téma azóta hatalmas területté nőtte ki magát, és feladványok garmadája kapcsolódik különféle poliominókhoz. Ezek közül minden bizonnyal a legismertebbek az öt négyzetből álló elemek, az úgynevezett pentominók. Ezek az elemek ugyanis még elég egyszerűek, de már elég sokfélék ahhoz, hogy rengeteg féle feladvány készíthető velük, az egészen egyszerűektől akár a több napos fejtörést igénylőkig. A legelső, még az elnevezés használata előtti pentominó-probléma 1907-ben jelent meg Henry Ernest Dudeney angol matematikus és feladványszerző tollából.

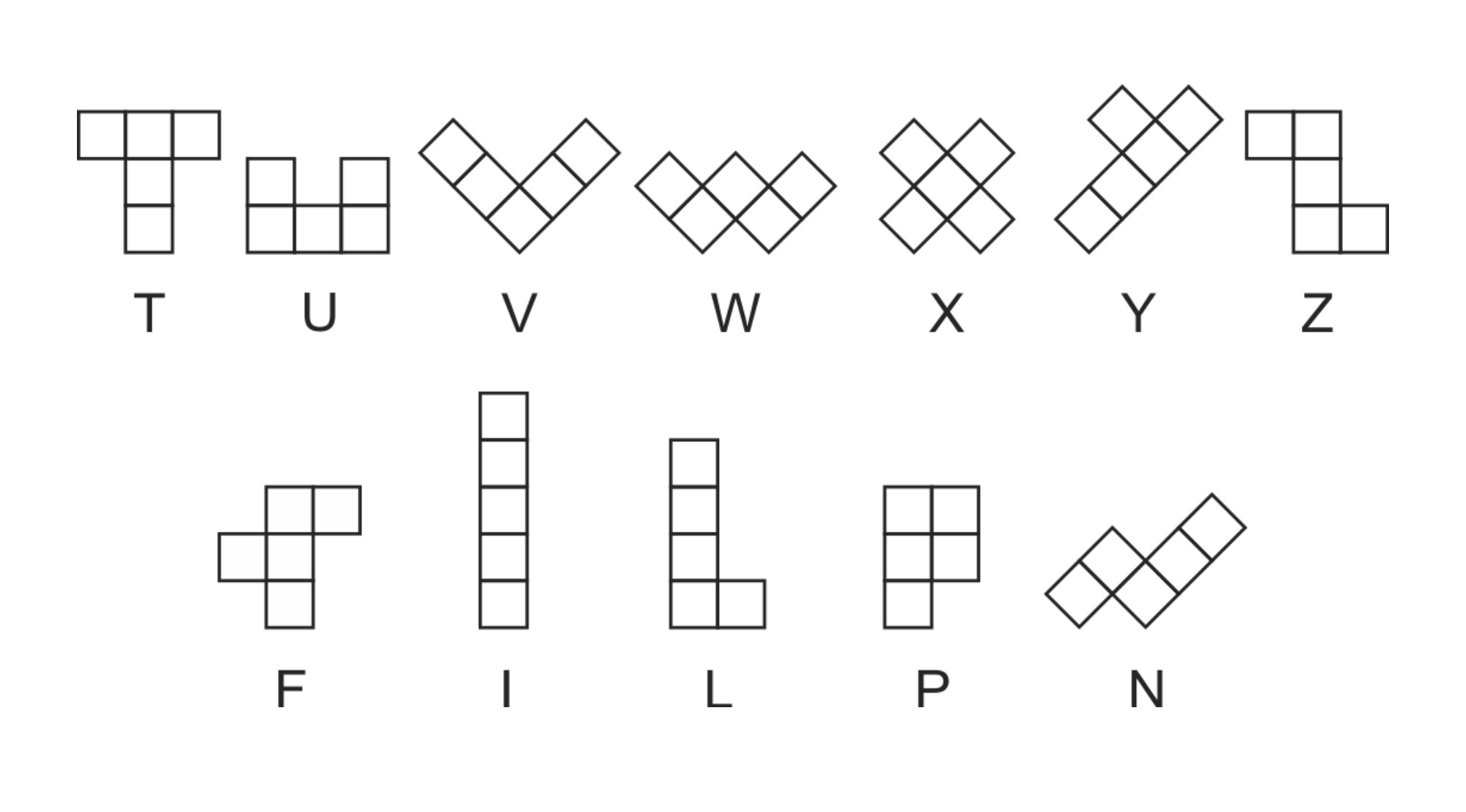
Pentominóból 18 féle van; a fenti 12, amiket az ábécé betűivel szokás jelölni, továbbá az Y, Z, F, L, P és N elemeknek a tükörképei. Mivel azonban ezekkel az elemekkel többnyire kirakós feladványokat szokás játszani, amiben az elemeket az asztalról fel lehet emelni és átfordítani, ezért ezeket nem szokás megkülönböztetni tükörképeiktől, annak ellenére, hogy a síkban mozgatva nem egymásba forgathatók.

Pentominókkal kapcsolatos fejtörő feladványok és érdekes matematikia kérdések megszámlálhatatlan mennyiségben léteznek. Magyarul a legátfogóbb írott anyag a témában minden bizonnyal Gál Péter: Ördöglakatok, pentominók és társaik című könyve, ami külön fejezetet szentel a témának. A könyvben rengeteg pentominó-feladvány található, amikből kedvcsinálónak álljon itt egy érdekes sorozat. A 12 elemű pentominókészlettel kell kirakni egy 5×13-as téglalapot, amiből az egyik pentominóelem hiányzik, lásd a jobb oldali ábrasort alább.

Ha az ember ilyen típusú kirakós feladványokat játszik, praktikusabb, ha nem négyzetrácsos papíron, ceruzával próbálkozik, hanem elkészíti az elemeket, és azokat rakosgatja. A legegyszerűbb kis kockákból összerakni az elemeket, ebben az esetben viszont már a pentominók térbeli általánosításait, az úgynevezett pentakockákat is elkészíthetjük. A pentakockák speciális esetei a kockákból összerakott pentominók, van azonban 17 pentakocka, amik nem egyrétegűek, ezek láthatók az alábbi ábrán.

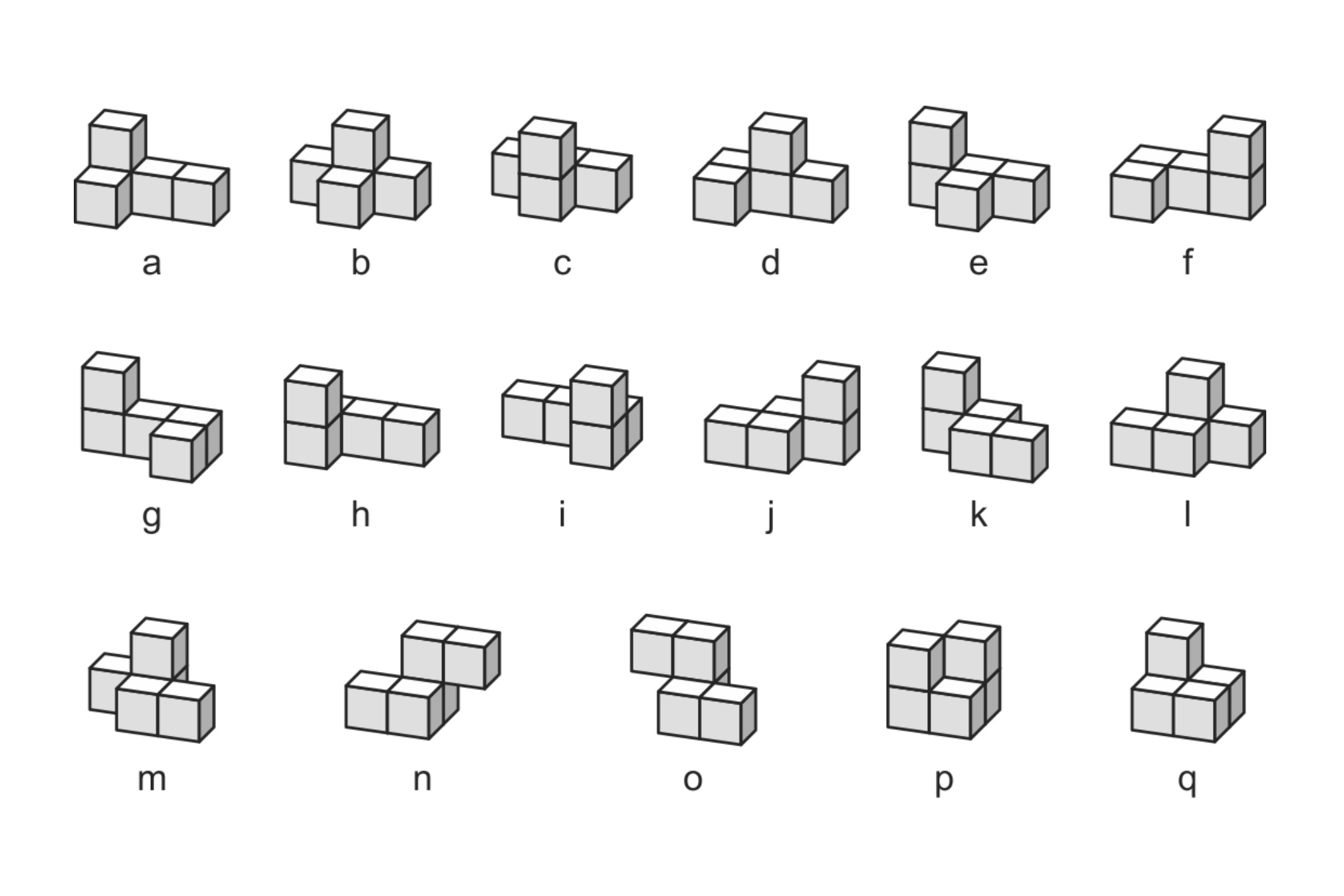
Ezek között az elemek között vannak olyanok, amik egybevágóak egymással, de nem forgathatók egymásba semmilyen térbeli forgatással. Például az n-el és o-val jelölt pentakockák egymás tükörképei. A hosszú bevezető után pedig már nem nehéz kitalálni, hogy milyen további általánosítás lesz az e heti feladvány tárgya.

49. feladvány: 4D pentakockák

Öt darab négydimenziós egységkockából hány különböző, úgynevezett négydimenziós pentakocka építhető? Az építőegységek mindegyikének érintkeznie kell másik építőkockával, mégpedig teljes oldalak mentén. Egy négydimenziós kockának nyolc oldala van, és minden oldala háromdimenziós kocka. Két négydimenziós pentakockát különbözőnek tekintünk, ha nem forgathatók egymásba semmilyen négydimenziós forgatással.

Nehézségi szint:

A megfejtéseket az eszventura@qubit.hu címre várjuk. A legértékesebb megoldást küldő versenyzők felkerülnek az Ész Ventura dicsőségfalára, közöttük és minden jó megoldást beküldő versenyző között év végén nyereményeket sorsolunk ki. Az e-mail subject mezőjében kérjük sorszámmal jelezni, hogy melyik feladvány megoldásáról van szó. Beküldési határidő: április 10. éjfél.

Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus és bűvész.