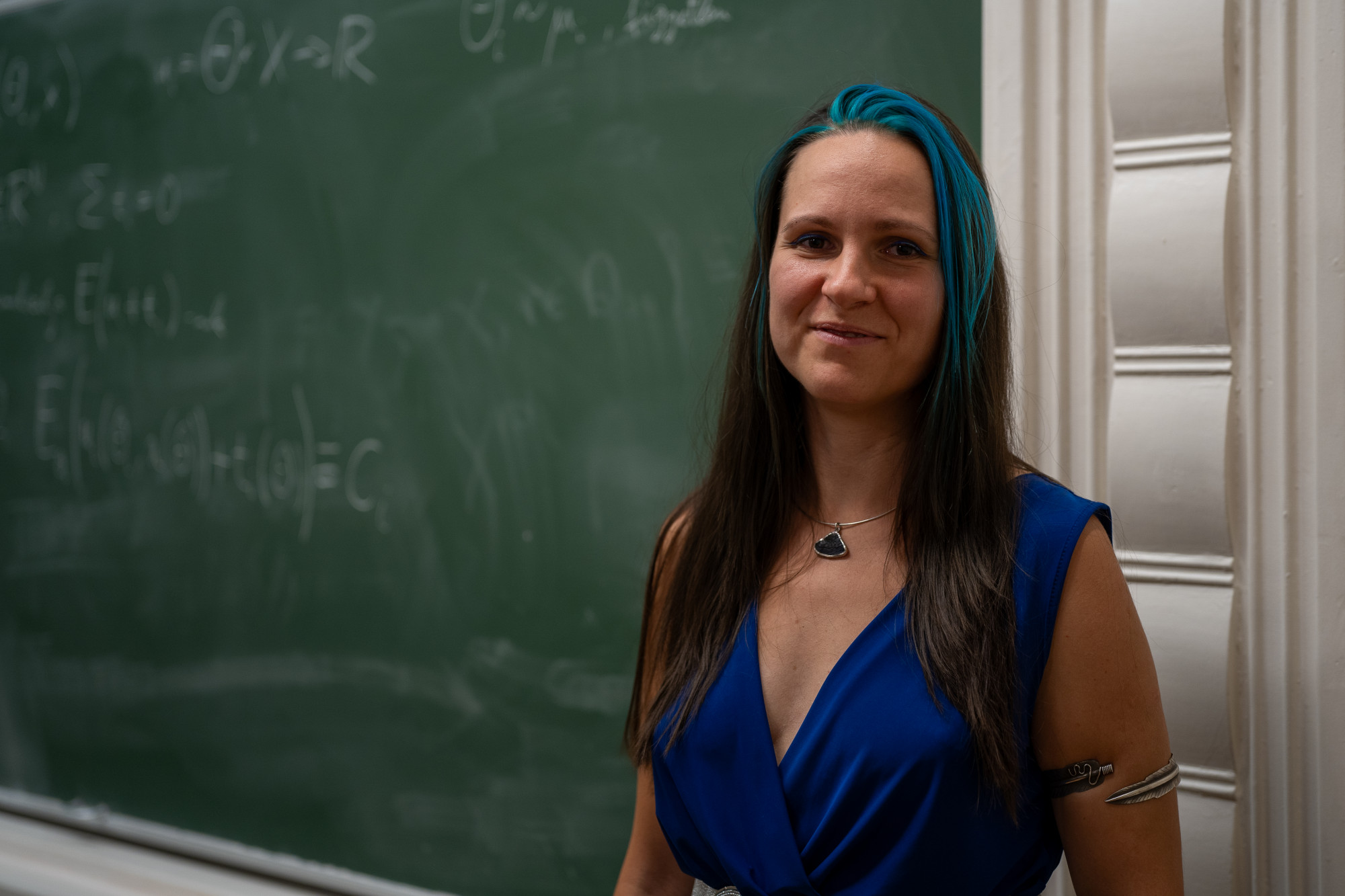
Keszthelyi Gabriella matematikus: Nagyon nagy szükség van a kritikai gondolkodásra
A kutató-oktató szerint nehéz nőként érvényesülni a matematika férfiak által uralt tudományágában. Friss könyvében kockák és érmék helyett életszerű példákkal és gyíkemberekkel igyekszik közelebb hozni a laikusokat a valószínűségszámításhoz és a statisztikához.