122. feladványunkban arra kerestük a választ, hogy az üres sakktáblán bármely három mező esetén le lehet-e rakni úgy egy vezért, hogy az támadja mind a három mezőt? A megoldáshoz Laborczi Zoltán sakkszerző ábráját és gondolatmenetét fogjuk követni. Ellenpéldát fogunk mutatni, mégpedig azt, hogy az alábbi ábrán két sötét körrel jelölt mezőhöz harmadikként hozzávéve egy tetszőleges világos körös mezőt, nem lehet úgy letenni a vezért, hogy az támadja mindhárom mezőt.

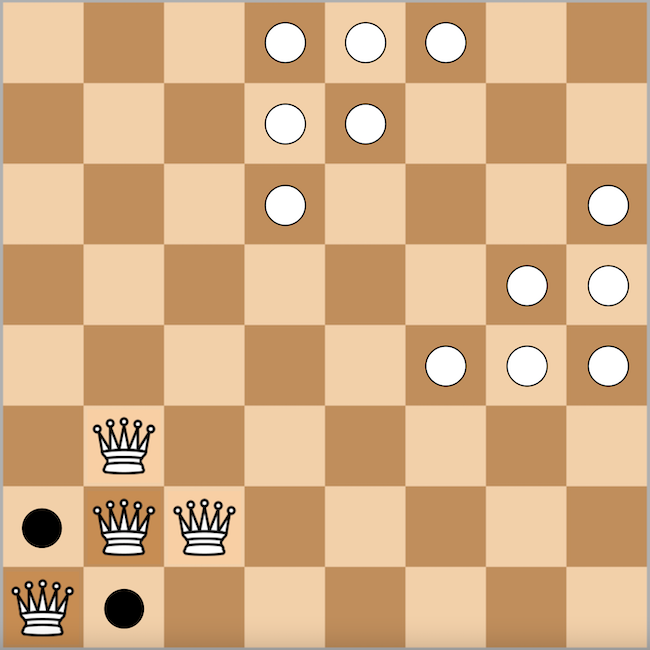
Ha a vezérnek támadnia kell a két fekete körös mezőt, az eléggé leszűkíti a lehetőségeket. A vezér lehetséges helye csak négy mezőn lehet, ezeket világos vezérrel bejelöltük a fenti ábrán. Erről a négy mezőről azonban a világos körös mezők egyikét sem ütik a vezérek, vagyis a táblán bárhova letett vezér nem támadhat egy világos körös mezőt úgy, hogy közben mindkét sötét körös mezőt is támadja. Ebből a megfontolásból az is adódik, hogy a feladvány állítása 7x7-es és 6x6-os sakktáblára sem igaz. 5x5-ös táblára viszont bármely három mező esetén elhelyezhető az őket támadó vezér, ennek belátását azonban már az olvasóra bízzuk.

A legelső megoldó és a megoldásokért kiosztott banánok megtalálhatók a Dicsőségfalon!

Kapcsolódó cikk a Qubiten: