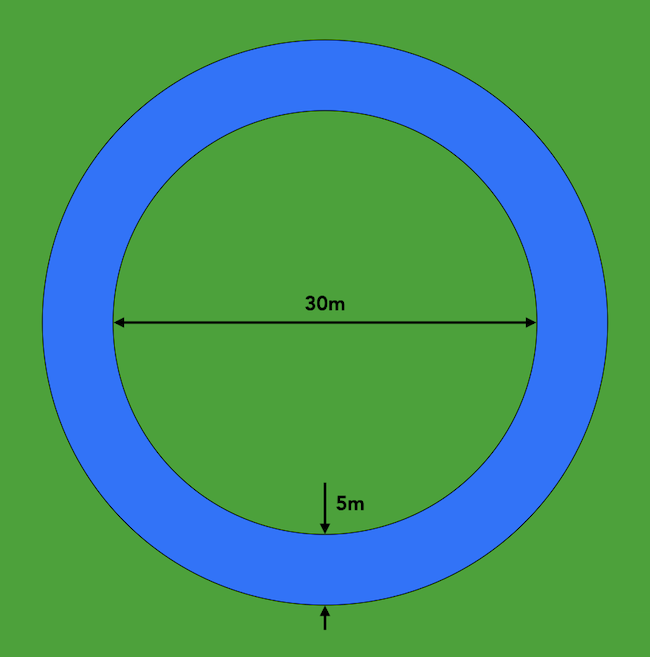
158. feladványunkban pallókból kellett hidat készíteni egy árok fölé. Az árok 5 méter széles, és egy 30 méter széles tökéletes kör alakú mezőt vesz körbe, amint az alábbi ábrán látható. A hídépítéshez semmi más nem áll rendelkezésre, csak négy darab 5 méter hosszú palló. Bár egy palló hossza pont megegyezik az árok szélességével, mégsem fektethetjük simán keresztbe az árkon, mert legalább 10 centi hosszú támasztási felülettel kell számolnunk minden támaszkodási pontnál. Egy pallót csak a part szilárd felületére vagy már korábban lefektetett pallóra támaszthatunk. A pallók szélességétől tekintsünk el a feladatban.

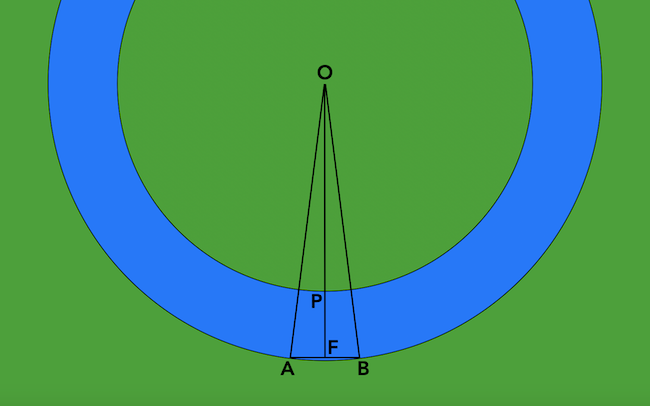
Nézzük előbb, hogy vajon két palló elég-e a hídhoz. Az egyik pallóval merev alátámasztási pontot kell biztosítanunk a másik palló számára a partvonaltól a lehető legbeljebb. A legnagyobb távolságot akkor tudjuk áthidalni, ha az első pallóval a lehető legnagyobb körszeletet vágjuk le külső körből, vagyis a lehető legnagyobb húrt alkotjuk pallóval. Mivel a palló két végén 10-10 cm alátámasztásra szükség van, ezért az ábrán AB-vel jelölt húr hossza 4,8 méter lehet maximálisan. Nézzük az OAF derékszögű háromszöget, melynek OA átfogója 20 méter hosszú, AF befogója a fentiek szerint 2,4 méter, így az OF befogó már számítható Pitagorasz tétele alapján, és kb. 19,855 méter adódik rá, tehát a PF távolság 4,855 méter, vagyis a másik pallóval nem tudjuk ezt a távolságot áthidalni.

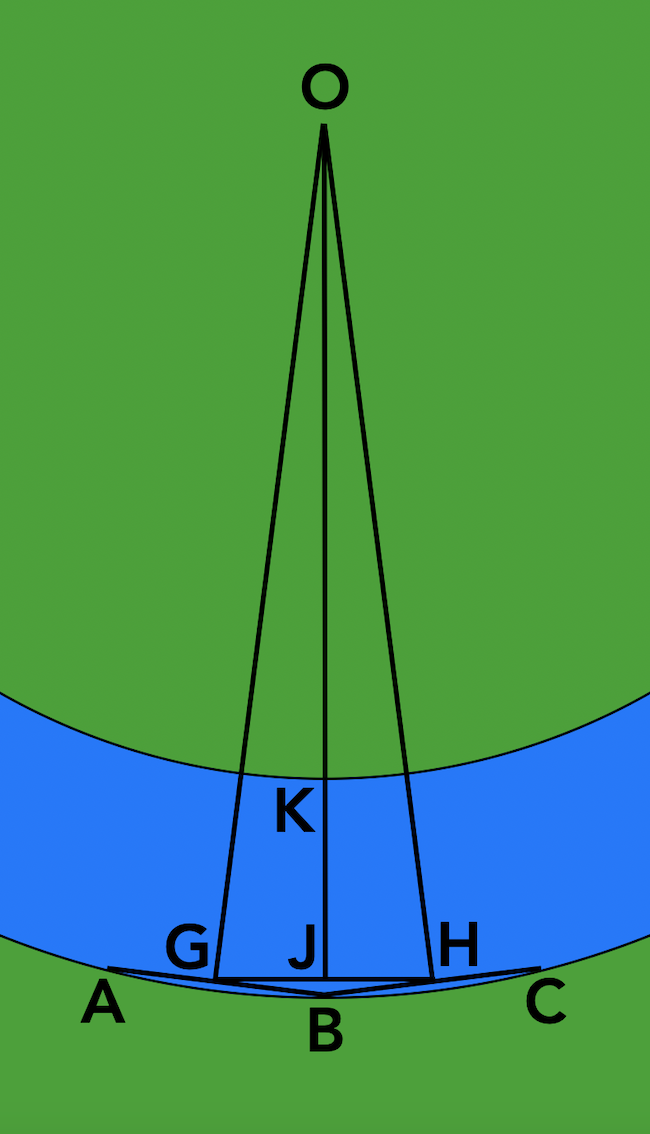
Most nézzük az alábbi tükörszimmetrikus elrendezést négy pallóval. Először két pallóval a lehető legnagyobb húrokat alkotjuk úgy, hogy legyen egy közös alátámasztási pontjuk (B). A harmadik pallót a két előzőre fektetjük szimmetrikusan és egészen addig toljuk befelé (OB-re merőlegesen tartva), hogy az GH hossza a maximális 4,8 méter legyen.

Nézzük, ha így helyezzük el az első három pallót, mekkora lesz a JK távolság, ahol J a GH felezőpontja. Ehhez jó lenne tudni, hogy mekkora az OGJ derékszögű háromszög OG átfogójának hossza, de most a G sajnos nem az AB felezőpontja, ráadásul az OGB szög sem derékszög, csak nagyon közel van hozzá. Jobban járunk ezért, ha szögekkel számoluk. Az OBA szög koszinusza 2,4/20 = 0,12, amiből az OBA szögre körülbelül 83,108° adódik, ami megegyezik a JBG szöggel. Mivel pedig BJG egy derékszögű háromszög, ezért a BGJ keskeny szög 90°-83,108° = 6,893°, mely szög tangense a JB és a GJ távolságoknak a hányadosa, tehát a JB távolság méterben kifejezve 2,4·tan(6,893°) ≈ 0,29. Tehát a KJ távolság egy pallóval áthidalható úgy, hogy 10-10 cm ráhagyással számolunk a palló két végén.

Hogy a fenti szimmetrikus elrendezéssel tudjuk-e a legnagyobb távolságot áthidalni, vagy hogy három pallóval mi lenne a legnagyobb távolság, ami áthidalható, azt a kedves olvasókra bízzuk. Aki ezekre a kérdésekre elsőként küld helyes analitikus megoldást, könyvcsomag lesz a jutalma a Typotex Kiadó jóvoltából.

Kapcsolódó cikk a Qubiten: