Elérkezett a 200. Ész Ventura feladvány. Mindenféle fejtörő volt már az elmúlt 7 évben (kategorizálva lásd őket itt), és amikor csak lehetett, igyekeztem a fejtörőket hétköznapi szituációkba helyezni, mégha ezek hipotetikusak is voltak. Természetesen a legtöbb fejtörő tartalmazott egyszerűsítéseket a frappáns megfogalmazás és a megoldhatóság végett, de néhány ilyen leegyszerűsítés éppen arra mutatott rá, hogy a hétköznapi élet (vagy épp a tudomány) valóságos gyakorlati problémái milyen összetettek tudnak lenni. Emellett a feladványok többségénél feltett bónusz kérdésekkel próbáltam arra is rámutatni, hogy a tudomány és a kíváncsi elme nem áll meg egy-egy válasznál, mert minden válasz újabb kérdéseket vet fel, ezáltal remélem sikerült az olvasókat továbbgondolásra is ösztönözni.

Ennek a hét évnek a zárásaként egy olyan szerző előtt tisztelegnék, aki a fentiekhez hasonló attitűdöt iszonyatosan komolyan vett, azt szándékosan az abszurditásig vitte, de mindezt nagyon viccesen és olvasmányosan. Az xkcd webes képregényeiről ismert Randall Munroe-ról van szó, akinek a könyveit az Athenaeum Kiadó adta ki magyarul, és ezért rendkívül hálás vagyok, mert az ismeretterjesztés egyik legjobb formája vált ezáltal magyarul is elérhetővé. Munroe azt is leköti szatirikus humorú pálcikaember-firkáival, akiket egyáltalán nem érdekel a tudomány, valami mégis ráragad mindenkire, aki olvassa új stílust teremtő könyveit, mert az abszurd kérdéseket felvető írásokból megtud valamit a világ működéséről. Eközben Munroe karikatúrái a társadalom különböző jelenségeire is reflektálnak, és sok esetben egyéb érdekes információkat is becsempész a tárgyalt kérdéskörbe. Kultikus munkássága annyira népszerű a tudományt és a humort is értékelő olvasók körében, hogy a szerzőről 2013 szeptemberében még aszteroidát is elneveztek.

Randall Munroe korábban a NASA-nál dolgozott szerződéses programozóként és robottechnikusként, de 2006-tól kezdve már teljes munkaidejét a karikatúráira és képregényeire szánta. Mi lenne ha? volt az első gyűjteményes könyve, amiben komoly tudományos megalapozottságú válaszokat adott abszurd hipotetikus kérdésekre. Ennek a könyvnek az anyagát az azonos címmel indított blogja szolgáltatta, ahol rajongói által beküldött kérdésekre adott vicces, más szempontból viszont – ahogy az már elhangzott – igen komoly tudományos megalapozottságú válaszokat. Következő könyvei is hasonló stílusban íródtak, ilyen volt a Magyarázókönyv, a Hogyan…, és idén jelent meg a Mi lenne ha? második kötete.

Könyveiben az élet minden területét érintő kérdéseket tárgyal a hétköznapiaktól a ritka szituációkig. Hogyan… című kötetéből például megtudhatjuk: hogyan fogócskázzunk, hogyan szerezzünk barátokat, hogyan adjunk medencés partit, vagy hogyan nyerjünk meg egy választást tudományos alapokon. De olyan kevésbé gyakori szituációkra is tanácsot kaphatunk, hogy miként építsünk lávaárkot vagy hogyan hajtsunk végre kényszerleszállást.

Ugyanez a könyve még a karácsonyi időszakra is tartogat érdekes olvasnivalót. A Hogyan díszítsünk karácsonyfát című fejezetből megtudhatjuk, hogy miként vágták ki világ legidősebb fáját, hogyan lehet egy fa korát kivágás nélkül meghatározni, vagy hogy a világ legidősebb fái a rókafenyők, és fura módon a sanyarú körülmények hosszabbítják meg a fa élettartamát. Ha pedig karácsonyfát keresünk magunknak, erre is kapunk tippeket: választhatunk a világ legmagasabb mammutfenyői közül, amik 110 méternél is nagyobbra nőnek, de a fejezet annak is utánajár, hogyan tudjuk a fát elszállítani és hol tudnánk felállítani, sőt arra is kapunk tippeket, hogy miként állíthatjuk ballisztikus röppályára anélkül, hogy összetörne.

200. feladvány: Fa magasságmérése

A világ legmagasabb fája egy Hyperion nevű mammutfenyő Észak-Kaliforniában, a Redwood Nemzeti Parkban. A fa magasságát több különböző módszerrel is mérték, 2006-ban például felmásztak a tetejére, és egyszerűen megmérték a lelógatott kötél hosszát. Természetesen ez sem feltétlenül tökéletes módszer, ha a kötél az ágak miatt nem tud teljesen függőlegesen haladni. Különféle geometriai számításokkal egy fa magasságát persze a földről is meg lehet mérni, ha jól látszódik a fa csúcsa, de sok esetben a lombkorona alakja olyan, hogy a csúcs a földről nem beazonosítható, vagy nem is látható. Ha a fától távolabb állva látható a csúcs, akkor egyszerű módszernek tűnhet, ha lemérjük ennek a pontnak a fától való távolságát (L), és a szöget (𝛼), amilyen szögben a csúcsot látjuk a vízszinteshez képest, és az L·tg(𝛼) képlet megadja a fa magasságát. Ezzel azonban a gyakorlatban több probléma is lehet. Az egyik az, ha a fa körül nem vízszintes a talaj, mint például a Hyperion esetében is, a másik hogy esetleg a fa nem teljesen függőleges, vagy a csúcshoz közel ferde. Illetve a mammutfenyők esetében, amelyek átmérője akár 10 méter is lehet, a fától vett távolság meghatározása sem egyszerű, hiszen a fa törzse nem pontszerű.

A példa kedvéért vegyünk most egy magas fát, aminek látszik a csúcsa, és egy füves síkságon helyezkedik el. A fa ferde, amorf és vastag törzse van, ezért a következő módszert választjuk a magasságának a meghatározásához, anélkül, hogy fel kéne mászni rá. Kijelölünk a fától távolabb három pontot a talaj síkjában, olyan módon, hogy a három pont által alkotott háromszög belsejébe essen a fa. Ezután kötelekkel lemérjük a három pont által alkotott háromszög oldalainak hosszait, majd mindhárom pontból megnézzük, hogy milyen szögben látjuk a fa csúcsát a vízszinteshez képest. Ez három hosszúságadat és három szög. Meg lehet-e ezekből határozni a fa magasságát? Ha igen, akkor mi a képlet? Ha a háromszög oldalait teljesen pontosan tudjuk mérni, de a szögeket csak bizonyos pontossággal, akkor adott szögmérési pontosság mellett hogyan érdemes megválasztani a háromszöget, hogy a magasságmérésünk pontossága a legnagyobb legyen?

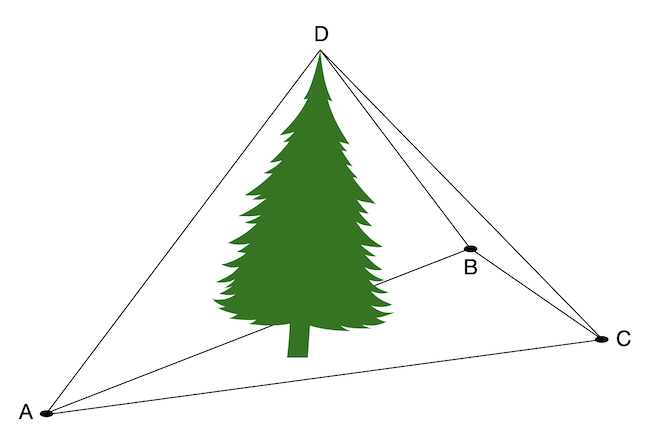
Bónusz kérdés haladóknak: Ha nem csak a fenti adatokat használjuk, hanem mérjük még a DAB, DBA, DBC, DCB, DAC és DCA szögeket is, akkor mennyivel tudjuk a magasságmérés pontosságát növelni? Mit tehetünk akkor, ha a fa nem síkságon áll, hanem egy domboldalon? Milyen mérési adatokat (földön mért hosszúságokat és különféle szögeket) kell felvennünk még, hogy meg tudjuk határozni a fa magasságát?

Nehézségi szint:

A megfejtéseket részletes magyarázattal és a szükséges ábrákkal együtt az eszventura@qubit.hu címre várjuk. A leggyorsabb és legkreatívabb megoldást küldő versenyzőink felkerülnek az Ész Ventura dicsőségfalára – közöttük és minden jó megoldást beküldő versenyző között év végén nyereményeket sorsolunk ki. A versenyről minden tudnivaló megtalálható: itt. Az e-mail subject mezőjében kérjük sorszámmal jelezni, hogy melyik feladvány megoldásáról van szó. Beküldési határidő: 2024. január 15. éjfél.

Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus, kognitív kutató, társasjáték-fejlesztő és bűvész.