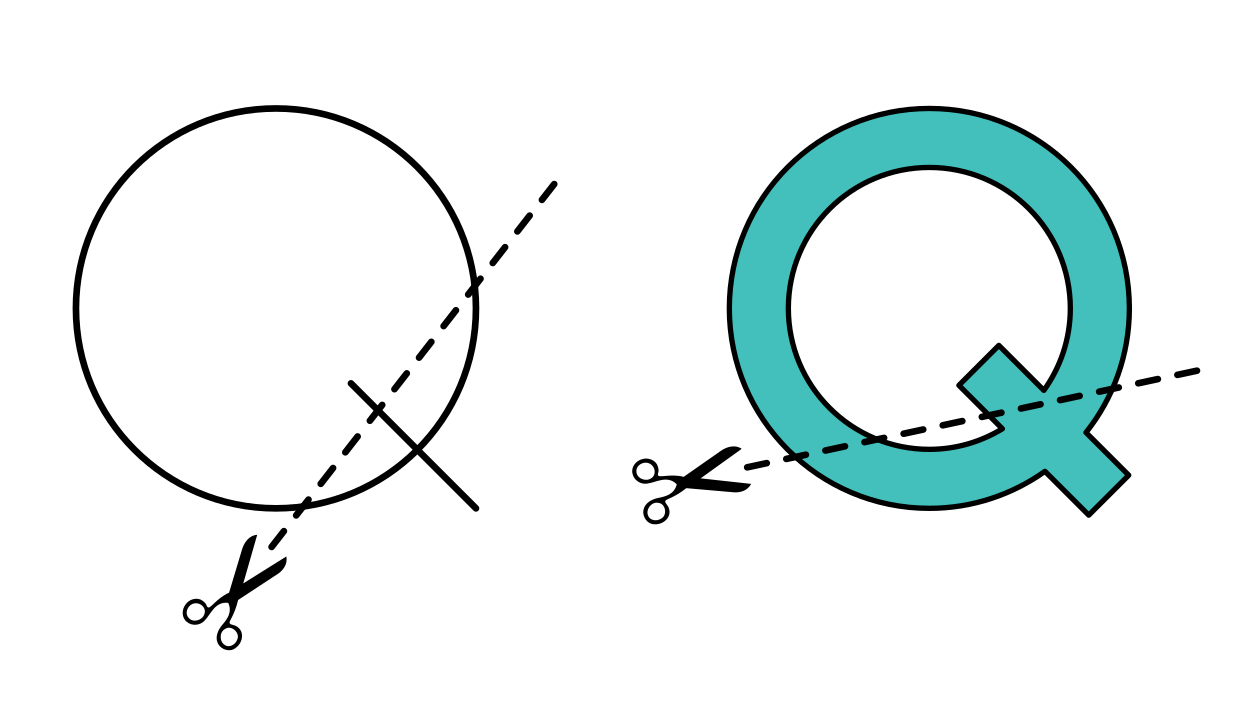
Ész Ventura: Így kellett volna felszeletelni a Q betűt

A 2. feladványnál, amelyben egy Q betűt kellett felszeletelni, próbálgatással és észszerű lépésekkel sokan eljutottak a helyes válaszhoz, azonban a legtöbben nem tudták megmutatni, hogy miért jó a válasz, sőt egyesek nem is érezték ennek szükségességét. Pedig azt, hogy a talált megoldás maximális, valamilyen módon igazolni kellene, ezt a feladat kiírásában is hangsúlyoztuk.
Ha valaki be is látja, hogy minden vágása során a lehető legtöbb új rész keletkezik, önmagában még ez sem jelenti azt, hogy a legvégén is maximális lesz a darabok száma. Mohó algoritmusnak hívják a matematikában, amikor minden lépésben az adott lépés utáni állapotra optimalizálunk, ez azonban nem jelenti azt, hogy a sok lépésre lévő végállapot tekintetében is biztosan a legjobb megoldást találjuk meg. Hozhatnánk a hétköznapi életből is példákat, amikor a pillanatnyi leghatékonyabb lépések sorozata hosszú távon nem a lehetséges legjobb végeredményre vezet. Van persze sok olyan probléma is, ahol a mohó algoritmus hatékony, és valóban a legjobb megoldást szolgáltatja, ezt azonban külön be kell látni valahogyan az adott problémára, mint ebben a feladványban is.
Fontos megjegyezni azt is, hogy a probálgatás fontos eleme lehet a megoldásnak, de a puszta próbálgatás nem vezet mindig helyes eredményre. Sokan voltak, akik beküldték próbálkozásaik végeredményét, de nem találták meg a maximális megoldást. A matematikusok is próbálgatnak, de fontos a továbblépés, hogy próbálgatásainkból levonjuk a tapasztalatokat, és megfogalmazzuk a feladat szempontjából lényeges összefüggéseket. Ha nem is bizonyítunk be matematikai precizítással minden köztes állítást, a köztes logikai lépések megfogalmazása nélkül könnyen átsiklunk a buktatókon, amik hamis eredményre vezetnek. Erre is nevel a matematikai gondolkodás, aminek a mindennapi életben is hasznát vehetjük, és nem véletlen, hogy annak idején a matekdolgozatra nulla pontot kapott az, akinek hiányzott a bizonyítás.
Vágunk-e a kereszteződésben?
Rátérve hát a konkrét megoldásokra, az első esetben, amikor a Q betű vonalát akarjuk darabolni, bármely metszéssel a kört maximum két helyen, a szakaszt pedig egy helyen metszhetjük. Egy vágással tehát maximum 4 részt kaphatunk, de ez csak akkor lehet, ha pont a kereszteződésben vágunk, hogy a szakasz körön belüli és kívüli része is különváljon a körtől. Erre sokan nem jöttek rá, és úgy vették, hogy az első vágással a Q csak három részre darabolható.
Mármost akár vágunk a kereszteződésben, akár nem, a darabok végső számát a körön és a szakaszon lévő eltérő metszéspontok száma fogja meghatározni elhelyezkedésüktől függetlenül. n darab vágással a szakaszon legfeljebb n, a körön legfeljebb 2n metszéspont keletkezhet, ami összesen 3n, kivéve ha a kereszteződésben is vágunk, mert akkor legfeljebb 3n-1.
Ha vágunk a kereszteződésben, akkor a maximális 3n-1 metszéspont 3n+1 különálló darabot eredményez, n+1 darab szakaszt és 2n darab körívet, ami n=7 esetén összesen 22 darab. És ez könnyen kivitelezhető, például az egyenes szakaszra merőleges egymással párhuzamos szelésekkel. Ha nem vágunk a kereszteződésben, akkor a maximális 3n metszéspont 3n darabot eredményez: egy kereszteződést tartalmazó darabot, 2n-1 körívet és n különálló szakaszt. Ez n=7 esetén összesen 21 darab.
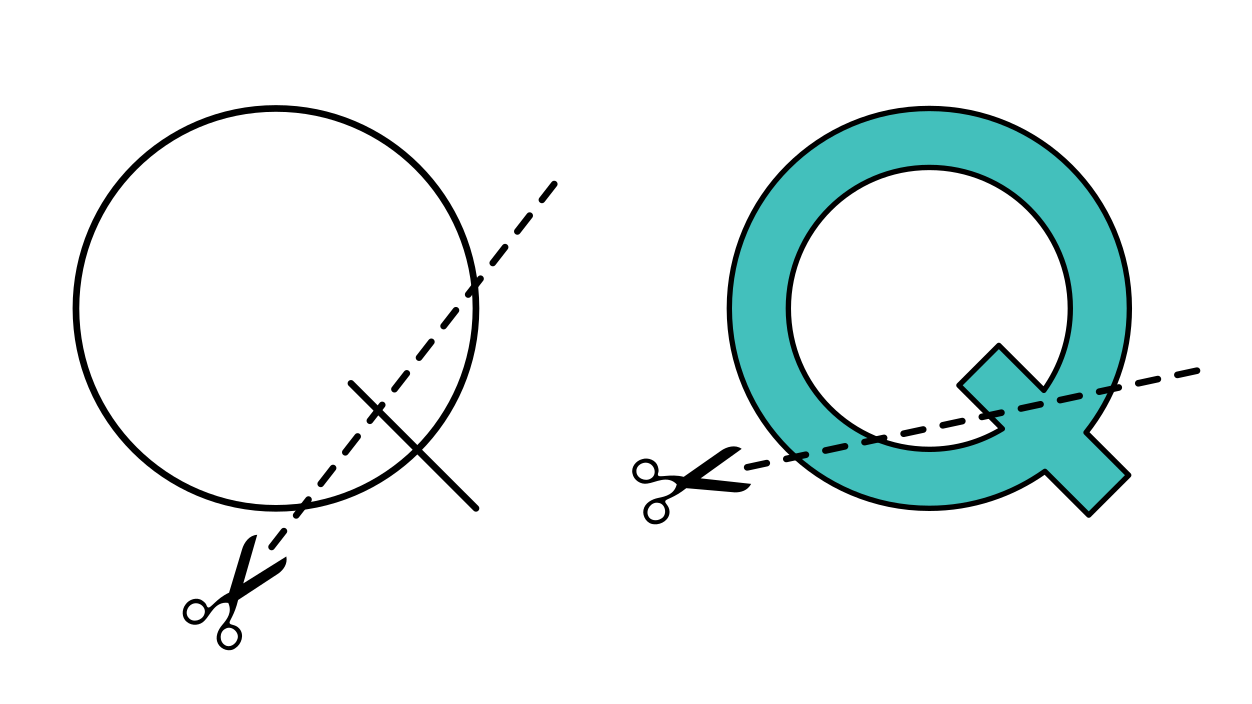
Most nézzük a haladó feladványt, amikor a Q-nak van kiterjedése, tehát egy síkidom. Könnyen belátható, hogy bármely egyenes legfeljebb 6 helyen döfheti át a határvonalát. Továbbá az első vágás legfeljebb három részre vág. Tegyük fel, hogy a Q betű már valahány részre van vágva k vágással. Függetlenül a részek számától és elhelyezkedésétől egy újabb egyenes legfeljebb 6 ponton metszheti a Q határát és legfeljebb k belső metszéspontja lehet a korábbi egyenesekkel, mindegyikkel legfeljebb 1.
Egy egyenes egy tartományt akkor tud tovább darabolni, ha valahol belemegy és valahol ki is jön belőle. Tehát legalább két metszéspont kell minden új tartományhoz az azt tartalmazó eredeti tartomány határán. A belső metszéspontokat ugyanakkor kétszer is figyelembe lehet venni, mert amint kijön az egyik tartományból az egyenes, szükségszerűen belemegy egy másikba, nem úgy, mint a Q határán lévő metszéspontok esetében, amiket csak egyszer vehetünk figyelembe.
Összességében tehát legfeljebb 2k+6 új metszéspont keletkezhet a tartományok határain, ha egy metszéspontot két tartománynál is számítunk, amennyiben mindketőnek a határán van. Ennek a 2k+6 metszéspontnak a segítségével legfeljebb feleannyi, azaz k+3 új részt keletkezhet, ha ügyesek vagyunk. Könnyen belátható ebben az esetben, hogy a mohó algoritmus adja maximális megoldást. Ha ugyanis valamelyik lépésben nem jön létre a lehető legtöbb új rész, akkor a későbbiekben már nem érhetjük el az abszolút maximumot. Ehhez persze az kell, hogy a fenti maximumot meg is lehessen valósítani. A rekurzió szerint a 7. vágásnál 3+(1+3)+(2+3)+(3+3)+(4+3)+(5+3)+(6+3) = 42 rész keletkezhet maximum. És hogy valóban keletkezhet, azt Magyar Róbert jóvoltából az alábbi ábrával szemléltetjük.
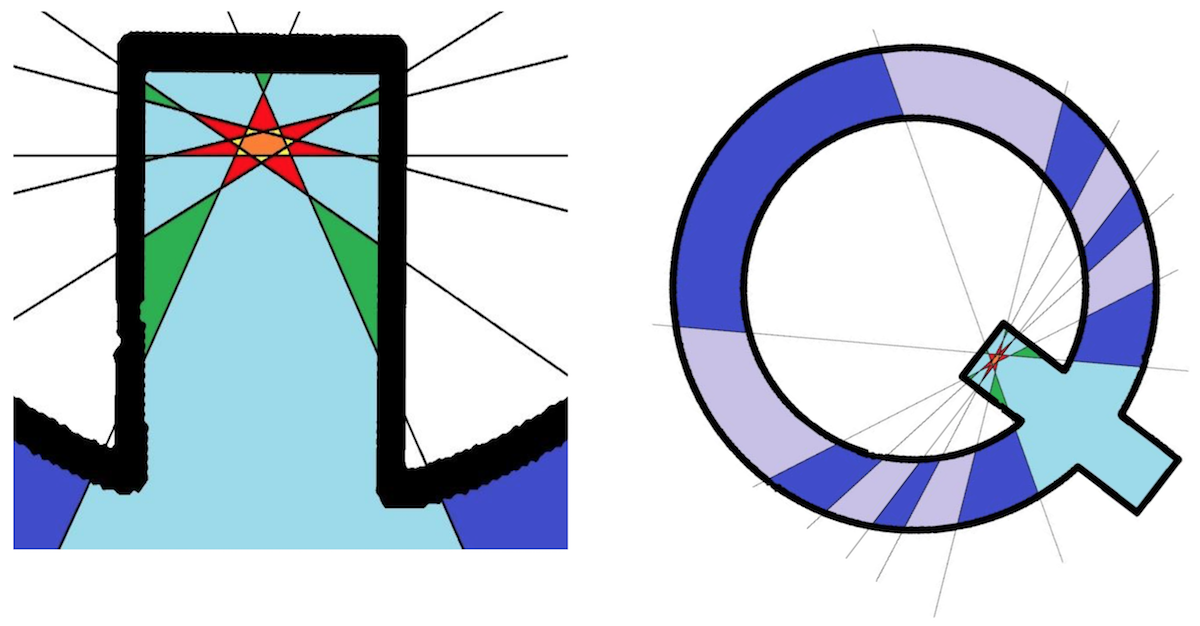
Köszönet mindenkinek a fáradozásért, reméljük hasznos volt. A legjobb megoldások beküldőit meg lehet tekinteni a frissített dicsőségfalon. Az ott szereplők között év végén ajándékokat sorsolunk ki. A részletes szabályokat a dicsőségfal alatt el lehet olvasni. További jó rejtvényfejtést a következő feladványhoz!