Az előző részben foglalkoztunk a rezgések és hullámok sajátságaival, most a rezonancia jelenségét tárgyaljuk.

Molekuláris mozgások és rezgések

Az anyagok makroszkopikus tulajdonságainak megértéséhez a molekulák energia eloszlása ad útbaigazítást. Szilárd testek belső energiáját a helyhez kötött mozgások, azaz a vibrációk határozzák meg, gázokban ehhez még hozzájárul a helyváltoztató mozgások energiája is, míg folyadékban a helyváltoztató mozgásoknak csak egyes fajtái jöhetnek létre. A lehetséges mozgástípusok összességét nevezzük a molekulamozgás szabadsági fokának. Egyensúlyi állapotban a hőmérséklet határozza meg, hogy a különböző energiaszinteken hány molekula található.

Közöljünk mechanikai energiát a rendszerrel! Ezt megtehetjük úgy is, hogy egy szilárd tárgyra kalapáccsal ráütünk, vagy egy dobra verünk rá, amely rezgésbe hozza a levegőt. Molekuláris szinten ez azt jelenti, hogy megváltozik a molekulák energiaeloszlása. A véletlenszerű mozgások kölcsönhatásba lépnek egymással (például gázokban ütköznek a molekulák), ami fokozatosan úgy változtatja meg az eloszlást, hogy az közeledni fog az egyensúlyi állapot felé. Homogén anyagokban egyetlen T időállandóval jellemezhetjük ezt a változást, amely kimondja, hogy a változás sebessége arányos az egyensúlyi eloszlástól való eltéréssel. Ennek következtében a vizsgált anyag mechanikai energiája (itt a hőenergiától eltekintünk) exponenciálisan közeledik az egyensúly felé:

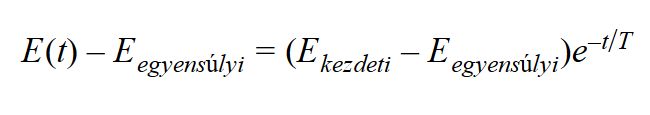
Ha egy vizsgált tárgyban rezgések, vagy egy gázban, illetve folyadékban hullámok jönnek létre, az amplitúdó csökkenni fog az említett T időállandóval. Hasonló jelenség az alapja az anyagok mágneses viselkedésének is. A mágnesezettség is csökkenni fog a gerjesztés megszűnése után, amit előzőleg periodikusan változó mágneses mező indukált. (A molekulák vagy atomok mágneses dipólus momentumainak mágneses mezőben való rendeződése mágnesezettséget hoz létre, amit a szakirodalom paramágnességnek nevez). Valamennyi felsorolt esetben a rendszer egyensúlyi állapotból való kilökése után exponenciálisan közeledik az egyensúlyhoz. Ennek oka valamilyen sebességgel arányos fékező hatás. Mozgó járműveknél ez a súrlódás, vagy közegellenállás által okozott fékezési erő, amelynek hatására, ha kikapcsoljuk a járművet meghajtó motort, a jármű fokozatosan lassul, majd megáll. Hasonló a helyzet mágneses jelenségeknél is, ahol a csillapítási mechanizmust relaxációnak nevezzük. Az energiaveszteség okozza a rezgések és hullámok x(t) amplitúdójának exponenciális csökkenését:

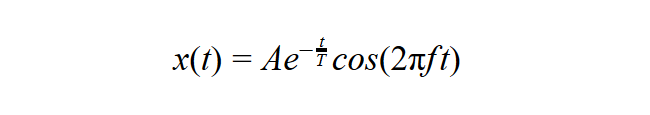
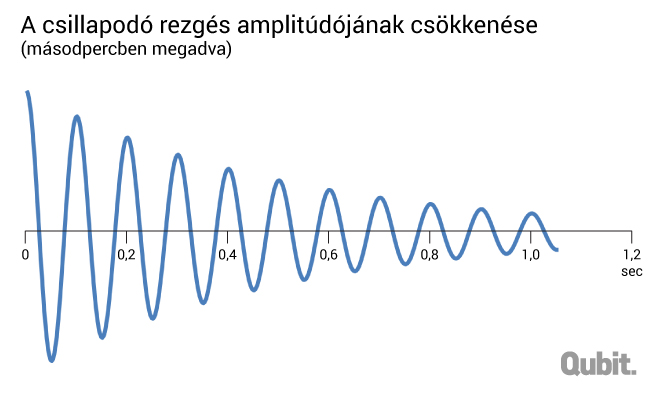
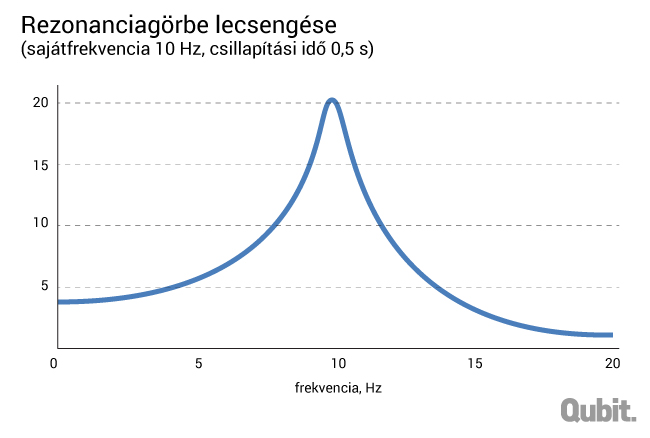
Ezt hívjuk csillapított rezgésnek, amely során a mozgási energia hőenergiává alakul át. Az f frekvencia kisebb, mint a vizsgált anyag f₀ sajátfrekvenciája, és az eltérést a csillapítás határozza meg: f² = f₀² – 1/4T². A csillapodó hullámot mutatja az ábra 10 Hz frekvenciájú rezgésnél, ahol a T csillapítási idő 0,5s.

Kényszerrezgések

Amikor periodikus erőhatást gyakorolunk egy testre, akkor rákényszeríthetjük az alkalmazott frekvenciát, ez a kényszerrezgés. Ennek is van egy átmeneti szakasza, amelynek tartamát a T csillapítási idő határozza meg, de foglalkozzunk most a periodikus válasz intenzitásával. Ennek nagysága attól függ, hogy mennyire vagyunk közel a rendszer sajátfrekvenciájához. Ha épp egyezik evvel a gerjesztő frekvencia, akkor rezonanciáról beszélünk. A periodikus gerjesztő erő időfüggése:

Az egyensúly beálltakor az f frekvenciával gerjesztett rezgés amplitúdója:

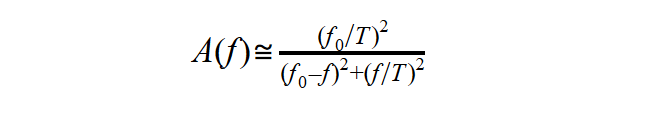
Példaként nézzük meg a rezonanciagörbét a lecsengést korábban bemutató esettel, amikor is a sajátfrekvencia 10 Hz és a csillapítási idő 0,5 s:

Mérések egyszeri és periodikus gerjesztéssel

A fizikai méréstechnikának két alaptípusa van: az egyikben meglökjük a rendszert és követjük az egyensúly időbeni visszaállását, a másikban valamilyen új egyensúlyi helyzetet hozunk létre. Legegyszerűbb példa erre a korábbi írásban tárgyalt súlymérés, ahol vagy a lengési frekvencia, vagy a megnyúlás mértéke ad felvilágosítást a súly nagyságára. A mérési pontosság szempontjából alapvető a „fékezés” hatása. Ha túl gyors a csillapodás, akkor kevesebb lengés alapján kevésbé pontos értéket kapunk a frekvenciára. Ha pedig a megnyúlást vizsgáljuk, akkor az erős csillapítás miatt a rugó nem éri el a teljes megnyúlást, mert már előbb lefékeződhet. Pontos mérés tehát gyengébb csillapítást igényel, de ekkor a hosszabb mérési idővel fizetünk a nagyobb pontosságért.

Rezonanciakatasztrófák

A rezonancia időnként katasztrófát is előidézhet. Mechanikai rezonancia okozta 1831. április 12-én a angliai Broughton híd leszakadását, mert a katonák lépéstartással meneteltek át rajta. A függőhíd 44 méter távolságú felfüggesztéséhez 88 m hullámhossz tartozik. A tranzverzális rezgés saját frekvenciája 2 Hz körül lehetett, megegyezve a menetelés ütemével, ami ezért fokozatosan megnövelte a híd kilengéseit.

Egy másik sokat emlegetett hídkatasztrófa az amerikai Tacoma Narrow Bridge esete, amelyik a szél hatására jött rezonanciába 1940. november 7-én. Itt a felfüggesztési távolság 853 méter, a torziós rezgés saját frekvenciája 0,2 Hz volt. A katasztrófa eredeti magyarázatát Kármán Tódornak köszönhetjük, akinek vortexelméletét vették alapul annak magyarázatához, hogyan alakult ki a hídon torziós oszcilláció. Később a magyarázatot pontosították nem-lineáris hatások figyelembevételével.

Mágneses rezonancia a szerkezetkutatásban

A rezonancián alapul néhány szerkezetkutatási módszer. Mágneses rezonanciát hozhatunk létre, ha az anyagokat mágneses mezőbe helyezzük, és egyúttal mikrohullámmal (ESR = Electron Spin Resonance vagy EPR = Electron Paramagnetic Resonance), vagy rádiófrekvenciával (NMR = Nuclear Magnetic Resonance) sugározzuk be. A kölcsönhatás alapja, hogy az elektronok, illetve bizonyos atommagok (például a proton) saját mágneses momentummal rendelkeznek. Mágneses mezőben a mágneses dipólusmomentumok diszkrét energiaértékeket vesznek fel, és ezek különbségét osztva a h Planck-állandóval kapjuk meg a rezonancia frekvenciát: f₀ = ΔE/h. A rezonancia akkor lép fel, amikor a sugárzási frekvencia egyezik az f₀ értékkel. A hagyományos spektroszkópiában a mágneses mező folytonos változtatásával haladnak át a rezonancián, de elsősorban az NMR-ben már rádiófrekvenciás impulzusokkal „lökik” meg a mágnesezettséget, és a lecsengő mágnesezettség jeléből egy matematikai művelettel (Fourier-transzformáció) állítják elő a 2. ábrához hasonló rezonanciagörbét. Az ESR alkalmazhatósága szempontjából tudni kell, hogy az elektron mágneses tulajdonságát elveszíti, ha a kémiai kötésben elektronpárok alakulnak ki, de előfordul bizonyos anyagokban (szabad gyökökben és egyes átmenetifém vegyületekben), amikor egyes elektronok „pár nélkül” maradnak, ekkor alkalmazható az ESR spektroszkópia. Az NMR spektroszkópia szélesebb körben alkalmazható, mert az atommagok jelentős része rendelkezik mágneses momentummal, így a proton és a ¹³C izotóp is, ami alkalmassá teszi a módszert szerves molekulák szerkezetének felderítésére. Az orvosi diagnosztika egyik fontos vizsgálati eszköze – az MRI képalkotás (Magnetic Resonance Imaging) – szintén az NMR rezonancián alapul. Hidrogén atommagok rezonanciája révén rajzolódnak ki az anatómiai részletek azokban a szervekben, melyekben magas a víz- vagy zsírtartalom.

Elektromágneses hullámok és rezonanciák

Mechanikai rezgések, hanghullámok és molekulavibrációk esetén a hullámok létrejötte a molekulák vagy atomok mozgásához van kötve. Más a helyzet az elektromágneses hullámokkal, illetve a fénnyel, amely vákuumban is terjed. Ennek példája, ahogy rádiónkkal vagy a tévével a távoli adó által kibocsátott sugárzást vesszük. Ez is rezonanciajelenségen alapul, amikor a vevő rezgőkörének frekvenciája egy adó frekvenciájára van hangolva. De mi az a „közeg” ami hordozza a rezgést, mi az ami mozog az üres térben, a vákuumban?

A klasszikus elektrodinamika válasza, hogy az elektromos és a mágneses mező rezgéseit látjuk, amely c fénysebességgel terjed. Ezt avval egészíti ki a kvantummechanika, hogy bevezeti a foton fogalmát, mint az elektromágneses sugárzás legkisebb egységét. Tekinthetjük-e az elektromos és a mágneses mezőt, vagyis a fotonokat ugyanolyan anyagnak, mint az elektront, a protont és a többi részecskét? Ha az anyag fogalmát a tömeggel azonosítjuk, akkor mondhatnánk, hogy ezek a mezők nem anyagiak, csupán matematikai leírásunk termékei, hivatkozva arra, hogy a fotonnak nincs nyugalmi tömege. De erre válaszul ott van a relativitáselmélet legfontosabb felismerése, a nevezetes E = mc² összefüggés. Minthogy a fotonnak van energiája, így van tömege is, csak ez a tömeg nem nyugalmi, hanem a fénysebességű mozgás következménye. Lásd erről részletesebben a szerző könyvében „A fény impulzusmomentuma” című pontot ( „A kvantummechanikán innen és túl. A fénysebességű forgás koncepciója”, Scolar Kiadó, Budapest, 2017, 46. oldal)

Lehet-e a tér az elektromágneses sugárzás fizikai közege?

Akárcsak a hang levegőben, a fény vákuumban egy jól meghatározott sebességgel terjed. Keressünk párhuzamot a két jelenség között! A Newton–Laplace-egyenlet szerint bármely homogén közegben a hullám terjedési sebessége 4π²c² = k’/ρ, ahol k’ a közeg rugalmasságát jellemző nyomás dimenziójú mennyiség és ρ a sűrűség. Ez vethető össze a fénysebességgel, amely kifejezhető a c² = E/m összefüggéssel a relativitáselmélet alapján. Ha egy pontból fényt bocsátunk ki, akkor az ct sugarú gömböt tölt meg a Huygens által megfogalmazott fényterjedési elmélet szerint. Osszuk el ennek térfogatával az energiát és tömeget, ekkor kapjuk az ε energia- és ρ tömegsűrűséget, evvel átírva a tömeg és energia kapcsolatát írhatjuk, hogy c² = ε/ρ. Ez már közelebb van a hanghullámok sebességképletéhez. Vegyük még figyelembe, hogy az ε energiasűrűség nyomás dimenziójú mennyiség, valamint, hogy a fénynek is van nyomása a kísérleti tapasztalatok szerint, akkor már nem tűnik indokolatlannak, ha az ε energiasűrűséget párhuzamba hozzuk a közegek rugalmasságát jellemző k’ állandóval. Az analógiából tehát az következik, hogy a tér egy fotonokkal feltöltött közeg, amely a fénynyomáson keresztül rugalmassági állandóval rendelkezik, míg a fotonok mozgási tömege képezi a közegnek tekintett tér sűrűségét.

Lehet-e dobozba zárni a fényt?

De fel lehet-e tölteni tényleg a teret fotonokkal? A válasz igen, aminek a technikai megvalósítása a mikrohullámú üreg. Képzeljünk el egy jól vezető fémekből álló üreget, például egy kockát, amelybe elektromágneses hullámokat bejuttatva a hullám az üreg falán visszaverődik. Ilyenkor állóhullámok alakulnak ki. Úgy viselkedik az üreg, mint a trombita vagy a hegedű hangdobozának belső tere, amelyben a hanghullámok ide-oda verődése állóhullámokat hoz létre. Ha az üreg mérete 3 cm, akkor ennek rezonancia frekvenciája 10¹⁰ Hz lesz. Ezt nevezik X-sávú mikrohullámú rezonátornak. Az üreg anyagától függ a jósági tényező, ami azt jellemzi, hogy hányszor verődhet egy foton a falhoz, mire elnyeli a fém. Már sikerült 10⁶ értékű jósági tényezőt is elérni, ami azt jelenti, hogy a betáplált energia 0,1 milliszekundum alatt csökken a felére. Elvben az így feltöltött üreg tömege is megnövekszik a benne tárolt energia miatt, de ennek kísérleti kimutatása már nem könnyű feladat, bár nem lehetetlen. Az elektromágneses hullámokkal feltöltött tér, tehát olyan realitás, amely alátámasztja az elképzelést, amely magát a teret tekinti az elektromágneses sugárzás fizikai közegének, és nincs szükség arra, hogy feltételezzünk bármiféle „étert”. Az éter létezését cáfolja a relativitáselmélet is.

A szerző fizikus, a BME és az ELTE címzetes egyetemi tanára.