Hullámokkal, rezgésekkel és rezonanciával gyakran találkozunk mindennapjainkban: miért szakadhat le egy híd, ha a katonaság masírozik? Mi határozza meg a hangmagasságot? Mi közvetíti a fényhullámokat vákuumban?

Az első részben a rezgésekkel foglalkozunk, közelebbről azzal, hogyan mérhetjük meg súlyunk változását, amikor az űrhajóban súlytalansági körülmények között vagyunk, és eljutunk a normál zenei A hang kérdéséig is. Nemsokára sor kerül majd a rezonanciára, hogy megértsük, miért szakadhat le a híd a masírozó katonák alatt, de arról is szó lesz, hogy mi az alapja a diagnosztikai MRI technikának, vagyis a mágnesesrezonancia-képalkotásnak.

Az olyan periodikus változások, mint a rezgések, a vibrációk vagy a hullámmozgások egyaránt megjelennek a makro- és a mikrovilágban. Megfigyelhetjük őket bármilyen fizikai közegben, legyen az szilárd, cseppfolyós vagy gáz, sőt még vákuumban is. A természetben rezeghet egy húr, rezeghet a levegő is, ami a hang formájában érkezik fülünkbe, hullámzik a víz, de rezeg az elektromágnesesség is a rádióhullámoktól kezdve a látható fényen át a gammasugarakig. Bizonyos objektumok egyes részei külön-külön is rezeghetnek, erre példa a molekulák kötéshosszának rezgése, a vibráció. De gyakran általánosítjuk a hullám fogalmat az élet, a társadalom és a gazdaság jelenségeire is. Mi a közös és mi az eltérő ezekben a periodikus jelenségekben?

A periodikus változás jellemzői

A periodikus változásoknak két típusuk van: az egyik a rezgés, amikor a periodikus mozgás helyhez kötött, a másik a hullám, amikor valamilyen közegben továbbterjed az időben ismétlődő változás. A hullámnak három fő jellemzőjét emelhetünk ki: a periodikusság hosszát egyrészt térben, másrészt időben, valamint a terjedés sebességét. A térbeli ismétlődés egysége a hullámhossz, amit a λ szimbólummal jelölünk, az ismétlődés ideje pedig a T periódus idő, amit annak reciprokával, az f=1/T frekvenciával is jellemezhetünk, végül a terjedési sebesség jele a latin celeritas szóból a c. A három mennyiség azonban nem független egymástól, mert a hullámhossz és a frekvencia szorzata a sebesség: λf = c. A hullámzás mértékének további jellemzője az A amplitúdó és a φ fázis, ami megjelenik a hullám matematikai leírásában. Ha az idő függvényében vizsgáljuk a jelenséget, akkor az Acos(2πft+φ), ha viszont az x térkoordináta mentén, akkor az Acos(2πcx/λ+φ) függvény írja le a hullámot. Gázokban és folyadékokban a rezgési amplitúdó a haladási irányba mutat, ezt nevezik longitudinális hullámnak, míg szilárd közegben a kitérés iránya a haladási irányra merőleges is lehet, ez a tranzverzális hullám. A tranzverzális hullám sebessége eltér a longitudinálistól, és általában lassabb. Erre ismert példa, ahogy földrengés esetén a longitudinális hullámok hamarabb érkeznek meg, mint a tranzverzális rezgések, az előbbiek emellett rövidebb utat járnak be, mert a Föld elasztikus magján is áthaladhatnak.

Rezgések szilárd közegben

Hogyan hozhatunk rezgésbe egy testet, és mi határozza meg a rezgés frekvenciáját? Szilárd testeknél az alaktartósság a kiindulópont, ebben különbözik a folyadékokban és gázokban létrejövő hullámoktól. Az alaktartáshoz tartozik egy erő, amely a testet eredeti alakjába hozza vissza, és ez az erő határozza meg, hogy mekkora lehet a rezgés frekvenciája. Ezt az erőt a rugalmassági modulussal jellemezzük, amely kapcsolatot teremt a test méretváltozása, például a Δl megnyúlás és az ahhoz szükséges erő között, ami egy határon belül arányos egymással: F = k Δl – ez a Hooke-törvény.

A molekulák szintén alaktartó fizikai objektumok, amelyeket az atomok közötti kötéstávolság és kötésszög jellemez. Itt az alaktartáshoz tartozó erőt a kémiai kötés erőssége határozza meg.

A rezgések és hullámok csillapodása

Van azonban egy döntő különbség a makro- és a mikrovilág objektumai között: az előbbiben a hullám vagy rezgés előbb-utóbb elhal, csillapodik, ha nem érkezik újabb lökés, míg az utóbbi „örök” rezgésre van ítélve, amit a kvantummechanika zérusponti rezgésnek nevez. Ennek oka, hogy a makroszkopikus objektumokban a periodikus mozgás rendezettsége előbb-utóbb az egyes molekulák rendezetlen mozgásába megy át különböző véletlenszerű kölcsönhatások miatt. Ezt írja le a termodinamika entrópianövekedési törvénye, amely megköveteli ezt az átalakulást. Az entrópia fogalma a nagy számok törvényéhez kapcsolódik, és ez meghatározza, hogy az egyes vibrációk hányadrésze lehet „gerjesztett”, illetve alapállapotban. Az egyedileg kiszemelt vibrációra azonban nem alkalmazható az entrópiaelv, hiszen az mindig nagyszámú részecske eloszlását írja le. Ha a vibrációs állapotok száma eltér az egyensúlyi értéktől, akkor az átmenetek száma úgy alakul, hogy a mikroállapotok által képzett makroszkopikus fizikai mennyiség (például paramágneses anyagokban a mágnesezettség, lásd később) közeledni fog az egyensúlyi értékhez. Bár minden egyes átmenet kvantált, a makroszkopikus paraméter mégis folytonosan változik, mert a molekulák óriási száma miatt az egyes ugrási lépcsőfokok a kis érték miatt nem vehetők észre.

Kvantummechanikai mozgások valószínűségi jellege

A kvantummechanika minden egyes vibrációs állapotot – az alapállapotot is beleértve – hullámfüggvény periodikus változásával írja le, de ez a mozgás közvetlenül nem „látható”, mert a stacionárius (időben nem változó energiájú) állapotok nem bocsátanak, illetve nem nyelnek el fotonokat, fotonok nélkül pedig nem kapunk információt a mikrovilágból. Információhoz úgy juthatunk, ha átmenetek jönnek létre a különböző energiájú állapotok között, például besugározzuk a kristályokat röntgensugarakkal. Ilyenkor az atomok térbeli elrendezését határozhatjuk meg, ahol az egyes atomok helyét meghatározó „foltok” nagysága tükrözi a vibrációs amplitúdót. Ez ugyan nem adja meg a vibráció időbeni lefutását, de megmutatja, hogy a rezgés során az atom mekkora gyakorisággal foglal el bizonyos pozíciókat. Ennek felel meg a klasszikus és a kvantummechanika eltérő szemléletmódja. Amíg a klasszikus mechanika az idő függvényében írja le egy fizikai objektum mozgását, addig a kvantummechanika valószínűségi eloszlásról beszél. Mindaddig, amíg a molekula vibrációja nem jár detektálható fotonok kibocsátásával vagy elnyelésével, a periodikus mozgás nem fog csillapodni. (Erről részletesebben lásd: Rockenbauer Antal, A kvantummechanikán innen és túl. A fénysebességű forgás koncepciója, IV.3 fejezetet, 65-75. oldal, Scolar Kiadó, Budapest, 2017.)

A rugó rezgései

Térjünk most vissza makroszkopikus testekhez. Rezgést szilárd testben úgy hozhatunk létre, ha energiát közlünk vele. Ez lehet egyszeri, amikor egy kalapáccsal egy fémtárgyra ütünk, vagy meghúzunk egy rugót, de lehet periodikusan ismétlődő hatás is, például amikor megfelelő ütemben hajtjuk meg a hintát, vagy húzzuk meg a harang kötelét.

Tegyünk a rugóra egy súlyt, amitől megnyúlik. A ráható erő nagyságával lesz arányos a megnyúlás, legalábbis egy határig. A megnyúlás mértéke a Δl = kmg összefüggéssel adható meg (m a tömeg, g a nehézségi gyorsulás). Ezen alapul a rugós mérleg is, amikor ismert súlyokkal kalibráljuk a mérleget, és az így meghatározott skálát használhatjuk a súly, azaz a tömeg mérésére. De mérhetünk-e tömeget az űrhajóban, ha az a súlytalanság állapotában van? Ott hiába akasztunk egy tárgyat a rugóra, az nem fog megnyúlni a gravitációs erő hiányában. Viszont meghúzhatjuk a rugót a tárggyal együtt, majd engedjük el: ekkor a rugó rezgésbe jön, aztán néhány rezgés után a mozgás megszűnik. Ez lehetőséget ad arra, hogy mérjük az időegység alatti rezgések számát, azaz a frekvenciát. A frekvencia a k erőállandó és a tömeg arányától függ. Ezt az összefüggést a Newton-féle mozgástörvényből származtathatjuk, mely szerint a gyorsulás a testre ható F erő és a tömeg arányától függ. Az egyensúlyi helyzetéből kimozdított rugót a rugalmas erő visszahúzza eredeti hosszáig, majd azon túlfut és összenyomódik. Az összenyomódott rugó azonban újra megnyúlik, és kialakul a periodikus mozgás:

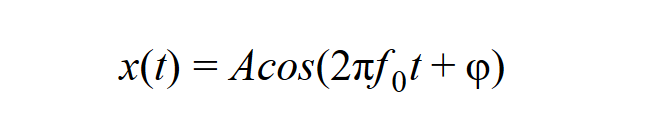
ahol f₀ a saját- vagy rezonanciafrekvencia:

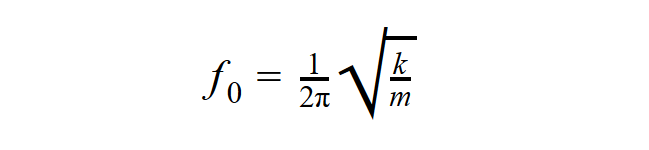
A frekvencia nem függ a kitérés A amplitúdójától, csak a k erőállandó és az m tömeg arányától. Ha a rugó saját tömege elhanyagolható a mérendő test tömegéhez képest, akkor ez az összefüggés módot ad rá, hogy az űrhajósok a súlytalanság körülményei között is meghatározzák, hogy híztak-e, vagy fogytak.

Az ingamozgás

Más példa a sajátfrekvenciára az inga vagy a hinta, de ekkor nem az anyag rugalmas ereje hozza létre a lengést, hanem a gravitációs erő. Ha az l hosszúságú matematikai inga alfa szöggel kitér a függőleges irányból, akkor a nehézségi erő érintő irányú komponense, azaz mgsinα erő fogja visszahúzni az ingát az egyensúlyi helyzet felé. Ekkor a kilengés amplitúdóját az x = αl ívhosszal jellemezhetjük. Ha nem túl nagy a kitérés szöge, sinα megegyezik a radiánban mért alfa kitérési szöggel. Ebben a közelítésben a Hooke-törvénynek megfelelő arányosságot kapunk, amelyben k = mg/l lesz. Ezt beírva a frekvencia kifejezésébe: k/m = g/l . Az összefüggés lehetőséget ad arra, hogy az inga segítségével meghatározzuk a helyi nehézségi gyorsulást a Föld különböző pontjain.

A hullámok terjedési sebessége

Mechanikai hatásokkal bármely szilárdtest rezgésbe hozható, csak az a kérdés, hogy a rezgés meddig marad fent. A közeg tulajdonságai határozzák meg a képződő hullámok terjedési sebességét, mégpedig a közeg rugalmassága és sűrűsége. Itt azért a sűrűség játszik szerepet, mert a külső deformáló erő miatt fellépő belső nyomás egyenletesen oszlik el a közegben, és ez hozza mozgásba a homogén eloszlású tömeget. Az összefüggést leíró Newton–Laplace-formulában szerepel a nyomás dimenziójú k’ rugalmassági modulus és a ρ tömegsűrűség:

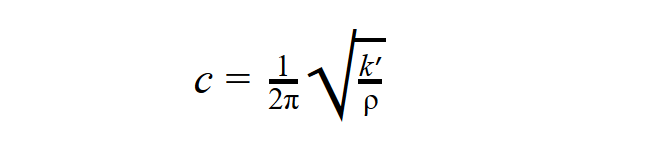
A sebesség értéke eltérő longitudinális és tranzverzális hullámoknál, mert a hullám haladására merőleges, nyírás irányú rugalmassági modulus gyengébb, mint a haladási irányú. A longitudinális sebesség vasban 5120 m/s, vízben 1484 m/s, míg levegőben jóval kisebb: 343,2 m/s, annak ellenére, hogy itt a legkisebb a közeg sűrűsége. Ennek oka a kis rugalmassági modulus, amit jóval meghalad a víz, illetve a vas nyomással szembeni kompressziós modulusa.

A zenei A hang

Folyadékokban és gázokban is érvényes a Newton-Laplace-törvény, ahol csak longitudinális hullámok jöhetnek létre. A levegőben tovaterjedő sűrűsödéseket és ritkulásokat érzékeljük fülünkkel, ahol a periodikus változás frekvenciája határozza meg a hangmagasságot. Vegyünk egy 39 cm hosszú húrt, és pengessük meg. Mit fogunk hallani? Ekkor is rezgések jönnek létre, amelyek hullámhossza a húr hosszúságához igazodik. Ha a húr két végét rögzítjük, akkor csak a húr közepe fog kitérni, amiért az alaphang hullámhossza a húr hosszának kétszerese lesz. A hullám terjedési sebességét figyelembe véve ez 6564 Hz-nek felel meg, ami rendkívül magas hang. Mi azonban csak a levegő rezgéseit hallhatjuk, mert a húron végigfutó longitudinális rezgések nem lökik meg a levegőmolekulákat, erre csak a húr irányára merőleges kitérés képes. Ez viszont a levegőben 343,2/0,78= 440 Hz frekvenciájú rezgést produkál, ami megfelel a normál A zenei hangnak. A zenészek azonban nem valamilyen húrt használnak a hangoláshoz, hanem a hangvillát, mert a húroknál kritikus a levegő hőmérséklete és a rögzítés szilárdsága, emellett zavarnak az intenzív felharmonikusok is. A hangvilla két ágának rezgési frekvenciája viszont kevéssé függ a körülményektől, és értékét a villa szárainak hosszúságán kívül annak anyaga (sűrűség és rugalmassági modulus) és keresztmetszete határozza meg.

A szerző fizikus, a BME és az ELTE címzetes egyetemi tanára.