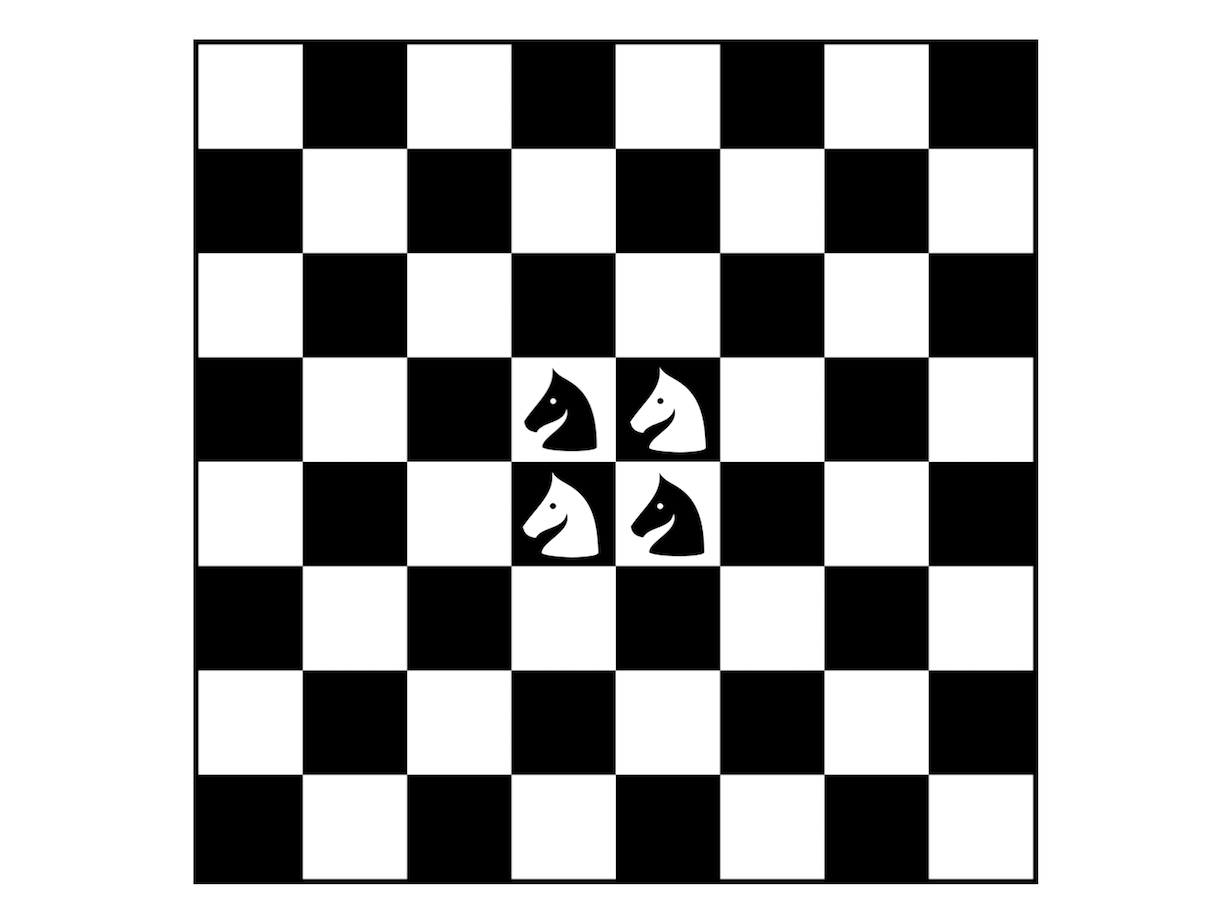
Ész Ventura: Hogyan találjunk huszárkörutakat?

A huszárkörutas feladványról sejthető volt, hogy van megoldása, sőt sok megoldása létezik. A kérdés az, hogy miként találhatunk egy konkrét megoldást. Ha csak találomra elkezdünk próbálkozni, akkor kicsi az esélye, hogy sikerrel járunk. Bár egy huszár körútjának megtalálására érdekes módon létezik jó heurisztika, ami majdnem mindig működik, az ún. Warnsdorf-szabály, de négy egymást kiegészítő huszárkörút találásához ez sajnos ilyen formában nem segít.
Egy célravezető stratégia az, ha lecsökkentjük a kombinációs lehetőségeket, azaz extra feltételeket kötünk ki, lényegében saját magunkat korlátozva. Ha olyan mértékben korlátozzuk magunkat, hogy még mindig legyen sok megoldás, amikből van esélyünk rátalálni egyre, ugyanakkor ezen korlátok között a próbálgatás és ellenőrzés átláthatóbb és gyorsabb, akkor az nagy segítség.
Legtöbben a forgásszimmetriát kötötték ki extra feltételnek, azaz olyan megoldást kerestek, amiben a négy ló lényegében ugyanazt az utat járja be, csak elforgatva 90, 180 és 270 fokkal. Ilyen megoldásból 560 létezik, két beküldőnk program segítségével meg is találta az összes ilyent, lásd az animált gifet alább Boros Péter megoldónk jóvoltából. Bár ezeknek csak a fele lényegileg különböző, hiszen ugyanaz az út visszafele bejárva is megoldás. Viszont egyáltalán nem volt szükséges programozni, mert a forgásszimmetria kikötése elég sokat segített ahhoz, hogy puszta próbálgatással is lehessen forgásszimmetrikus megoldást találni.
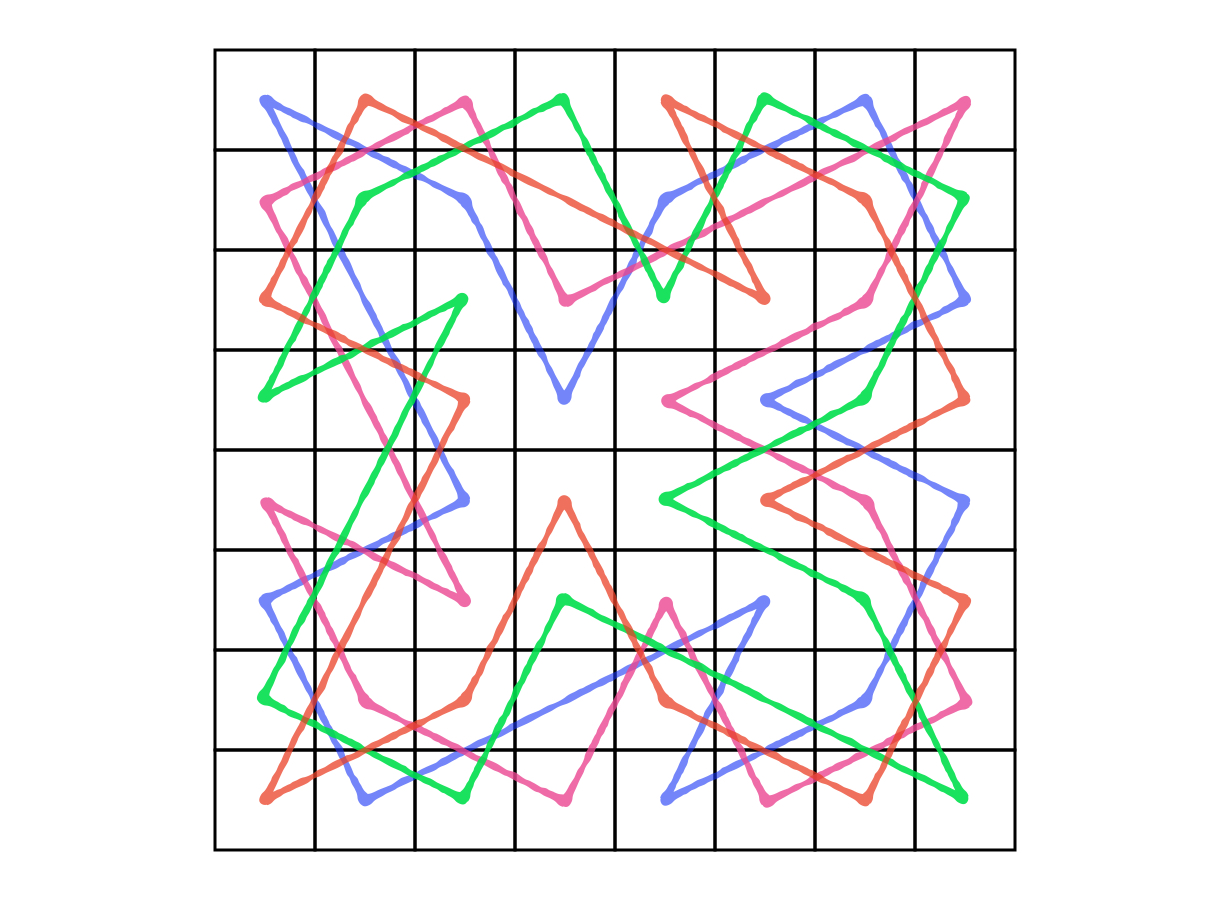
Vannak azonban még ennél is szimmetrikusabb és strukturáltabb megoldások. Kettőt említenék meg, melyek egyike sincs a fenti 560 forgatásos megoldások között. Az alábbi megoldásban két huszár a tábla egyik felét járja be, a másik két huszár pedig a másik térfelet. Itt az utak nem forgatással, hanem tükrözéssel kaphatók meg egymásból. Mivel pedig a huszárok kezdő állás szerinti pozíciói (üres körök) eltérő utakhoz tartoznak, a feladat szövege akár úgy is hangozhatott volna, hogy be tudják-e járni a huszárok a saját térfelüket a kezdőpozíciókból úgy, hogy ugyanoda visszaérkezzenek, és közben minden mezőt pontosan egyikük érint.

A másik megoldás egy olyan konstrukció, amiben szinte semmi próbálgatás nincsen. Bontsuk fel a sakktáblát négy darab 4×4-es blokkra, és vegyük észre, hogy minden ilyen blokk lefedhető négy darab 4 hosszú kis körúttal, amik összességében lefedik az egész sakktáblát. Már csak össze kéne nyitni bizonyos helyeken ezeket a kis körutakat, hogy megfelelő méretű nagy körutakat kapjunk.
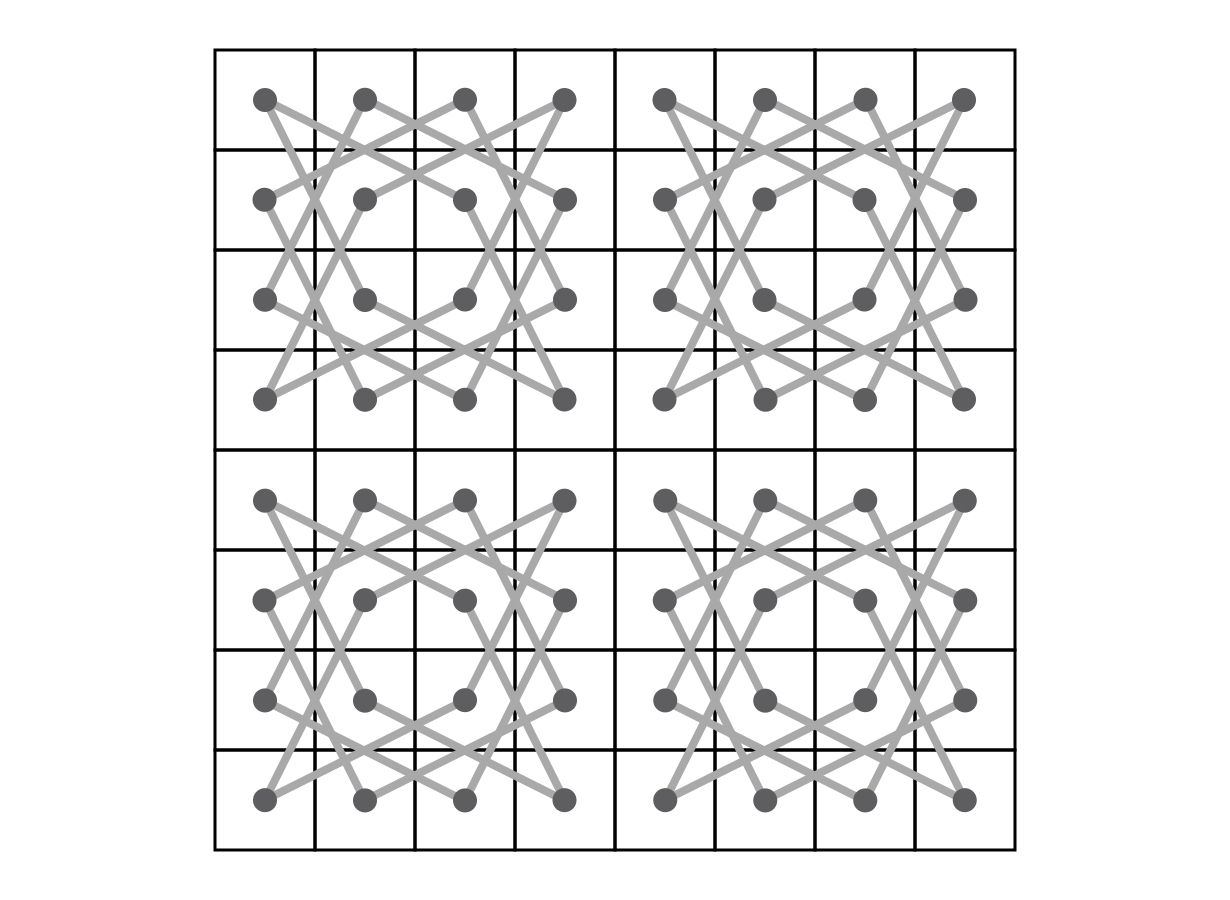
Ha a nagy körútba minden blokkból egy kis körutat szeretnénk, hogy kerüljön, akkor kiderül, hogy ez lényegileg egyféle módon tehető meg, ahogy azt az alábbi ábra mutatja.
Végül megemlíteném, hogy a kitűzött feladatnak egy speciális esete az, amikor megköveteljük, hogy a huszárok által bejárt terület egy élek mentén összefüggő tömb legyen, vagyis az a kérdés, hogy a sakktábla feldarabolható-e úgy négy (egyforma) összefüggő részre, hogy azok egy-egy huszárral bejárhatók legyenek. Ilyen verzióban ez a példa már megjelent egy több mint száz évvel ezelőtt kiadott nagyon híres feladványgyűjteményben, H. Dudeley: Amusements in Maths című könyvében a Dynamical chess puzzles című fejezetben. Akinek a megoldása nem ilyen volt, annak érdemes ezen is elgondolkodnia. A szóban forgó 339-es feladvány megoldása itt megtekinthető.