34. feladvány: Kollineáris mutatók

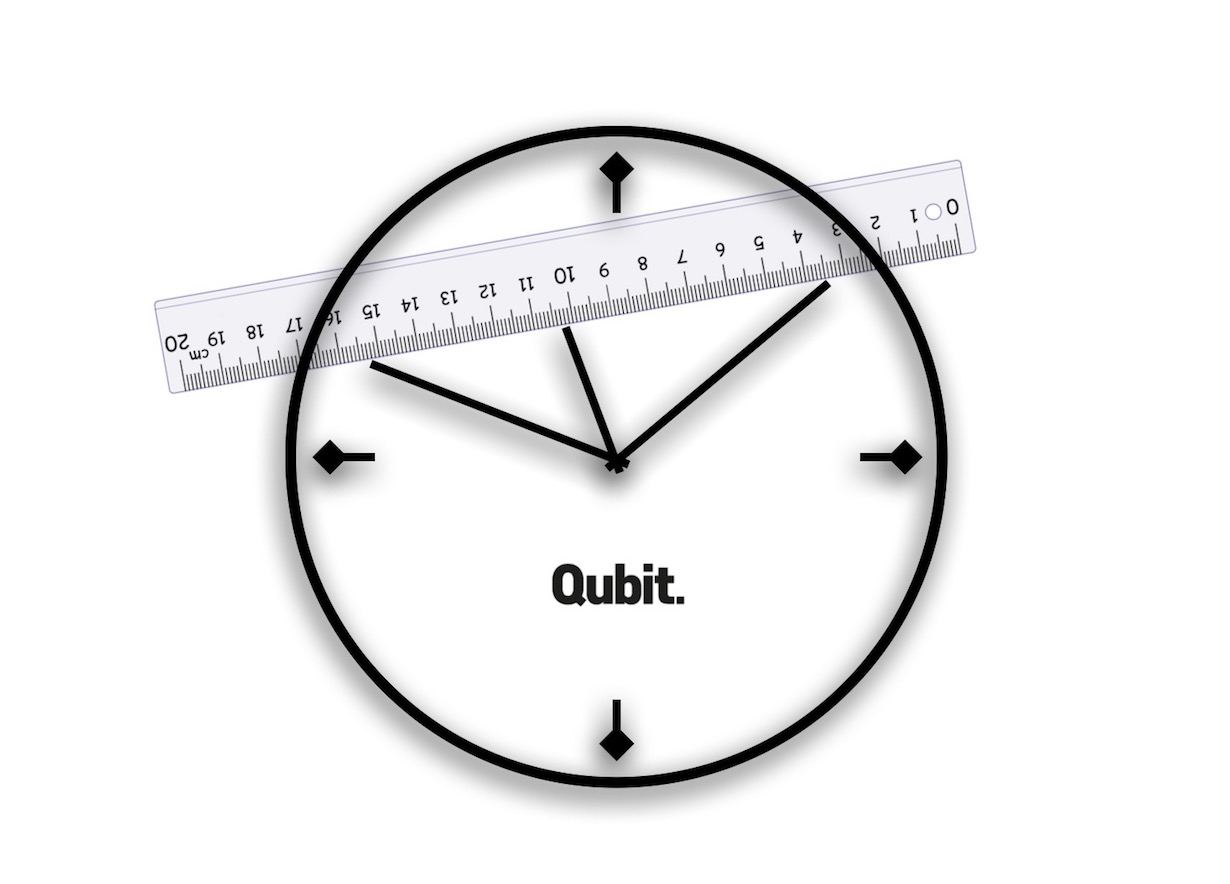
Van egy analóg 12 órás falióra, amelyik pontosan jár, van óra-, perc- és másodpercmutatója is, és mindegyik mutató folytonos mozgású, azaz egyenletes szögsebességgel járnak körbe. A perc- és másodpercmutatók hossza azonos, a kismutató azonban fele akkora, mint a másik kettő. Éjféltől számítva egy nap alatt hányszor fordul elő, hogy a három mutató végpontja egy egyenesre esik, de semelyik két mutató nem esik egymásra?

Felajánlott koponyák:

A megfejtéseket az eszventura@qubit.hu címre várjuk részletes magyarázattal együtt. A legelső és a legötletesebb versenyzők felkerülnek az Ész Ventura dicsőségfalára, közöttük és az egész évben legtöbb jó megoldást beküldők között év végén nyereményeket sorsolunk ki. Kérjük, leveleiket ékezetesen írják alá, álneveket is elfogadunk. Az e-mail subject mezőjében, kérjük feltüntetni, hogy 'megoldás', illetve sorszámmal jelezni, hogy melyik feladványról van szó. Beküldési határidő: október 15. éjfél.

Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus és bűvész