A LEGO-tornyos feladványban az volt a kérdés, hogy három építőkockából hányféleképpen lehet stabil tornyot építeni. Egy merev test egyensúlyának feltétele az, hogy a rá ható erők vektoriális összege, valamint bármely pontjára vonatkoztatva ezen erők által kifejtett forgatónyomatékok összege egyaránt zérus legyen. Mivel a testre ható gravitációs erő eredője a test tömegközéppontjában hat, az asztal által kifejtett kényszererő pedig csak a torony talapzatának pontjaiban tud hatni, ezért csak akkor lehet egyensúlyban a torony, ha tömegközéppontjának vetülete beleesik az alátámasztó felületbe, vagyis a legalsó elem(ek) közös alapterülete fölött helyezkedik el.

Stabil egyensúlyi helyzetről akkor beszélünk, ha piciny rázkódás vagy lökés hatására a torony nem dől fel. Ehhez a tömegközéppont vetületének szigorúan az alapterületen belül kell elhelyezkednie. Ha a vetület éppen a talapzat szélére esik, akkor piciny változás hatására kívül kerülhet, és ekkor már nem tudja a gravitációs erő forgatónyomatékát (például a korábbi alátámasztási pontra vonatkoztatva) az amúgy a gravitációs erővektorral éppen ellentétes irányú kényszererő ellensúlyozni, vagyis a torony feldől. Ebben az esetben beszélünk instabil egyensúlyi helyzetről.

Milyen tornyokat tudunk építeni?

Mindezek fényében vegyük sorra, milyen stabil tornyokat tudunk építeni. Nézzük először a háromemeletes tornyokat. A legegyszerűbb az egyenes torony, amiben közvetlenül egymás fölött helyezkednek el az építőelemek, lásd az alábbi ábrán bal fölül. Ez természetesen stabil. Az is mindenképpen stabil, amikor a három elemből kettő nem feltétlenül közvetlenül, de egymás fölött helyezkedik el, és csak a harmadik lóg ki, vagy oldalirányba, vagy egy sarok irányába rézsútosan. Ezekből összesen hat darab lényegesen különböző létezik, ezeket láthatjuk az ábra fölső sorában és még az alsó sor első két tornya is ide tartozik. Az illusztrációkat köszönjük Boros Péter megfejtőnknek.

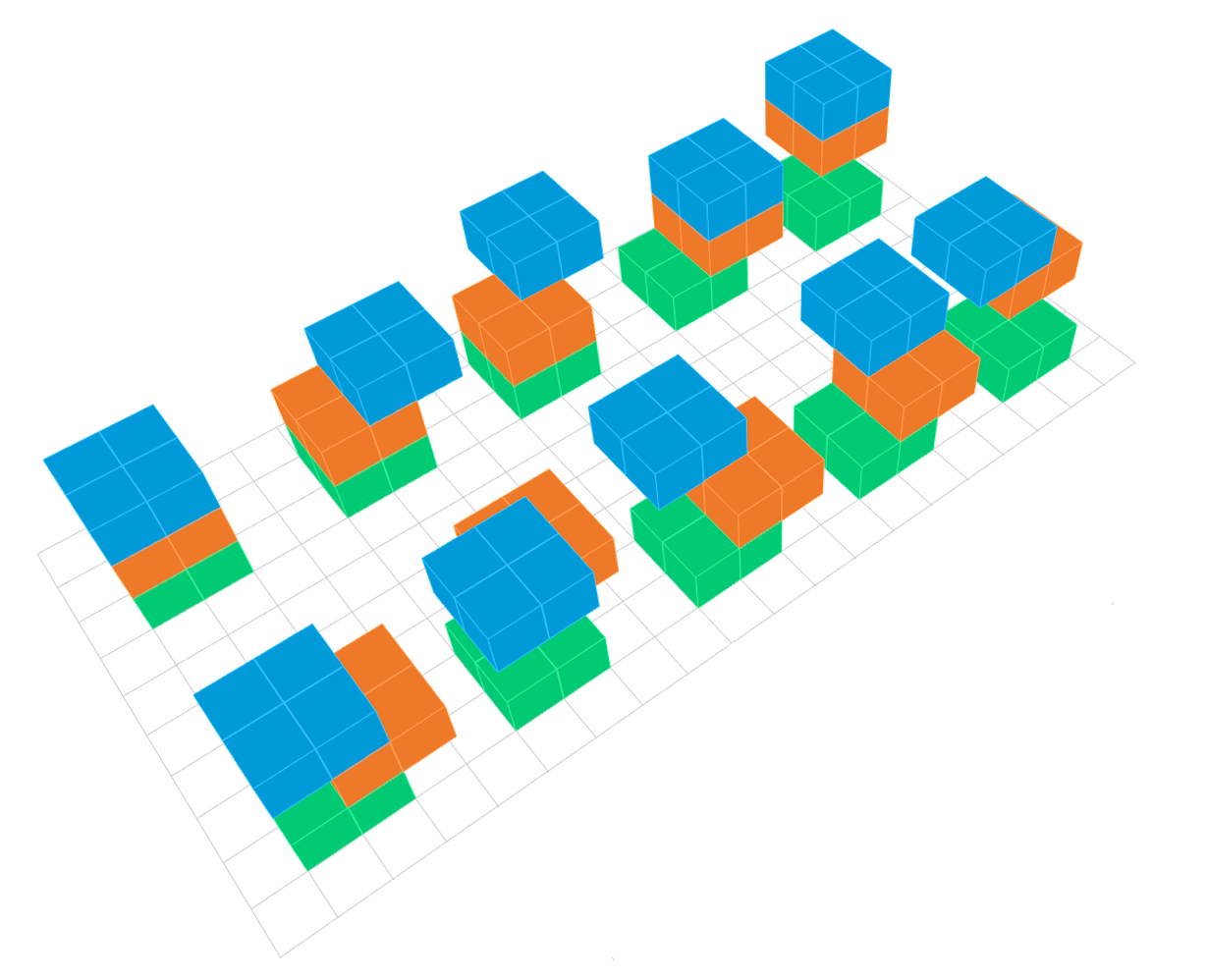
Ezen a ponton a háromemeletes tornyokra vonatkozóan érdemes az álábbi megállapításokat tenni. Egyrészt három építőelem felhasználásával nem tudunk olyan tornyot építeni, amely tömegközéppontjának vetülete a legalsó elem alapterületén kívülre kerülne, hiszen bármelyik irányba lépcsőzetesen távolodva lehet a tömegközéppontot legjobban eltávolítani az talapzat középpontjától, de így is csak annak a szélére kerülhet. Tehát legrosszabb esetben is csak instabil lesz az egyensúlyi helyzet. Egyébként pedig pontosan akkor lesz instabil, amikor a torony valamelyik oldaláról vett sziluettje lépcsőzetes, vagyis egy három lépcsőfokkal rendelkező lépcsőnek látszik oldalról.

Ezen megállapítások után nézzük azokat az eseteket, amikor semelyik két elem nincs egymás fölött. Ekkor a legalsó és a középső elem sincsen egymás fölött, így két eset lehetséges: vagy két bülyökkel, vagy egy bütyökkel érintkeznek. Nézzük sorra a két lehetőséget. Ha két bütyökkel érintkeznek, akkor a harmadik legfölső építőelem nyolcféle módon rakható a tetejére, mert négy sarka van a középső elemnek, amivel egy bütykön érintkezhet vele a legfölső, és négy éle van, amik mentén két bütyökkel érintkezhet, de figyelembe véve az egymásra szimmetrikus eseteket, meg azt, hogy ne kerüljenek egymás fölé elemek, valójában összesen csak négy lényegesen különböző elrendezés lehetséges. Ezekből kettő stabil és kettő instabil a fentebb megfogalmazott szabály szerint. A két stabil a fenti ábra alsó sorának 3. és 4. tornya.

Amikor a legalsó két elem csak egy bütyökkel érintkezik, a legfelsőt ugyancsak négy lényegesen különböző módon lehet ráhelyezni úgy, hogy ne essék egyik alatta lévővel se fedésbe. Most azonban ezek közül csak egy lesz stabil, lásd a fenti ábra alsó sorának utolsó tornyát; a másik három instabil.

Végül nézzük a kétemeletes elrendezéseket. Ezek lehetnek úgy, hogy kettő van alul és egy fölül, vagy egy alul és kettő fölül, de mindkét esetben teljesülnie kell annak a feltételnek, hogy az egyedül lévővel mindkét másik külön-külön érintkezik. Ez négyféle módon lehetséges, tehát összesen nyolc kétemeletes torony van, és ezek mindegyike stabil. Egy emeletes pedig nem lehet az építmény, mert a feladat kikötötte, hogy az elemeknek legalább egy bütyökben érintkezniük kell, ahhoz pedig különböző emeleten kell legyenek.

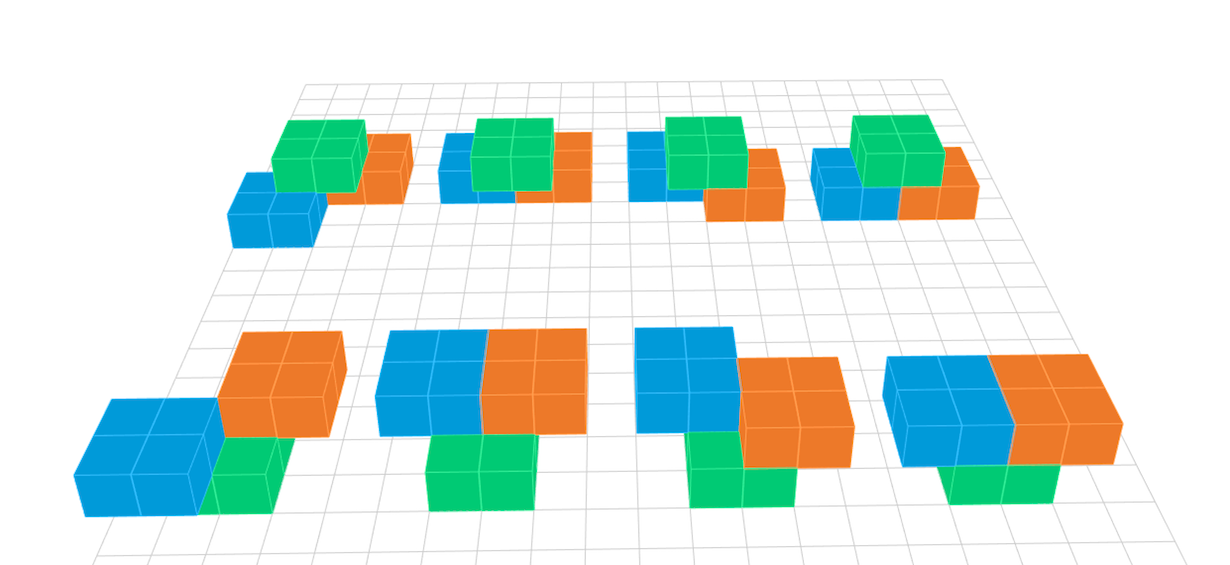
Összefoglalva: 10 háromemeletes stabil és 5 instabil torony van, továbbá 8 darab kétemeletes, amelyek mindegyike stabil. Öszsesen tehát 18 lényegesen különböző stabil torony építhető három LEGO-elemből.

Na és az instabil tornyok?

Végezetül térjünk egy kicsit vissza még az instabil tornyokra. Ha valaki kísérletezgetett, akkor tapasztalhatta, hogy az instabil tornyok kivétel nélkül mindig feldőlnek. Ez egy kicsit meglepő, hiszen ha az ember ügyesen kiegyensúlyozza, akkor egy pillanatra legalábbis meg kéne tudjon állni az instabil torony is. A magyarázat természetesen abban keresendő, hogy a valódi LEGO-építőelemek nem homogén téglatestek. Igen ám, de ha jobban belegondolunk, akkor a LEGO-elemek forgásszimmetrikusak, tehát a tömegközéppontjuk ugyanott van, mint ahol feltételeztük korábban, legfeljebb függőlegesen eltolódva, ez azonban a feldőlés szempontjából teljesen irreleváns.

Akkor hát mégis miért dőlnek el ezek a tornyok? A válasz az alátámasztási felületben rejlik, ugyanis a LEGO-elemek sarkai és élei picit le vannak kerekítve, és annyira pontosan gyártják már az elemeket, hogy az a pár tized miliméter is számít, az alátámasztási kényszererő ugyanis nem tud teljesen az elemek szélén hatni.

Ezen a héten lesz új feladvány is, de azt holnap, azaz kedden tűzzük majd ki. Figyeljétek a Qubitet!