33. feladvány: LEGO tornyok

Három darab 2×2-es Lego Duplo építőelemből összesen hányféle lényegesen különböző torony építhető, ami nem dől el?

Az elemek mindegyikének érintkeznie kell legalább egy bütykön keresztül egy másik elemmel. Az elemek nem állhatnak ferdén, vagyis bármely elem bármely oldalfala vagy párhuzamos, vagy merőleges kell legyen a többiek oldalfalaival, illetve oldalfalaira. A torony magasságára vagy a talapzat területére nincs megkötés, de az építménynek egy vízszintes sík lapon stabil egyensúlyban meg kell állnia úgy, hogy a síkkal érintkező elemek teljes alapjukkal érintkeznek. A lényegesen különböző azt jelenti, hogy forgatással vagy tükrözéssel sem transzformálhatók egymásba. Továbbá az illusztrációval ellentétben a színek sem számítanak, vagyis az elemeket nem tekintjük megkülönböztethetőknek.

Figyelem, ez egy matematikai és fizikai feladvány egyben, amihez a kísérletezés segíthet, de elméleti indoklást várunk. Az elméleti indoklásban az építőkockákat tekinthetjük homogén sűrűségű tömör négyzet alapú egyenes hasáboknak, amelyek össze vannak ragasztva.

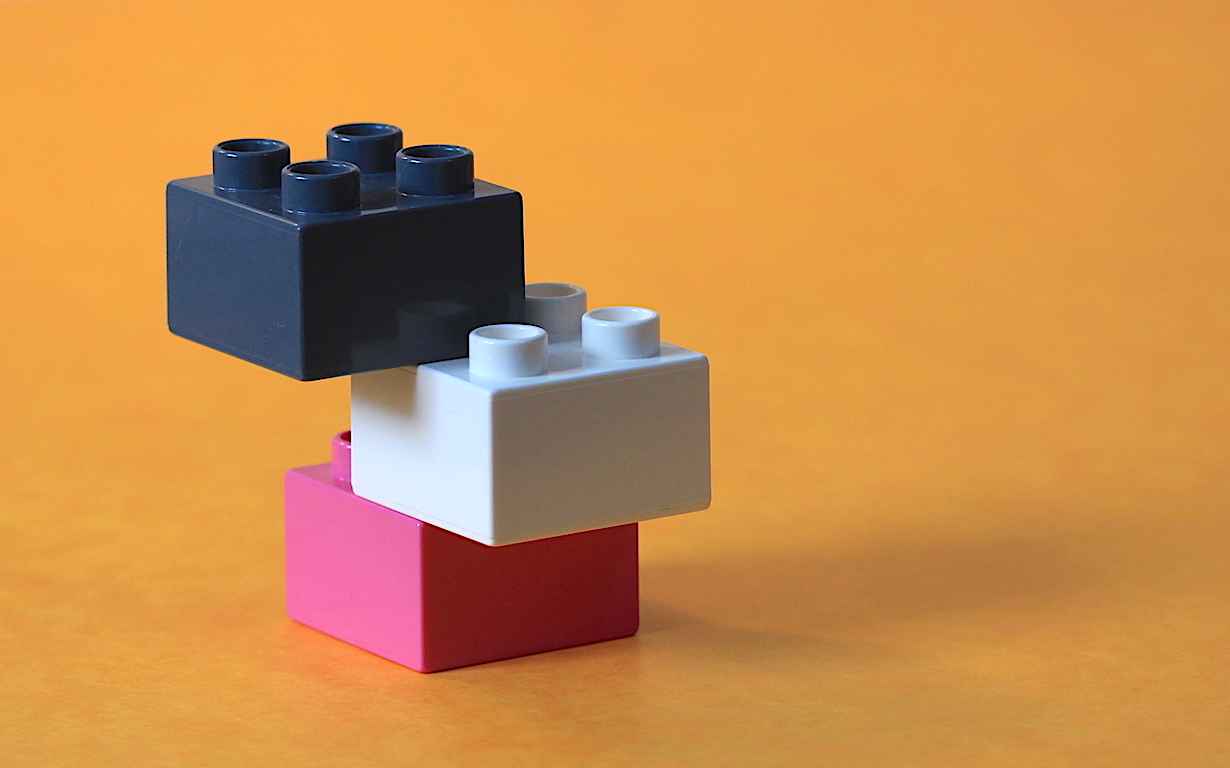
Felajánlott koponyák:

A megfejtéseket az eszventura@qubit.hu címre várjuk részletes magyarázattal együtt. A legelső és a legötletesebb versenyzők felkerülnek az Ész Ventura dicsőségfalára, közöttük és az egész évben legtöbb jó megoldást beküldők között év végén nyereményeket sorsolunk ki. Kérjük, leveleiket ékezetesen írják alá, álneveket is elfogadunk. Az e-mail subject mezőjében, kérjük feltüntetni, hogy 'megoldás', illetve sorszámmal jelezni, hogy melyik feladványról van szó. Beküldési határidő: október 5. éjfél.

Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus és bűvész