Azt gondoltam, lassan közelíteni kellene egymáshoz ennek a rovatnak a témáit, a nyelvet, a gépet és az embert. A nyelvhasználathoz intelligencia szükséges, ezért a nyelvészeti modelleknek tartalmazniuk kell az intelligencia modelljét is (vagy legalábbis hivatkozniuk kell rá). Ha azt akarjuk, hogy a számítógépek utánozzák a nyelvi viselkedésnek legalább bizonyos fajtáit (például hogy társalogjanak vagy fordítsanak), akkor olyan modellekre van szükségünk, amik számítógépes programok alakjában is megvalósíthatók. Ezért a modelljeinkbe épített intelligencia-modellnek is ilyennek kell lennie – az ilyen modelleket összefoglalóan mesterséges intelligenciának nevezzük. És ha már beszélünk róluk, próbáljuk meg programok formájába is önteni.

Manapság divatkifejezés lett a mesterséges intelligencia (meg a gépi tanulás és hasonlók). Nagyon sok mindent neveznek így, lényegében bármilyen programot, ami olyan döntések meghozatalára képes, amilyet az emberek is meghoznak, és ehhez az intelligenciájukat használják. De csak azokat a döntéseket vesszük ilyenkor figyelembe, amik valahogy nem mechanikus szabályok alkalmazásával születnek. Például egy kalkulátor (számológép) képességeit nem tekintünk mesterséges intelligenciának, mert bár a számoláshoz intelligencia kell, valahogy túl egyszerűek a szabályai. Hogy pontosan hol kezdődik a mesterséges intelligencia, azt nehéz megmondani, de például már oda szoktuk sorolni azt, amikor a vásárlási szokásaink megfigyelése után egy program arról dönt, hogy milyen reklámokat mutogasson nekünk. Ehhez ugyanis a programnak rengeteg adatból, amiket a korábbi vásárlásainkról, vagy legalább termékek és szolgáltatások iránt mutatott érdeklődésünkről gyűjtöttek, meg ezeknek a termékeknek és szolgáltatásoknak a jellegéből ki kell alakítania („meg kell tanulnia”) a vásárlói profilunkat, és ez nem nagyon egyszerű feladat.

Hogy aztán ezt a profilozást a szó hétköznapi értelmében tényleg intelligens viselkedésnek nevezhetjük-e, az filozófiai kérdés, ezért nem is foglalkozom vele. Enélkül is elég bajunk lesz azzal, hogy valahogy rendet vágjunk a mesterséges intelligenciának nevezett sokféle modell között, vagy hogy legalább néhányat közelebbről megnézzünk.

Kezdetben volt a tudásbázis

A kérdés történetéről annyit, hogy – ahogy egy korábban itt megjelent írásban már utaltam rá – az 1980-as évekig az intelligenciának elsősorban a logikai aspektusát próbálták modellálni. Vagyis úgy képzelték az intelligenciát, mint egy hatalmas tudásbázist (rengeteg állítás összességét), plusz néhány logikai képességet, amiket szabályokba lehet foglalni (ilyen képesség elsősorban a következtetés). Például az orvosi intelligencia modelljeiben mindenféle betegségekről, biokémiai és fizikai folyamatokról stb. származó állítás szerepelt, és ha feltették nekik azt a kérdést, hogy egy konkrét beteg konkrét vizsgálati eredményei alapján milyen kúra lenne indokolt, akkor az algoritmus a tudásbázisából következtetések levonásával próbált erre választ adni.

Az 1980-as évektől (igazából már korábban, ahogy ez lenni szokott az ilyen történeteknél) fokozatosan egészen más megközelítésre tértek át a tudósok. Az orvosi példánál maradva: az a nézet lett uralkodó, hogy az orvosok egyáltalán nem logikai következtetéseket használnak a gyógyításban. A tudásbázisuk nem természeti törvényekből meg általános jelenségek leírásából áll, hanem rengeteg konkrét tapasztalatból, egyes betegek sorsáról (a tüneteikről, a kezeléseikről és azok eredményeiről). Minden új esetet úgy értékelnek, hogy összevetik a régi tapasztalataikkal, és ha találnak hozzá hasonlókat, akkor megpróbálnak olyan kúrát választani, ami aszerint a leggyakrabban a legjobbnak minősült. Ez a megközelítés tehát nem annyira a logikai képességeket tekinti intelligenciának, hanem a hasonlóságok keresését, valamint a megtalált hasonló esetekből egy új megoldás szintetizálását. Abban a bizonyos korábbi írásomban ezt a felfogásbeli változást paradigmaváltásnak neveztem, és azt állítottam, hogy a nyelvről alkotott elképzeléseinkben is kezd végbemenni, és egyre nagyobb sikere van.

Persze az első lépéseket nem olyan bonyolult területen tették meg, mint az orvosi tudás (annak a modellálása talán még ma is csak science fiction). Bár első hallásra furcsának tűnhet, a számítógépes karakter- (betű- és számjegy-) felismerés ugyanolyan természetű, csak egyszerűbb probléma, mint az orvosi szaktudás. Nagyon bonyolult az összefüggés egy-egy betű vagy számjegy rengetegféle kézzel írt változata és az ábrázolt „ideális” (pl. nyomtatott) betű vagy számjegy között. Annyira bonyolult, hogy szabályokba foglalni szinte reménytelen. (Például nagyon kevés konkrét esetben igaz az, hogy az o betű egy szögletekkel nem rendelkező, önmagába visszaérő vonal, de még az sem lenne elég, ha megengednénk, hogy „egy kicsit” megszakadjon, mert akkor nehéz lenne a c betűtől megkülönböztetni.) Azok a számítógépes programok, amik sikeresen ismerik fel a betűket és számjegyeket, nem szabályokat alkalmaznak, hanem egy tudásbázist tartalmaznak, amiben rengeteg konkrét leírt betű és számjegy emlékét őrzik (a megfejtéseikkel együtt), és ezekhez hasonlítják az új, felismerendő adatokat, ugyanúgy, ahogy a doki a korábbi tapasztalataival veti össze azt, amit az új betegnél tapasztal.

Az első felismerő programok (például a Magyar Posta által 1978-ban megvásárolt gépsor, ami elég nagy biztonsággal ismerte fel a borítékokon az irányítószámokat) még nem így működtek, és nem sok közük volt a mesterséges intelligenciához. Az 1980-as évek elejéről-közepéről származnak az utolsó simításai azoknak az algoritmusoknak, amiket ma is használunk, és amiknek már tényleg az az alapjuk, hogy a korábbi tapasztalatokból megtanulják a betűk, számjegyek stb. felismerését. Ez volt az első nagy, és nagyon látványos ugrás az újfajta mesterséges intelligencia fejlődésében. De az orvosi tudás esetében ez a képesség, a felismerés képessége még csak valami diagnózisféle felállításának felel meg, a gyógyítástól még messze vagyunk.

Hogyan működik a felismerés?

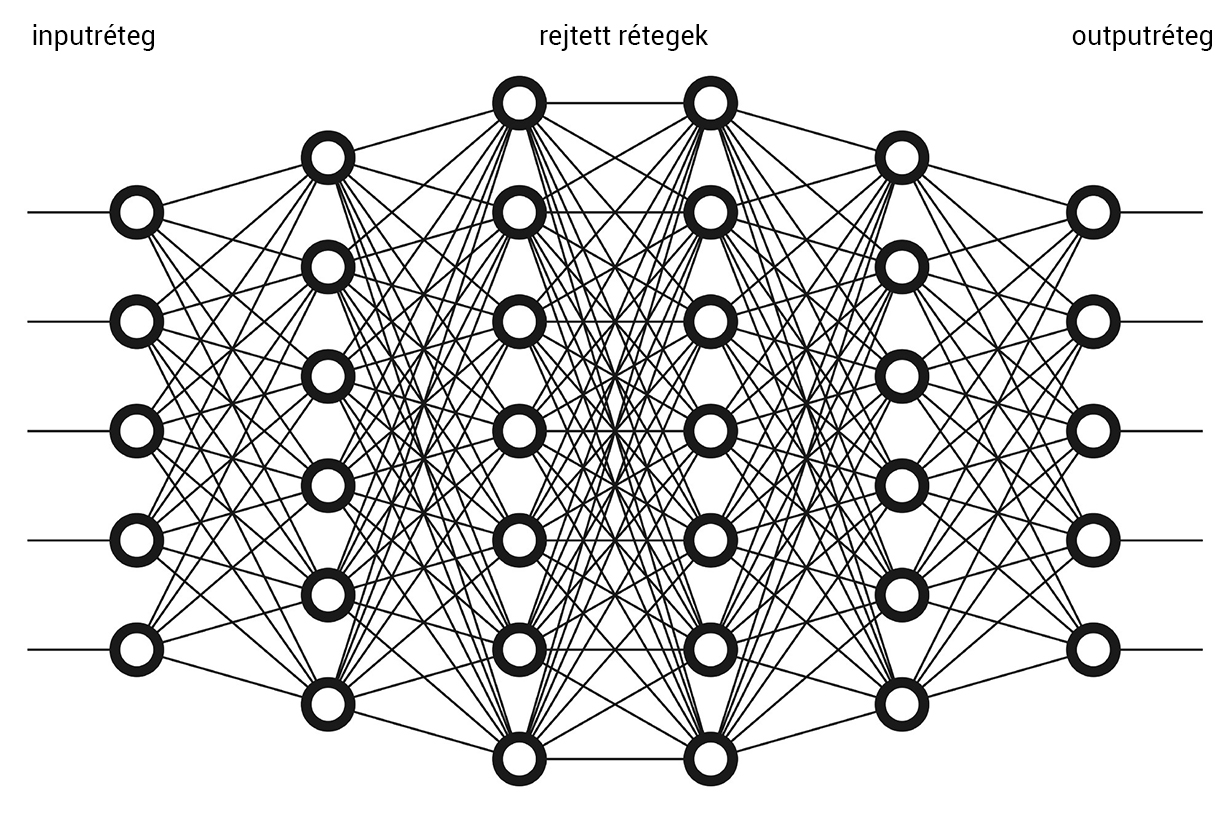
A ma leghatékonyabban működő felismerő algoritmusok a rengetegféle gépi tanulási módszer közül azt használják, amit neuronhálók segítségével lehet a legjobban szemléltetni (neuronális vagy neurális hálóknak is nevezik őket). Ezek a hálózatok sok egyforma apró (és önmagában elég buta) elemből állnak, ezek a (mesterséges) „neuronok”. Az idegrendszer neuronjairól mintázták őket, de azoknál jóval egyszerűbben működnek – hogy igazából mennyire hasonlít a mesterséges neurális hálók működése az idegrendszerére, ahhoz nem értek, és a szempontunkból nem is érdekes. A neuronok rétegekbe vannak rendezve: minden neuronnak van egy csomó bejövő kapcsolata, amik tipikusan az előző rétegből indulnak (onnan szállítanak ingereket), és van egy kimenete. Csak egy kimenő ingerről beszélünk, de ez az inger a következő réteg összes neuronjához eljut azoknak a bejövő kapcsolatain keresztül. A neuron nem csinál mást, mint a hozzá beérkező ingereket összegzi: összeadja, és az összegre alkalmaz valamilyen függvényt, ennek az értéke a kimenő inger. Nagyon sokféle lehet egy neurális hálózat, de annyi mindegyikben közös, hogy kitüntetett szerepe van a legelső, input- és a legutolsó, output- rétegnek. Az inputréteg ingerlésével tápláljuk be az adatokat (amiből a hálózatnak tanulnia kell), valamint a tanulás után a felismerendő adatot is; az outputréteg állapotáról olvashatjuk le, hogy hogyan reagált a bemenő adatra a hálózat.

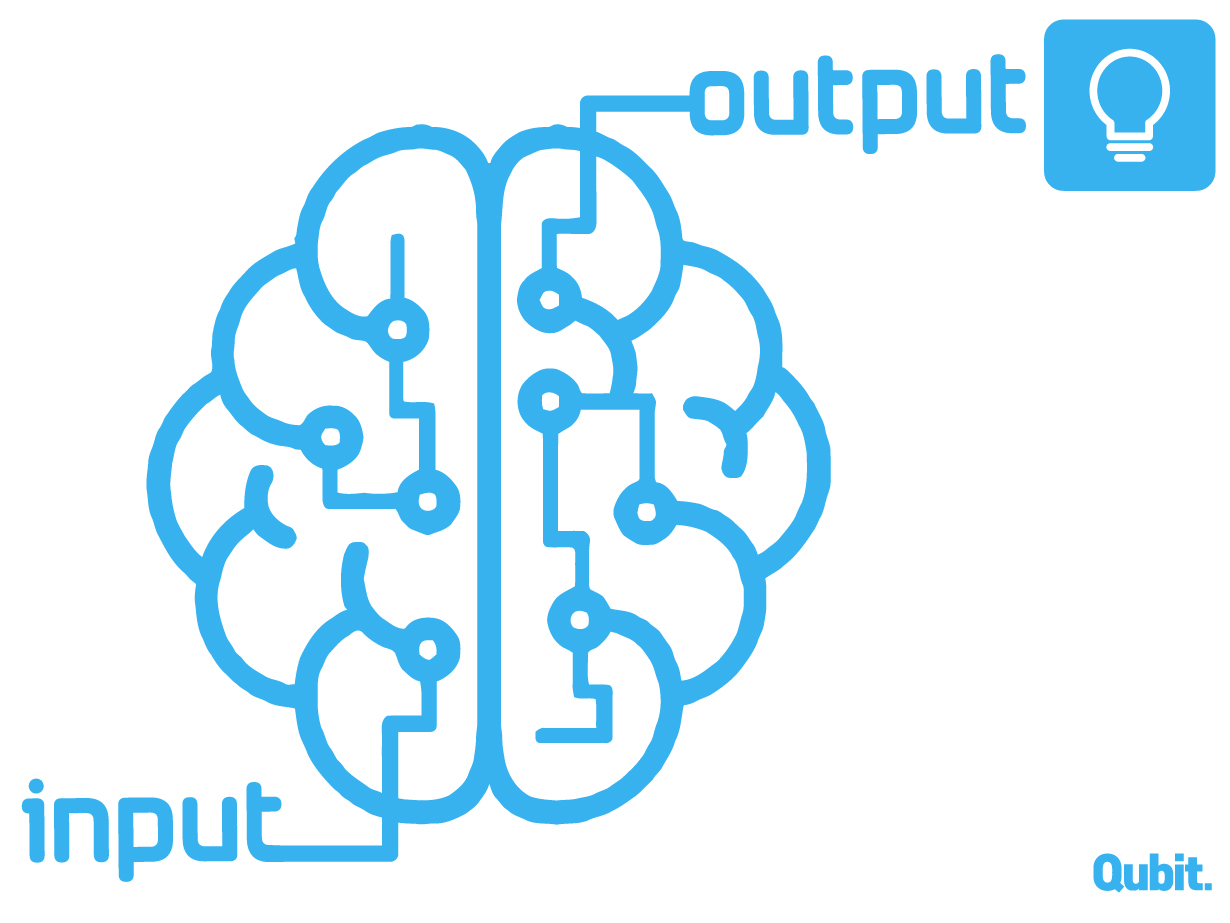
Azok a neurális hálók, amikről itt szó lesz, ún. felügyelt (supervised) tanulás révén tesznek szert a felismerőképességükre. Ez azt jelenti, hogy rengeteg adatot „mutatunk” nekik egymás után (úgy, hogy az inputrétegük neuronjait ingereljük), olyanokat, amiknek ismerjük a „megoldását”. Például olyan kézzel írt számjegyek képét (pixelekre bontva), amikről tudjuk, hogy milyen számot akarnak jelenteni. A megoldásokat az outputréteg neuronjainak aktivitásában várjuk. Például ha tíz lehetséges számjegy van, akkor az outputréteg állhat tíz neuronból; azt várjuk, hogy ha 1-es számjegyet „mutatunk” a hálózatnak, akkor az az output-neuron váljon nagyon aktívvá, amit mi az 1-nek megfelelőnek kiáltunk ki. Kezdetben persze teljesen véletlenszerű értékeket fogunk kapni az outputréteg neuronjain, de ez a tanítás során változni (javulni) fog. Ezt a fajta tanulást azért hívjuk felügyeltnek, mert a kezdeti rossz értéknek megfelelően módosítjuk a hálózatot (mintegy „megbüntetjük” a hibás eredményért, és megmutatjuk neki, mit kellett volna másképp csinálnia). Az eredmények így egyre jobbak lesznek, és a hálózat sok-sok ismétlés után már magabiztosan meg tudja oldani a felismerési feladatot.

A neuronhálónk részletesebben

Innentől csak annak érdemes tovább olvasni az írást, akit egy kicsit részletesebben érdekel, hogy hogyan történik a mesterséges felismerés csodája (természetesen mesterséges tanulás útján). A valóságban sokféle neuronhálózat és tanulási módszer létezik: Sokfélék lehetnek a neuronok, a rétegek, a kapcsolatok. Sokféle lehet a neuronra jellemző függvény is. A sokféle lehetséges neuronhálózat és tanulási módszer közül az egyik nagyon elterjedt fajtáról fogok beszélni, és csak néha utalok arra, hol lehetnek ettől eltérések.

Vegyük például azt a feladatot, hogy majom- és emberarcokat ábrázoló fényképeket kellene megkülönböztetnünk egymástól: majmot, vagy embert ábrázol a kép? Az egyszerűség kedvéért tegyük fel, hogy csak fekete-fehér képeink vannak, és mindegyik egyforma nagyságú, mondjuk vízszintesen n, függőlegesen pedig m pixelnyi. Vagyis az egész kép n * m pixelből áll. Ennyi neuronból kell tehát állnia az inputrétegnek. Az egyes pixelek színe valahol a fehér és a fekete között van, ezt leírhatjuk egy-egy 0 és 1 közötti számmal – ezekkel a számokkal ingereljük az inputréteg egyes neuronjait (vagyis az inputréteg neuronjainak nincs mit összegezniük, eleve az összeget kapják meg tőlünk ingerként). Úgy fogjuk alakítani a dolgot, hogy a neuronok által kibocsátott ingerek (amit úgy is hívunk, hogy a neuronok aktivációja, aktivációs szintje) szintén egy 0 és egy közötti szám legyen.

Ehhez a feladathoz elég, ha az outputréteg egyetlen neuront tartalmaz, hiszen mondjuk elhatározhatjuk, hogy ennek az aktivációs szintje legyen (majdnem) 0, ha majomarcot „mutatunk” az inputrétegnek, és legyen (majdnem) 1, ha emberarcot (vagy fordítva). Az input- és az outputréteg között legyen még egy vagy több ún. rejtett réteg – hogy hány ilyenre van szükségünk, és hogy hány neuronból álljanak, azt elég nehéz meghatározni, és általában nincs is túl nagy jelentősége, ez a finomhangolás része.

A neuronra jellemző aktiváció-kiszámító függvény is sokféle lehet, például olyan egyszerű is, hogy az összegzett ingereket összehasonlítja egy küszöbértékkel, és nem tüzel (0 a kimenő inger), ha az összeg nem éri el a küszöböt, illetve tüzel (1 a kimenő inger), ha eléri. De mi vegyünk egy divatos és praktikus ún. szigmoid függvényt, ami onnan kapta a nevét, hogy egy kicsit az S betűre emlékeztet az alakja: az értéke lassan indul felfelé, majd gyors növekedésbe kezd, végül laposan közelíti meg a felső határértékét. (Hasonló okokból használják ezt, mint a gyakoriságok esetében a logaritmust, ld. az erről szóló korábbi írásomat.) A legegyszerűbb szigmoid függvény képlete: y = e^x/(1 + e^x). Ezzel le is írtuk azt, hogy mi történik, amikor az inputréteg neuronjait majom- és emberképekkel ingereljük.

A tanulási fázis

A tanulás mindenképpen változást jelent: amikor megtanultunk valamit, akkor mások lettünk, mint amilyenek előtte voltunk. Ez azt jelenti, hogy a neuronális hálózatunknak is változnia kell a tanulás során – hogy mi fog változni, arról eddig nem szóltam, de mindjárt elárulom. A tanulás úgy történik, hogy minden egyes ingerlési fázis után (miután „mutattunk” egy képet az inputrétegnek), következik egy tanulási fázis, amit az vezérel, hogy mekkora aktiváció jelent meg az outputréteg neuronjain (és hogy azok mennyire tértek el az általunk ismert helyes választól).

A példánkban, ha majomarcot mutattunk, és túl nagy az output-neuron aktivációja (pedig 0 közeli számot vártunk eredményként), akkor ennek megfelelően változtatunk valamit a hálózaton, és megfordítva, ha emberarcra túl kicsi aktivációs értéket kapunk (pedig 1 közelinek kellett volna lennie), akkor az ellenkező irányban változtatjuk a hálózatot. Ezt jó sokszor megismételve azt fogjuk tapasztalni, hogy egyre kevesebbet kell változtatnunk, egyre jobb lesz a felismerés eredménye. Nem tudjuk pontosan megmondani, hogy milyen „szabályokat” tanult meg a hálózatunk, de valamit biztosan, mert egyre jobb a felismerési képessége.

Valójában az történik, hogy a majomarcok tényleg különböznek az emberarcoktól, vagyis van összefüggés, függvénykapcsolat a bemenet (a pixelek) és a kimenet (a 0-hoz vagy 1-hez közelítő szám) között, csak éppen ez az összefüggés rettentő bonyolult. A hálózatunk tanulási folyamata matematikai értelemben nem más, mint ennek a bonyolult függvénynek a fokozatos közelítése. Vagy másképpen megfogalmazva: a tanulás során a jó megoldástól való eltérést (az ún. hibát) próbáljuk minimálisra csökkenteni. A hiba mértékét is egy függvénnyel adhatjuk meg, és annak a függvénynek az értéke is mindig a hálózatból fakad valahogy. Úgy kell változtatnunk a tanulás során a hálózatot, hogy ennek a függvénynek a minimumát (pontosabban: valamelyik minimumát) találjuk meg.

Rövid megjegyzés: Elképzelhető, hogy a hálózat nem a lehető legkisebb minimumot találja meg, hanem egy másik, kevésbé kicsit. Ez olyan, mintha le akarnánk menni a hegyről a völgyben fekvő városba, ezért elindulunk lefelé, de a város helyett egy magasabban fekvő, lakatlan völgyben kötünk ki. Ez a gyakorlatban nagy probléma lehet, de nem fogunk vele foglalkozni, mindig lefele próbálunk majd menni, még akkor is, ha a várost sosem érjük el. Vannak technikák arra, hogy jobb eséllyel találjuk meg az utat a városig (esetleg még azon az áron is, hogy néha egy kicsit felfelé kelljen kapaszkodni), de ezekkel most nem foglalkozunk.

Nos, akkor mi változzon a tanulás során? Azt szokták feltételezni, hogy maguk a neuronok (vagyis az a függvény, amit az összegzéskor alkalmaznak) nem változnak, azok mind egyformák. Amit változtatni tudunk, az a kapcsolatok erőssége, súlya, vagyis hogy mennyire tompítják azt az ingert, amit közvetítenek. (Minél erősebb egy kapcsolat, annál kevésbé tompít.) Az egyes kapcsolatok erősségét egy-egy számmal jellemezzük, amivel megszorozzuk az érkező inger nagyságát. Az a neuron, ahova az inger beérkezik, ezek szerint nem egy sima összeget, hanem egy súlyozott összeget fog feldolgozni. (Bonyolultabb hálózatokban még más dolgok is változhatnak a tanulás során, például olyan értékek, amik az egyes rétegekre jellemzőek, de ez is inkább a finomhangolás része.) Ezek után a kérdés már csak az, hogy miként változtassuk a súlyokat attól függően, hogy mennyire tetszik a hálózat döntése egy-egy kép megmutatásakor (vagyis hogy éppen mekkora és milyen irányú a hiba).

Valósítsuk meg!

Az írásom innentől inkább csak azokat fogja érdekelni, akik maguk is mesterséges felismerést akarnak játszani, vagyis neurális hálós programot akarnak írni. A gyakorlat kedvéért majd érdekes lesz programozási részéről is beszélni, de egyelőre tisztázzuk a tanulás algoritmusát.

A tanulási folyamat legelterjedtebb, legnépszerűbb módszere az, amit a szakirodalom visszafele terjedésnek (backpropagation) nevez. Arról van szó, hogy az outputrétegtől a hálózatban visszafelé haladva nyomon kell követnünk, hogy melyik kapcsolat mennyire felelős a hibákért, vagyis az output-neuronokon megjelenő aktiváció és a várt eredmény különbségéért, és ennek megfelelően kell módosítani a súlyokat, hogy a következő körben már egy kicsit jobban viselkedjenek. Ennek a visszakövetésnek első látásra egy kicsit bonyolult a matematikája, ettől meg is fogom kímélni az olvasót (amúgy millió helyen megtalálható a neten a részletes magyarázatuk, nagyon sokféleképpen és sokféle közönség számára). Tulajdonképpen egyszerű algoritmusról van szó, ezért ma már egy néhány soros programmal mi magunk is tudunk olyan virtuális gépet fabrikálni, ami sokszorosan jobb az irányítószámok felismerésében, mint az 1978-ben Magyarországon üzembe helyezett gépek. (Azoknak a szíve egy olyan számítógép volt, aminek 64 kilobyte volt a központi memóriája!)

A lényeg az, hogy az output-réteg neuronjainál a hibát egyszerűen úgy számoljuk ki, hogy 2-vel megszorozzuk az elvárt érték és a tényleges aktiváció különbségét (hogy miért így, arra most nem térek ki). Az odaérkező kapcsolatok súlyát pedig a következő értékkel növeljük: az előző neuronnak (ahonnan a kapcsolat érkezik) az aktivációját megszorozzuk a hibával és azzal a számmal, amit úgy kapunk, hogy az output-neuron aktivációját megszorozzuk egy függvény értékével az output-neuron aktivációjának helyén. Hogy mi ez a függvény? Nem más, mint neuron számolófüggvényének (esetünkben a szigmoid függvénynek) a deriváltja. (Ha a számolófüggvény a fenti szigmoid függvény, akkor a deriváltjának a képlete: y = x *(1 – x).) Hogy mi a szerepe itt a deriválásnak, abba szintén nem megyek bele részletesen. Legyen elég annyi, hogy a (részleges) deriválással pont azt tudjuk kifejezni, hogy azoknak az adatoknak az apró változása, amiktől a függvény értéke függ, milyen módon befolyásolják a függvényérték változását.

Tulajdonképpen ennyi az egész; még azt kell tudni, hogy a belső neuronok esetében a hibát bonyolultabban kell számolni: meg kell nézni, hogy milyen kapcsolatok vezetnek a következő réteg neuronjaihoz, azoknak a súlyát meg kell szorozni egyenként azoknak a következő neuronoknak a hibájával, és ezeket össze kell adni. Vagyis ez ugyanolyan súlyozott összeg, mint amit az ingerület előrefelé terjedésénél (az inputrétegtől az outputréteg felé) láttunk. Innen kapta a nevét az egész algoritmus, ezért becézik visszafelé terjedésnek.

És hogy kell ehhez programot írni?

Ami a programozási részt illeti, ott elsősorban azt kell eldöntenünk, hogy hogyan ábrázoljuk a hálózatot a virtuális világunkban. Sokféleképpen csinálhatjuk, de alapvetően két irányt tudok elképzelni. Az egyik irány az „elvontabb”, kevésbé szemléletes, ami viszont valószínűleg hatékonyabb. Azért nevezem elvontabbnak ezt az ábrázolást, mert itt nem felelnek meg külön lények a neuronoknak meg a kapcsolatoknak, ezeket csak egy-egy számmal jellemezzük (a neuronokat az aktivációjukkal, a kapcsolatokat a súlyukkal). Egy-egy réteg nem más, mint ilyen aktivációkból álló tömb, a rétegek közötti kapcsolatok szintén számokból (súlyokból) álló tömbök. (Az i-edig réteg és az i + 1-edik réteg közötti kapcsolatok száma az i-edik réteget alkotó neuronok száma megszorozva az i + 1-edik réteget alkotó neuronok számával.)

Ha kevésbé elvont ábrázolásra vágyunk, akkor minden neuront és minden kapcsolatot (és persze minden réteget) egy-egy virtuális lénnyel ábrázolunk. Ha akarjuk, a neuronokra mint lényekre nemcsak az aktivációjuk lesz jellemző, hanem a bejövő kapcsolataik és (vagy) a következő réteghez menő, tőlük kiinduló kapcsolatok is. Hasonlóképpen a kapcsolatokban számon tarthatjuk nemcsak az erősségüket (súlyukat), hanem azt is, hogy melyik neurontól melyikhez vezetik az ingerületet. Ez az ábrázolás több adminisztrációt igényel, mint az elvontabb (bonyolultabbak a lényeink), de szemléletesebb, és sok számítást egyszerűbbé tehet.

Minden mást, amit feljebb az ingerület (előre) terjedéséről és a tanulási folyamatról leírtam, már meg tudunk valósítani azokkal a programozási eszközökkel, amiket korábban elmagyaráztam. Talán még egy fogalomról illene szót ejtenem, ami hasznos lehet a feladat megoldásában: a struktúrákról.

Struktúrák

A struktúrák nagyon hasonlítanak a tömbökre annyiban, hogy több egymással összefüggő adat egy helyen való tárolására szolgálnak (sokszor valóban úgy valósítják meg őket, hogy a memória egyetlen összefüggő területét foglalják el). Egy fontos különbség van: míg a tömbök ugyanolyan típusú lények sorozatai, addig a struktúrák mindenféle típusú lényeket tartalmazhatnak, de előre meg kell adni, hogy milyeneket. Például a neurális hálózatunkban egy-egy kapcsolatot ábrázolhatunk olyan struktúrával, ami tartalmaz egy tizedes törtet (a kapcsolat súlyát), meg két neuront (ahonnan és ahova a kapcsolat vezet) – akármivel ábrázoljuk is ezeket a neuronokat. A kapcsolat mint struktúra tehát olyan adattípus lenne, aminek három tagja van, és ezeknek nevet is kell adnunk (pl. suly, innen és ide), és a típusukat is meg kell előre határoznunk. (Aki emlékszik még arra, amit az osztályokról írtam, az észre fogja venni, hogy az osztályok, bár sokkal bonyolultabb dolgok, játszhatják a struktúrák szerepét is. Ott a kártyapakli egy-egy lapjának típusa egy osztály volt; struktúra is lehetett volna.) A struktúrákat régebbi programozási nyelvekben rekordoknak is nevezik. Itt van például egy lehetséges struktúra, ami a kapcsolatok típusát ragadja meg, C nyelven:

typedef struct
{
unsigned int innen;
unsigned int ide;
float suly;
} Kapcsolat;

Itt feltételeztük, hogy a neuronjainknak sorszámuk van, tehát a két neuront, amit a kapcsolat összeköt (innen és ide), egy-egy nem-negatív egész számmal (unsigned int) azonosítjuk; a float a C nyelvben a (32 biten tárolt) tizedestörtek típusa.

Ha a hálózatok kevésbé elvont ábrázolását választjuk, és külön-külön lény lesz minden neuronunk és kapcsolatunk, akkor valószínűleg szükségünk lesz arra, hogy az egyik lényben tárolt információ utaljon más lényekre. Például úgy, ahogy a fenti Kapcsolat struktúra két tagja utal neuronra (az innen és az ide). Ugyanígy a neuronok tulajdonságai között szerepelhetnek a bejövő és kiinduló kapcsolataik. Ezt többféleképpen is megoldhatjuk, például úgy, ahogy a Kapcsolat struktúrában, hogy (rétegenként vagy globálisan) beszámozzuk az összes neuronunkat meg kapcsolatunkat, és ezekkel a sorszámokkal azonosítjuk őket. Egy másik megoldás az, hogy a memóriacímeiket használjuk az azonosításukra, úgy, ahogy azt egy korábbi írásban elmagyaráztam.Annak ugyanis semmi akadálya, hogy a struktúráink tagjai között legyenek memóriacímek (mutatók) is. Ez persze nagy elővigyázatosságot igényel, hiszen csak annak van címe, amit korábban már létrehoztunk, és csak addig tudjuk használni a címét, amíg még létezik. De ez már csak távolabbról függ össze azzal, hogy hogyan működik az automatikus felismerés, ezért külön fogunk majd beszélgetni róla.

A szerző nyelvész, az MTA Nyelvtudományi Intézetének főmunkatársa. A Qubit.hu-n megjelent írásai itt olvashatók.