Ész Ventura: Hogyan segít ez a színkavalkád az almacsutkába írt kör esetében?

A 42. feladványban azt kellett megmutatni, hogy az egybevágó negyedkörök által határolt almacsutkába írt legnagyobb körök éppen érintik egymást, ahogy az alábbi ábrán is látható. Aki lusta számolni egy Pitagorasz-tételnyit, az görgessen lejjebb a nagyon-nagyon színes ábrához!

Vegyük észre, hogy az almacsutka két domború negyedköre ugyanannak a nagy körnek két köríve. A bizonyítandó állítás lényegében az, hogy a beírt körök átmennek ennek a nagy körnek a középpontján, vagy ha úgy jobban tetszik, a csutka középpontján. Ebből ugyanis már következik, hogy abban a pontban érintik egymást, hiszen ha lenne még egy metszéspontja a beírt köröknek, akkor a csutka hosszetengelyére vonatkozó szimmetria miatt harmadiknak is lennie kellene, de két eltérő körvonalnak legfeljebb két közös pontja lehet.
Alapvetően kétféle módon lehet belátni, hogy a beírt körök átmennek a középponton. Vagy követve a kérdés logikáját, kiindulunk a beírt körökből, és kihasználva azok tulajdonságait, belátjuk, hogy a sugaruk épp fele a nagy kör sugarának, tehát épp a középponton mennek át. Vagy inverz logikát használunk, és vizsgáljuk azt a kört, aminek szimmetria tengelye a csutka hossztengelye, érinti az almacsutka egyik domború oldalát és átmegy a nagy kör középpontján, majd belátjuk erről a körről, hogy ez éppen a beírt kör, azaz érinti a homorú negyedköríveket is.
Sokan keverték a két gondolatmenetet, vagy az inverz gondolatmenetet követték, anélkül, hogy azt kimondták volna. Ennek nyilván az volt az oka, hogy sokan az illusztrációként megadott ábrát használták a számításaikhoz, amin a bizonyítandó már eleve teljesült. Ilyen esetben mindig célszerű dirket eltorzítani kicsit a rajzot, nehogy valami olyasmit használjunk fel automatikusan, amit a rajz sugall, de valójában nem bizonyítottuk. Éppen ezért az alábbi rajzon a beírt kört úgy rajzoltam be, hogy ne menjen át az O középponton. Ebben az esetben a bizonyítandó az, hogy X = O, vagyis az, hogy a beírt kör átmérője megegyezik a nagy kör sugarával: AX = AO.
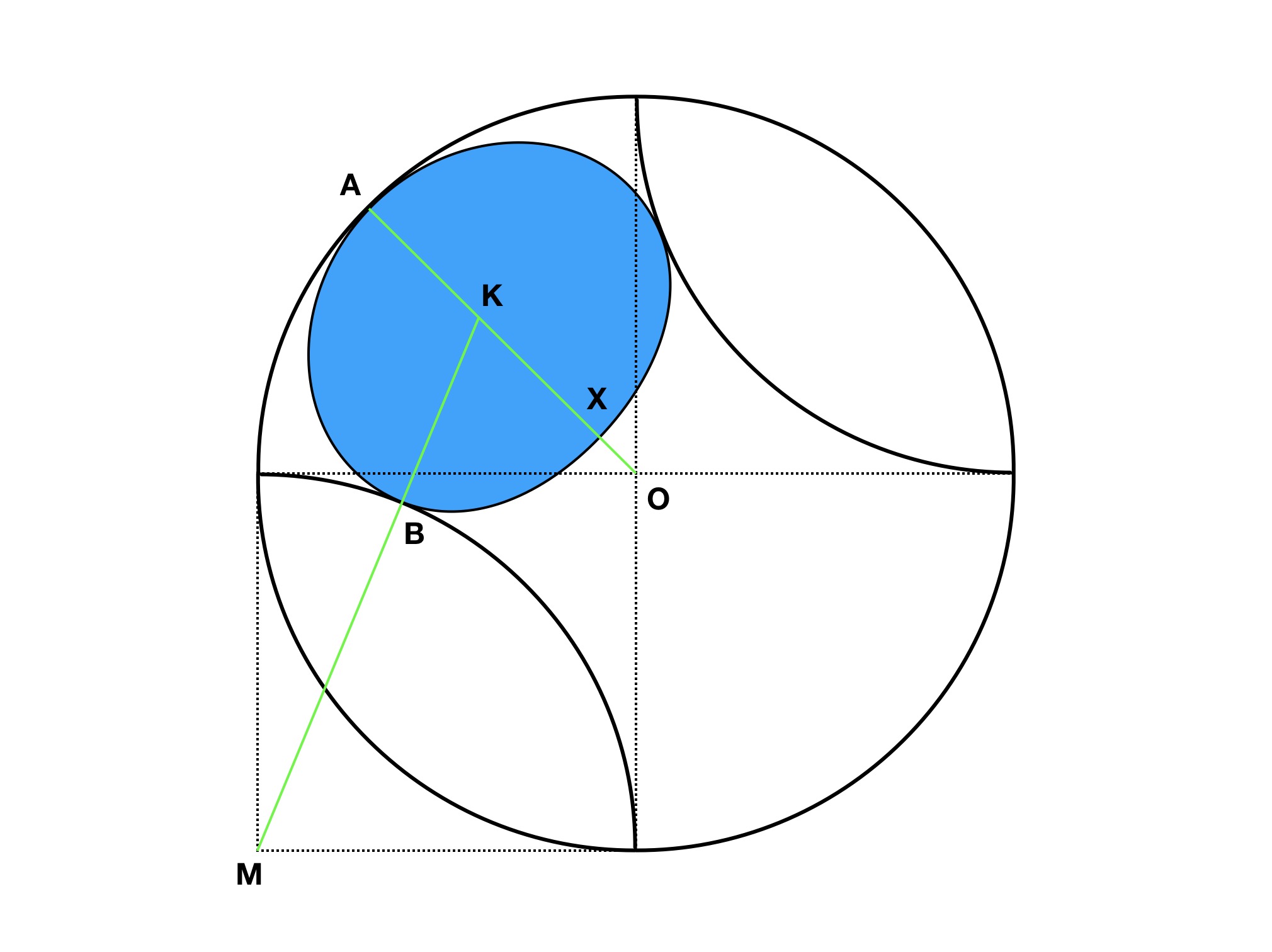
Hogyan tudjuk kiszámolni a beírt kör sugarát, vagyis az AK szakasz hosszát? Vegyük az MOK háromszöget. Mivel MO és OK is 45 fokos szöget zár be a függőlegessel, ezért MOK egy derékszögű háromszög, amire felírhatjuk a Pitagorasz-tételt. Ha a nagy kör sugarát, azaz OA vagy MB hosszát vesszük egységnyinek, és a beírt kör sugarát r-nek nevezzük, akkor a Pitagorasz-tételt így írhatjuk: 2 + (1-r)·(1-r) = (1+r)·(1+r), amiből r = 1/2 adódik, tehát kész is vagyunk.
Hogyan lehet mindezt akár számítások nélkül?
Vígh Máté olvasónk küldött egy gyönyörű megoldást, ami felhasznál egy érdekes geometriai fogalmat és tulajdonságait, aminek a segítségével számolás nélkül is bizonyíthatjuk, hogy a beírt kör átmegy az almacsutka köré írt kör középpontján. Ez a fogalom az inverzió, ami gyakran előkerül, ha körökről van szó, és sok esetben leegyszerűsít érintkező körökkel kapcsolatos feladatokat. Ez nem véletlen, az inverzió másik neve ugyanis körre való tükrözés, így nem csoda, hogy ez a transzformáció körökkel kapcsolatosan hasznos lehet.
Mielőtt ismertetnénk az inverzión alapuló megoldást, pár szót ejtenünk kell az inverzióról és tulajdonságairól. Az inverziónak mindig van egy alapköre, amire tükrözünk. Legyen ezen alapkör középpontja O. Az inverzió olyan transzformáció, ami a sík minden pontjához (O-t kivéve) egy másik pontot rendel. A kör belsejét a körön kívüli tartományba transzformálja, úgymond tükrözi. Ezt úgy teszi, hogy egy adott P pont képe az az P' pont, ami az OP félegyenesen van, és a középponttól mért távolsága R·R/|OP|, ahol R az inverzió alapkörének sugara, |OP| pedig a P pont O-tól vett távolsága. Ha az inverzió alapkörének sugara egységnyi, akkor a közzéppontól |OP| távolságra lévő pont 1/|OP| távolságra kerül.
Az alábbi színes ábra mutatja, hogy az egyes pontok képe hol helyezkedik el. Nem tudom, mennyire jól szemlélteti az inverziót, mindenesetre szép, és tökéletesen leírja a transzformációt, mert az egész síkot kiszíneztük úgy, hogy pont és képe azonos színű. Az inverzió középpontja fehér, ez az egyetlen pont, aminek nincs párja, mert ennek a képe a végtelenben lenne.

Az inverziónak számos érdekes tulajdonsága van. Például kört körbe képez, esetleg elfajult körbe, azaz egyenesbe. Az az ábra alapján is világos, hogy az inverzió körével koncentrikus kört koncentrikus körbe képez, de a síkon lévő tetszőleges kört is körbe képez, még az inverzió alapkörét metsző kört is. Ezen kívül az inverzió szögtartó is, ebből pedig rögtön következik, hogy az inverzió körét merőlegesen metsző köröket önmagukba képezi le. Ennél többre nem is lesz szükségünk.
Az almacsutka domború körívei ugyanazon körön fekszenek, ahogy azt már korábban is megállapítottuk. Ez a fekete kör az alábbi ábrán. Tekintsük az almacsutkába írt kék kör, illetve a homorú narancs és piros negyedkörívek inverzét a fekete körre vonatkozóan. Mivel a homorú és domború negyedkörívek derékszögben találkoznak, az inverzió tulajdonságai miatt a homorú negyedkörívek képei ezen köríveket tartalmazó körök külső részei lesznek, amiket pöttyözött ívekkel jelöltünk ugyanolyan színnel. A kék kör képe egy olyan kör vagy egyenes kell legyen, ami érinti a domború és homorú negyedkörívek képeit, azaz a három nagy kört egyszerre, ami csak úgy lehetséges, ha a kék kör képe a pöttyözött kék egyenes. Az egyenes viszont kimegy a végtelenbe, ezért a kék körnek muszáj átmennie az iverzió fekete körének középpontján, és éppen ez az, amit bizonyítani akartunk.
