A 2019-es nemzetközi π-nap alkalmából az volt a kérdésünk, hogy elő tudjátok-e állítani a 2019-es számot csupán négy π és néhány műveleti jel felhasználásával. A megengedett műveletek az összeadás, kivonás, szorzás, osztás, gyökvonás, hatványozás és egészrész-képzés voltak.

A feladványra több megoldás is érkezett, íme néhány ezek közül, ahol a hatványozást ^ jel, a gyökvonást az sqrt( ) függvény, az (alsó)egészrész-képzést pedig a [ ], azaz kapcsos zárójelek jelölik.

[[π]^sqrt(sqrt(sqrt([π]))·(π^π))]

[[π]^(sqrt(sqrt(sqrt([π])))·(sqrt(π)^π))]

[([π]^(sqrt(π)^π))^sqrt(sqrt(sqrt([π])))]

[[π]^([π]^sqrt(sqrt(π)+sqrt(sqrt(π))))]

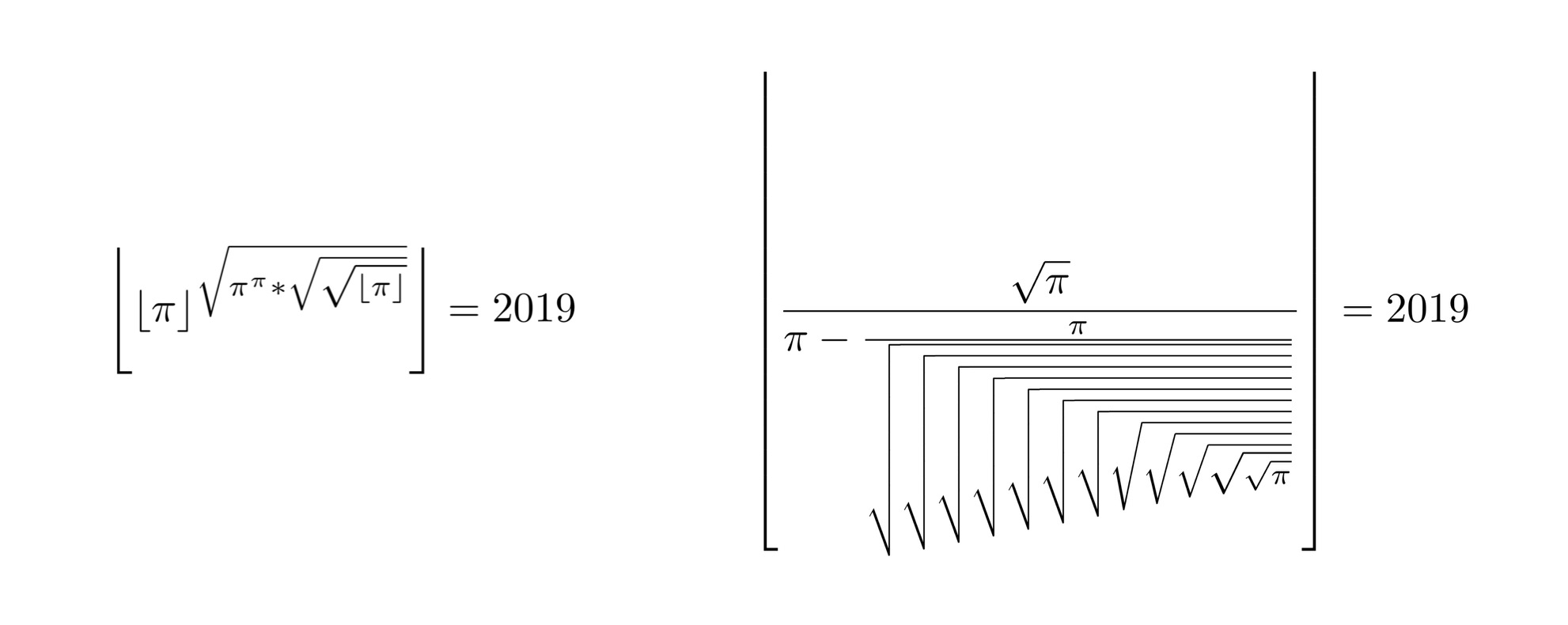
Ezeken kívül még rengeteg van, de ezek a lehető legkevesebb műveletet használják. Boros Péter megoldónk küldött olyan megoldást például, ami csak egyetlen helyen használ egészrész-képzést, viszont 13 gyökvonás is szerepel benne, lásd a jobb oldali képletet fent. Ahhoz hogy ezt helytakarékosan leírjuk, vezessük be az f(k) = π^(1/2^k) jelölést. f(12) tehát azt a számot jelöli, amit úgy kapunk, hogy π-ből 12-szer gyököt vonunk. Ennek a leírásához, ahogy tetszőleges f(k) leírásához elég egyetlen π jelet felhasználnunk a rendelkezésre álló négyből. Ezzel a jelöléssel a csupán egy egészrész-képzést használó megoldás a következő alakban írható: [sqrt(π)/(π -(π/f(12)))]. És ugyancsak ezzel a jelöléssel egy másik megoldás J3L 2404 álnevű megoldónktól: [(f(9)-f(15))/(f(20)-f(30))], ami tehát konceptuálisan egyszerű, de összesen 74 gyökvonást használ.

Ezen a vonalon haladva egyébként a haladó kérdésre is válaszolhatunk. A [π/(f(k)-f(k+1))] például egy olyan sorozat, ahol a nevező zérushoz tart, ahogy k egyre nagyobb egész értékeket vesz föl, tehát végeredményben ennek a végtelen sorozatnak a tagjai egyre nagyobb egész számok lesznek, amik mind előállíthatók három π felhasználásával.

Az eredeti feladat más módon is általánosítható. Ugyancsak Boros Péter mutatta meg, hogy 2019 nem csak négy π-vel, de négy e-vel, az ún. Euler-féle számmal is felírható, lásd alább.

2019 = [sqrt(sqrt(e))·[[e^e]^e]]

Továbbá Boros Péter nem csak a 2019-et, de 1-től 2019-ig minden egész számot előállított négy π felhasználásával, sőt megmutatta, hogy 1-től 100-ig három π is elegendő, de még a 2019 felírásához is elég három, ha elég sok műveletet bevetünk, neki 59 művelettel sikerült megoldania. 2019-et egyébként rövidebben is fel lehet írni három π-vel, ha a műveleti jeleket kicsit kibővítjük és megengedjük a faktoriális képzést, ráadásul nem csak egész számokra. Egy ilyen megoldás Kőfalvi Anna megoldónktól származik, ahol Γ az ún. gamma-függvényt jelöli, amivel a faktoriális képzés még komplex számokra is kiterjeszthető.

[[π!]!-π^[π!]] = [Γ([Γ(π+1)]+1)-π^[Γ(π+1)]]

Mindezek után, ha kezdetben nehéznek is tűnt a feladat és a képleteket látva bonyolultnak tűnhet egy-egy szám felírása, felmerül a sejtés, hogyha akármilyen sok műveleti jelet használhatunk, akkor talán minden egész számot elő lehet állítani négy π vagy akár csupán három π felhasználásával. Éppen ezért különdíjért kitűzöm az alábbi feladatot.

Különdíj a sejtés bizonyításáért vagy cáfolatáért

Aki megmutatja, hogy minden pozitív egész szám előállítható négy π és akárhány a korábbi feladványban megengedett műveleti jel felhasználásával, vagy mutat egy pozitív egész számot, amiről bizonyítani tudja, hogy biztosan nem állhat elő ilyen módon, egy Rubik-gömb a jutalma.

Aki megmutatja, hogy minden pozitív egész szám előállítható három π és akárhány a korábbi feladványban megengedett műveleti jel felhasználásával, vagy mutat egy pozitív egész számot, amiről bizonyítani tudja, hogy biztosan nem állhat elő ilyen módon, egy Planet - Egy éledő világ a tenyeredben! nevű társasjáték a jutalma.

Beküldési határidő: végtelen. A díjat az első helyes megoldó kapja!

Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus és bűvész