Ész Ventura: Hogyan képzeljünk el öt hiperkockát négy dimenzióban?

4D pentakockák című feladványunkban az volt a kérdés, hogy öt darab négydimenziós egységkockából, amikre ezentúl a hiperkocka elnevezést fogjuk használni, hány különböző, úgynevezett négydimenziós pentakocka, azaz a fenti elnevezést használva, pentahiperkocka építhető?

A négy dimenziótól nem kell megijedni, hamarosan rátérünk arra, hogyan érdemes elképzelnünk a négy dimenziót és a hiperkockákat, de előtte tisztázzunk még két alapvető fogalmat. Az egyik az egybevágóság, a másik a merev testek folytonos mozgása.

Két geometriai alakzat akkor egybevágó, ha távolságtartó transzformációval egyik a másikra képezhető. Ilyen távolságtartó transzformációk tetszőleges dimenzióban az eltolások, forgatások és tükrözések. Ezek a transzformációk matematikai konstrukciók, azonban az eltolás és a forgatás merev testeken fizikailag is megvalósítható folytonos mozgásként, ellentétben a tükrözéssel. Mindenki tudja, hogy egy balkezes kesztyűt akárhogy is mozgatunk, nem tudunk fedésbe hozni egy jobbkezes kesztyűvel, hacsak nem fordítjuk ki, de akkor már nem marad merev.

Megállapíthatjuk tehát, hogy akkor, ha két alakzat vagy merev test egymásba mozgatható, akkor egybevágóak, de ha egybevágóak, még nem biztos, hogy egymásba is mozgathatók. Továbbá ha egy test nem tükrösen szimmetrikus, akkor kétféle formában fordulhat elő, ahogy a kesztyűből is van bal- és jobbkezes verzió. Mindezek a megállapítások tetszőleges dimenzióban érvényesek.

De hogyan képzeljük el a kockát?

Mármost nézzük, hogyan képzeljünk el egy négydimenziós hiperkockát. Ehhez előbb vizsgáljuk meg kicsit, hogyan épülnek fel az alacsonyabb dimenziós kockák, azaz a kétdimenziós négyzet és a háromdimenziós kocka. Egy tetszőleges dimenziós kocka olyan konvex szabályos test, amelynek élei egyforma hosszúak, és bármely két éle vagy párhuzamos vagy merőleges egymásra.

Az egydimenziós ,,kocka'' a szakasz. A szakasz egy egydimenziós egyenesen fekszik. Ebből négyzetet úgy kapunk, hogy kilépünk az egy dimenzióból, és a szakaszt az eredeti egyenesre merőlegesen eltoljuk egy második dimenzió irányába, mégpedig pont az eredeti szakasz hosszával, majd az eredeti szakasznak és az eltolt szakasznak a megfelelő csúcsait egyenes szakaszokkal összekötjük. A négyzetet tehát négy szakasz fogja határolni, amik merőlegesek egymásra.

Ha a négyzetet toljuk el a bennfoglaló síkjára merőlegesen egy oldalhossznyival egy harmadik dimenzió irányába, majd az eltolt négyzet csúcsait összekötjük az eredeti négyzet megfelelő csúcsaival, akkor kapjuk a kockát. A kockának tehát kétszer annyi csúcsa lesz mint a négyzetnek volt, éleinek száma 4 + 4 + 4 = 12, és hat négyzet fogja határolni.

Gyártsunk hiperkockát!

Ahhoz, hogy a hiperkockát megkapjuk, ugyanezt kell tennünk: eltolunk egy kockát a negyedik dimenzió irányába, majd összekötögetjük a megfelelő csúcsokat. Ezt nehéz elképzelnünk, mert a világot, amiben élünk, háromdimenziósnak érzékeljük, de azért illusztrálhatjuk, még akár egy kétdimenziós papíron is. Kockát tudunk rajzolni papírra, például perspektivikusan. Rajzoljunk két kockát, például egyiket a másikba, ahogy az alábbi illusztráció bal oldali ábráján is látszik, majd kössük össze rendre a csúcsaikat. A két kockát úgy kell elképzelnünk, mint ha más térben lennének, egymással párhuzamos terekben, mondhatnám azt is, hogy hiperrétegekben. Akár másik papírra is rajzolhattuk volna, de mi most egy papírt használunk, csak tartsuk számon, hogy a belső kocka másik réteg. Ugyanígy különböző rétegeket reprezentálunk egyébként egyazon síkon, amikor egy háromdimenziós kockát rajzolunk a papírra.

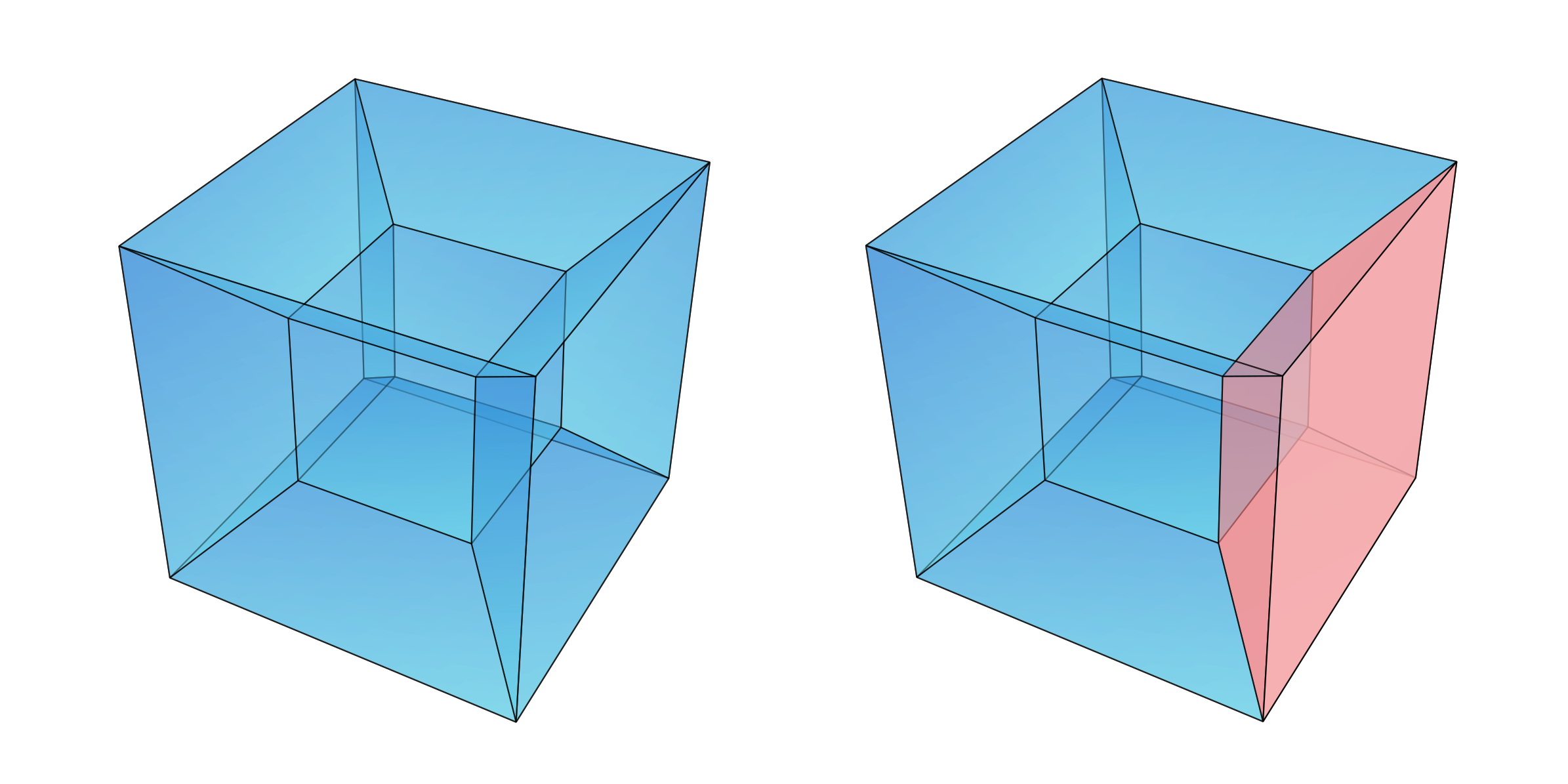
A hiperkocka csúcsainak száma kétszerese a kockáénak, vagyis 16. Az éleinek számát az illusztráció alapján leszámolhatjuk: 12 + 12 + 8 = 32. Határoló oldalai pedig háromdimenziós kockák, szám szerint nyolc, ezekből színeztünk be egyet pirosra a jobb oldali ábrán. Ilyen csonka piramissal illusztrált kockából láthatunk még hatot, és van még a belső kis kocka és a külső nagy kocka. Fontos, hogy ezek a kockák elvileg ugyanakkorák, teljesen egybevágóak a négydimenziós térben, csak ebben az ábrázolásban torzak, mert csak így oldható meg ebben a ,,hiperperspektivikus" ábrázolásban.

Talán még szemléletesebb úgy elképzelni, hogy van egy könyved, aminek minden lapja a négydimenziós tér egymással párhuzamos háromdimenziós (hiper)rétegeit reprezentálja. Az egyes lapokon pedig a szokásos perspektivikus ábrázolással rajzoljuk le azt, hogy mit látunk az egyes rétegekben. Ha így képzeljük el, akkor a hiperkocka nem lesz más, mint egy könyv, aminek minden oldalán egy ugyanolyan kockát láthatunk. Azok az élei a hiperkockának, amiket az összekötögetés során húztunk be korábban, ebben a könyvben a lapokat függőlegesen keresztüldöfő a könyv igazi bennfoglaló terében haladó lapokra merőleges egyenesek lennének.

Na de el kell nekünk egyáltalán képzelnünk a hiperkockákat ahhoz, hogy választ adjunk a feladat kérdésére? Nem igazán. Elegendő, ha koordinátákkal reprezentáljuk a pentakockát felépítő egység hiperkockák pozícióit. Egyszerű dolgunk van, mert a pentakockák egy hiperkockarácsra illeszkednek, ezért dolgozhatunk csak egész értékű koordinátákkal. A kétdimenziós négyzetrácson például az L alakú pentominó megfelelő koordinátarendszer választás után megadható az alábbi középpontú egységnégyzetekkel: (0|0), (1|0), (1|0), (2|0), (3|0). A hiperpentakockákat ugyanígy adhatjuk meg, csak kettő helyett négy koordináta ad meg minden hiperkocka középpontot (x|y|z|q) alakban.

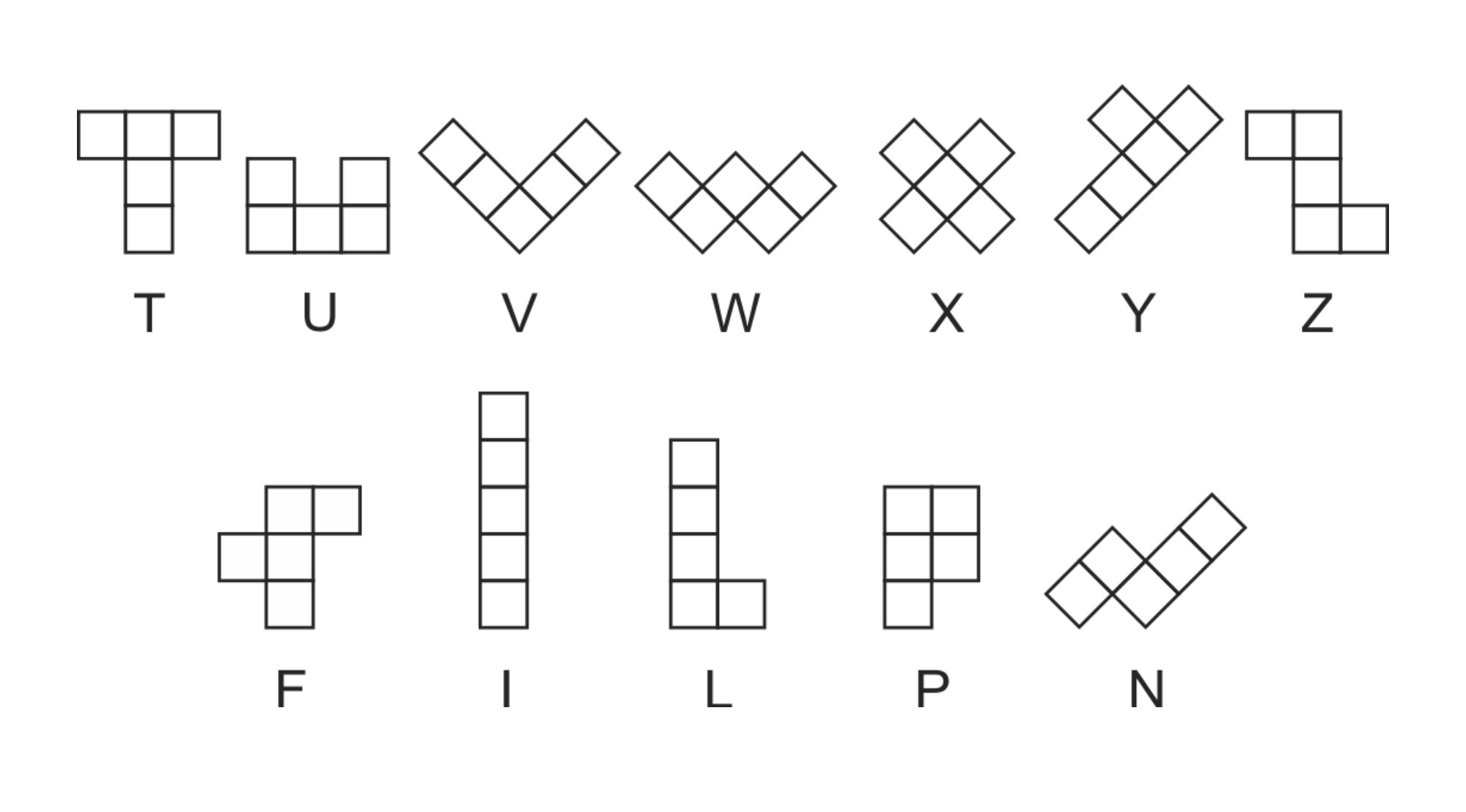
Még mielőtt azonban a valódi négydimenziós pentakockákra rátérnénk, amelyeknek a négydimenziós tér minden irányába van több egységkockányi kiterjedésük, azelőtt számoljuk le azokat a 4D pentakockákat, amik a síkbeli pentominók és térbeli pentakockák megfelelői a négydimenziós térben. A síkbeli pentominók száma 12, amint azt a fenti ábra is mutatja, és ez a feladatban is meg volt adva segítségként. 

Hasonlóan meg voltak adva a térbeli pentakockák is, ezekből 17 darab van, viszont ezek között vannak olyanok tükörképpárok, amik egybevágóak egymással. Ilyen tükörképek az alábbi hat pár: d-e, f-g, h-i, j-k, l-m, n-o. Ezek a háromdimenziós téren belül nem forgathatók egymásba, de a négydimenziós térbe kilépve már igen. Négy dimenzióban tehát a 17 térbeli pentakockából csak 17 - 6 = 11 különböző marad.

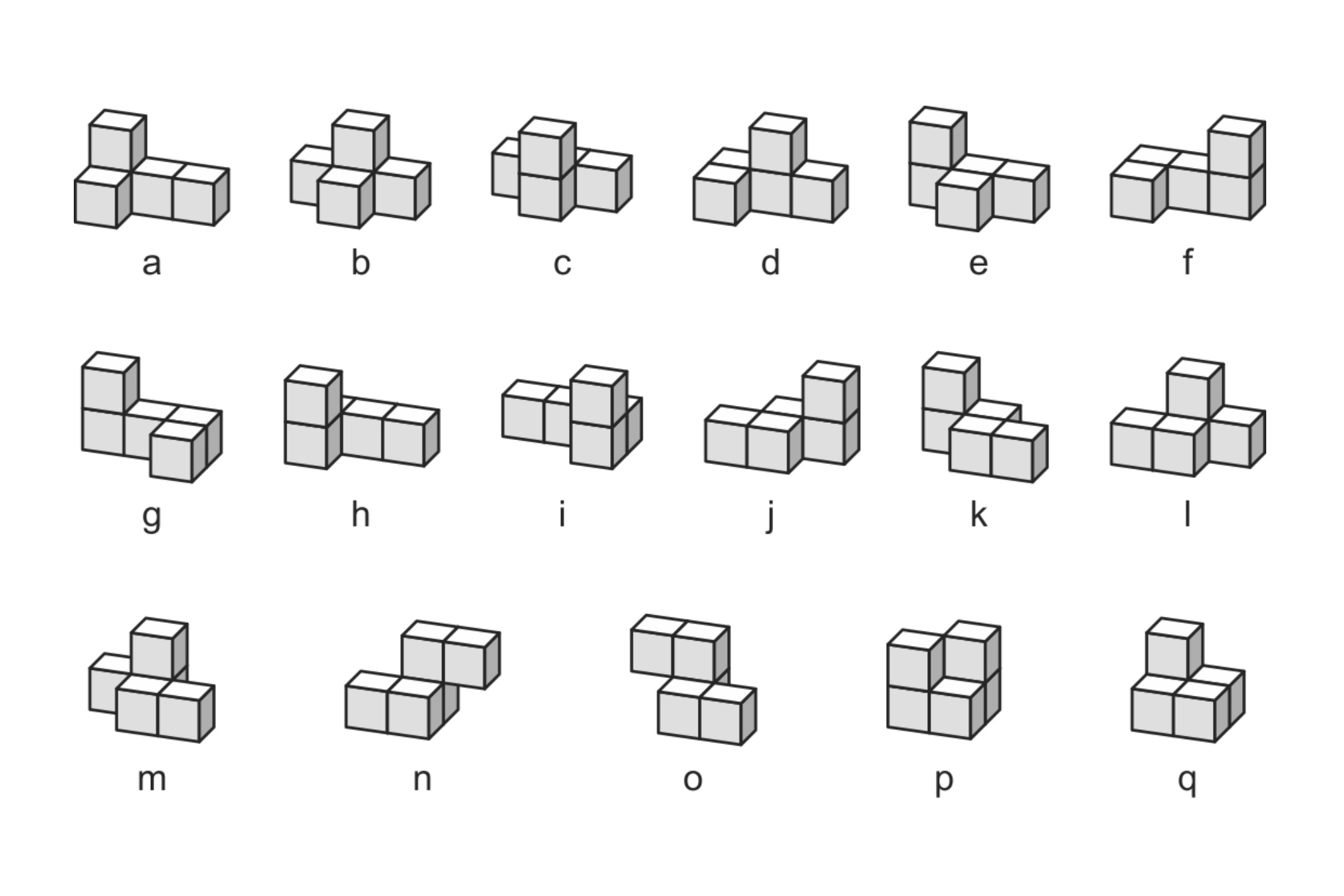
A fenti pentominók és pentakockák négydimenziós megfelelőit természetesen nem teljesen úgy kell elképzelnünk, mint ahogy a fenti ábrákon látszanak, hanem hasonló elrendezésben kell egymás mellé pakolnunk hiperkockákat. Mivel azonban ezek a speciális 4D pentakockák a négydimenziós hiperkockarácsnak csak egy térbeli vagy síkbeli rétegében fekszenek, ez azt jelenti, hogy az alkotó hiperkockáik egyik koordinátája konstans, illetve a hiperpentominók esetében kettő is, és ha ezeket a koordinátákat elhagynánk, akkor a koordinátareprezentációjuk pontosan megegyezne a fenti pentominók és pentakockák reprezentációival az alacsonyabb dimenziós terekben.

Hány ilyen kocka van?

Láttuk tehát, hogy van 12 + 11 = 23 olyan négydimenziós pentakocka, amelyek nem terjeszkednek a négy dimenzió minden irányába. Már csak az a kérdés, hogy hány olyan, van amelyek kiterjedése minden irányba legalább két rétegnyi, azaz valódi négydimenziós objektumok.

Ehhez nézzük meg, hogy hány kocka kell egyáltalán ahhoz, hogy minden irányba terjeszkedjünk. Síkban ehhez három négyzet kellett, mert, ha lerakunk egy négyzetet, akkor annak két szomszédos oldalához kell rakni legalább egy-egy négyzetet, hogy ne csak sorban legyenek. Térben legalább négy kocka kell, vagyis egy kockához legalább három másikat kell illeszteni a tér három irányába, hogy ne csupán egyrétegű alakzatunk legyen. Általában N dimenzióban minimálisan N+1 hiperkockára van szükség, hogy az alakzatunk az N dimenzió minden irányába terjeszkedjen. Ez azt jelenti, hogy négy dimenzióban pont fel kell használjuk mind az öt hiperkockánkat, hogy létrehozzunk egy ilyen alakzatot, tehát viszonylag kevés variációt kell végignéznünk.

Kezdjük tehát egyesével letenni az egység hiperkockákat, és tartsuk szem előtt, hogy minden egyes új hiperkocka letételével egy új dimenzió mentén kell terjeszkednünk. Az első hiperkocka középpontjának koordinátája az általánosság megszorítása nélkül legyen a (0|0|0|0) pont. A második hiperkockának ezzel szomszédosnak kell lennie, de hogy melyik oldal mentén, az lényegtelen, mert egyelőre egyik oldal sem kitüntetett, ezért továbbra is az általánosság megszorítása nélkül feltehetjük, hogy a következő hiperkockának a középpontja az (1|0|0|0) pont. Az elrendezéseket az alábbi ábra szemlélteti, ahol a kék kocka az első hiperkockának, a narancs kocka a második hiperkockának felel meg, csak itt most lehagytuk a negyedik (egyébként konstans nulla) koordinátákat, hogy háromdimenziós kockákkal tudjunk szemléltetni.

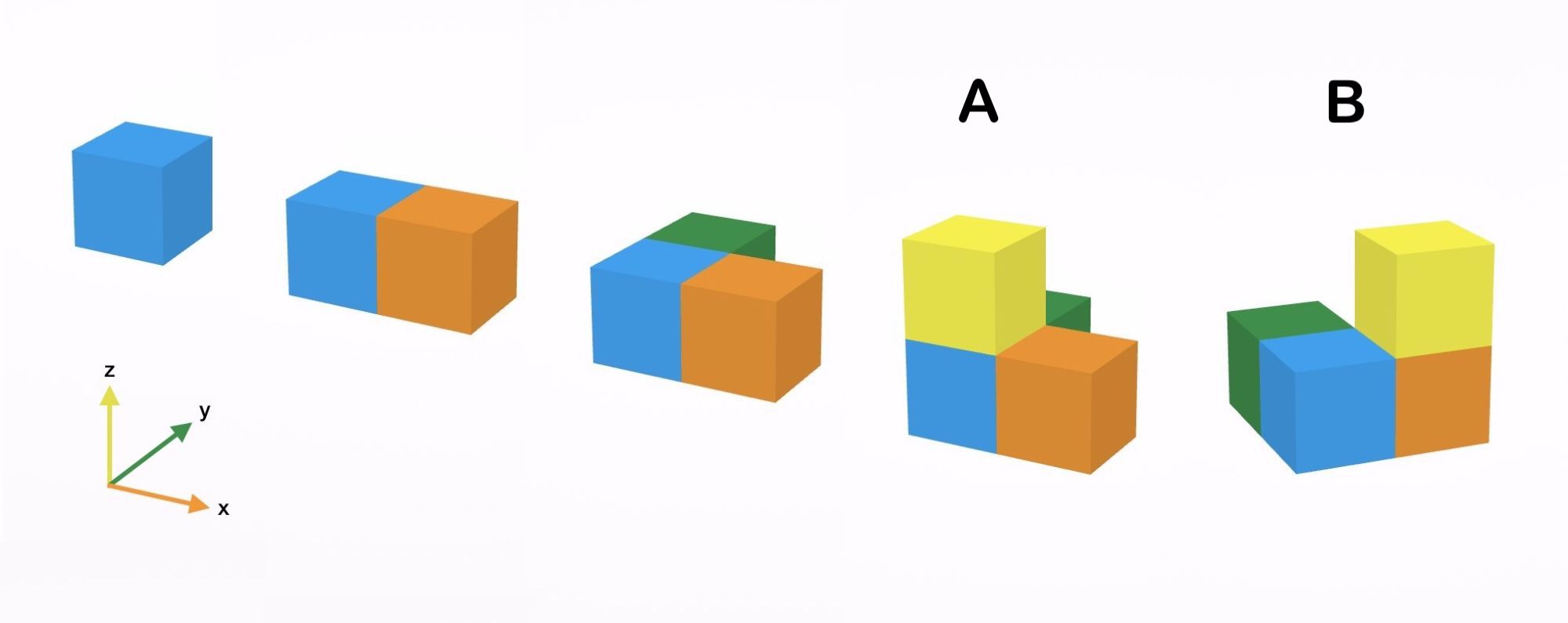
Mivel a két hiperkockából álló alakzatban a két hiperkockának a szerepe teljesen szimmetrikus, azért amikor a harmadik hiperkockát szeretnénk az előző kettőhöz hozzáilleszteni úgy, hogy ne essenek a hiperkockák egy sorba, akkor megint csak az általánosság megszorítása nélkül feltehetjük, hogy a harmadik hiperkocka középpontja a (0|1|0|0) pont. Ennek a hiperkockának a háromdimenziós vetületét sötétzölddel illusztráltuk a fenti ábrán.

Amikor azonban a negyedik hiperkockát illesztenénk az előző háromhoz, akkor már két különböző lehetőségünk is van.  A három hiperkockából álló L-alakzatban ugyanis már nem egyforma szerepet tölt be az összes alkotórész, hiszen a L szögletében álló kék kockának például két szomszédja is van, míg a L végpontjaiban álló narancs és zöld kockáknak csak egy szomszédjuk. Amikor tehát a negyedik sárgával jelölt kockát hozzáillesztjük az előzőekhez, akkor választhatunk, hogy az L szögletében álló kékhez vagy valamelyik másikhoz illesztjük. Ezeket illusztrálja az az A és B alakzat a fenti ábrán, és bár a B-nek a tükörképe is szóba jöhetne, de négy dimenzióban a háromdimenziós tükörképek egymásba forgathatók.

A kérdés tehát az, hogy az ötödik hiperkockát hányféle módon illeszthetjük úgy az előző két alakzat valamelyikéhez, hogy lényegileg különböző valódi négydimenziós pentakockákat kapjunk. Az A alakzat esetében illeszthetünk a kékhez, vagy valamelyik másikhoz, például a narancshoz. Az ugyanis mindegy, hogy a zöldet, sárgát, vagy narancsot választjuk, hiszen egymásba átforgathatók. Bármelyikhez illesztünk, a negyedik koordináta nem lehet zérus, mert ki kell lépnünk a térből. És két lehetőségünk van, vagy +1 vagy -1 a negyedik koordináta.

A B alakzat esetében szintén két lényegileg különböző lehetőség van a tekintetben, hogy melyik kockához illesztünk, mondjuk a kék és a zöld. És ezeken belül is két lehetőség van, amikor a negyedik koordináta +1 vagy -1. Összesen tehát nyolc lehetséges eset van, a kérdés csak az, hogy ezek közül melyek lesznek különbözőek, amik nem forgathatók egymásba.

A nyolc eset az alábbi:

(0|0|0|0), (1|0|0|0), (0|1|0|0), (0|0|1|0), (0|0|0|1)
(0|0|0|0), (1|0|0|0), (0|1|0|0), (0|0|1|0), (0|0|0|-1)
(0|0|0|0), (1|0|0|0), (0|1|0|0), (0|0|1|0), (1|0|0|1)
(0|0|0|0), (1|0|0|0), (0|1|0|0), (0|0|1|0), (1|0|0|-1)
(0|0|0|0), (1|0|0|0), (0|1|0|0), (1|0|1|0), (0|0|0|1)
(0|0|0|0), (1|0|0|0), (0|1|0|0), (1|0|1|0), (0|0|0|-1)
(0|0|0|0), (1|0|0|0), (0|1|0|0), (1|0|1|0), (0|1|0|1)
(0|0|0|0), (1|0|0|0), (0|1|0|0), (1|0|1|0), (0|1|0|-1)

Mivel derékszögű rácson dolgozunk, lényegében 90 fokos forgatásokkal minden szóba jövő forgatás előállítható az esetünkben. A kérdés tehát az, hogy ilyen 90 fokos forgatásokkal és esetleg eltolásokkal melyek transzformálhatók egymásba. A 90 fokos forgatás tetszőleges dimenzióban pedig úgy írható le a koordináták nyelvén, hogy kiválasztunk két koordinátát, felcseréljük őket, és az egyik elé egy mínusz előjelet írunk. A többi koordinátát mindig változatlanul hagyjuk, ez felel meg annak, hogy térben egyenes körül forgatunk tehát ott van egy fix koordináta, négy dimenzióban pedig sík körül forgatunk, azaz két koordináta marad fixen.

Az 1. és a 2. eset például ugyanaz, hiszen az utolsó két koordinátát választva cserére áttranszformálhatók egymásba. Hogy melyek még az ekvivalensek, azokat a kedves olvasóra bízom. Végeredményben kiderül, hogy összesen csak négy különböző marad. Így tehát a legvégső eredmény, hogy összesen 12 + 11 + 4 = 27 négydimenziós pentakocka létezik. Ez ellenőrizhető a számsorozatok online enciklopédiájában (OEIS) is.

Érdekes, hogy a háromdimenziós pentakockák száma 12 + 17 = 29, vagyis három dimenzióig nő a pentakockák száma, de négy dimenzióban már kevesebb van, mint három dimenzióban. Öt dimenzióban pedig még egyel kevesebb lenne, mert az egyik négydimenziós pentakocka nem tükörszimmetrikus, tehát négy dimenzióban még párban szerepel, de öt dimenzióban ezek már egymásba forgathatók.