Ész Ventura: A vízminőség-ellenőr úgy megy, akár a fény

Az 59. Ész Ventura feladványban a vízminőség-ellenőrnek úgy kellett az A városból a tőle 11 kilométerre fekvő B városba mennie (fekete pontok), hogy közben a tóból és a folyóból is mintát vegyen. A legrövidebb út volt a kérdés.

Tegyük fel, hogy az ellenőr az A pontból indulva először elmegy a tóhoz mintát venni. Jelöljük F-fel a tó kerületének azt a pontját, ahol a mintát veszi. Innen elmegy a folyóhoz mintát venni, a második mintavétel helyét jelöljük D-vel. Nyilvánvaló, hogy A és F között, F és D között, és D és B között egyenesen halad, hiszen két pont között a legrövidebb út az egyenes, ha nincs közben akadály. Ha az ellenőr először a folyóból venne mintát és aztán a tóból, akkor a városok átnevezésével vissza tudnánk vezetni a feladatot a fenti esetre, elég tehát csak ezt tekinteni.

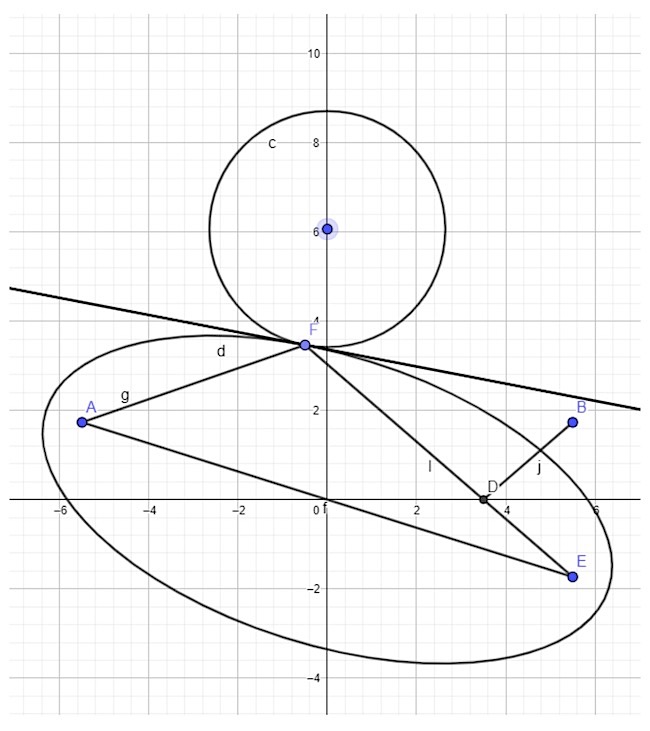
Tükrözzük a B pontot a folyó vonalára, így kapjuk az E pontot. Mivel a DB szakasz hossza a tükrözés miatt megegyezik a DE szakasz hosszával, a feladat arra redukálódik, hogy az AFE távolságot minimalizáljuk, vagyis az AF és FE szakaszok hosszának összegét.

Ha veszünk egy A és E fókuszpontú ellipszist, akkor az ellipszis kerületének bármely G pontjára az AGE útvonal hossza ugyanakkora lesz. Minél nagyobb az ellipszis, annál nagyobb az út hossza, nekünk viszont a legrövidebb út kellene, csakhogy a tavat is érinteni kell. A keresett F pont tehát éppen a kört érintő ellipszisnek az érintési pontja lesz, ahogy az Ureczky József megoldónk fenti ábráján látszik.

Másképp is lehet gondolkodni. Az optikában az úgynevezett Fermat-elv azt mondja ki, hogy egy fénysugár mindig olyan pályát követ, hogy a terjedési idő a lehető legkisebb értéket vegye fel. Ha olyan közegek vannak, amiben a fény terjedési sebessége eltérő, vagyis eltérő a törésmutató, akkor ebből az elvből levezethető például a Snellius–Descartes-féle fénytörési törvény. Változatlan fénysebesség mellett pedig a tükrökről való fényvisszaverődés törvénye is megmagyarázható, ami azt mondja ki, hogy a beesési és visszaverődési szögek azonosak.

Hogyan jön ide az optika? Hát úgy, hogy ha azonos sebességgel halad a vízminőség-ellenőr, akkor a legrövidebb út és a legrövidebb idejű út megtalálása egymással ekvivalens. A Fermat-elv alapján pedig a feladat analóg lesz azzal, hogy milyen úton jut el a fény A pontból a B pontba, ha a tó kerületét és a folyó partját tükröző felületnek tekintjük. Lényegében az a kérdés, hogy az A pontban álló ember a kör alakú tükör melyik F pontjába kell nézzen, hogy ott a B pont kétszeresen visszavert tükörképét lássa.

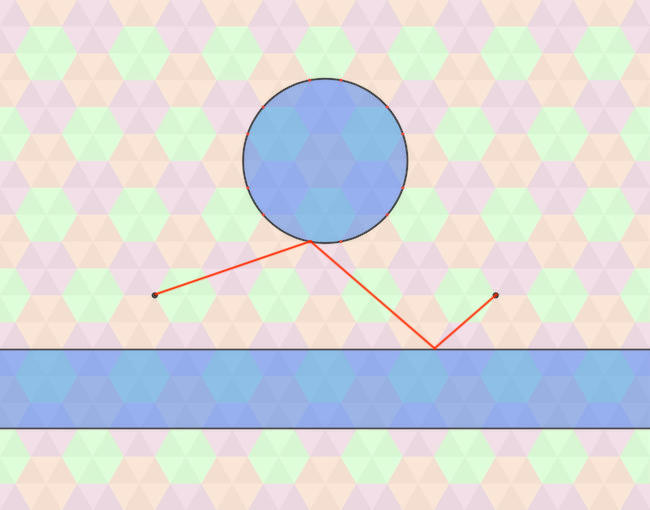
A megoldás a korábban említett ellipszis érintkezési pontja, azonban az optikából vett analógia alapján tudjuk azt is, hogy a fenti ábrán a piros vonallal jelölt pálya beesési és visszaverődési szögeinek a tükröződési pontokban, azaz a töréspontokban azonosaknak kell lenniük. A feladatban szereplő speciális esetben szerencsénk van, mert az F pont éppen egy rácspontra fog esni, a fenti ábra alapján ugyanis könnyen ellenőrizhető, hogy a pirossal jelölt útvonal a megoldás, ami mindkét töréspontban teljesíti a beesési és visszaverődési szögek egyenlőségének feltételét. A kör kerületén lévő F törési pontnál a kör középpontjából az F pontba menő sugár az, amihez viszonyítva a beesési és visszaverődési szöget mérnünk kell.

Mivel a térképen egy kis háromszög oldala egységnyi, ezért könnyen kiszámolható a rácspontok között menő törött vonal hossza, amire 5·√7 ≈ 13,23 km adódik.