Tavaly az idősek világnapja alkalmából egy különleges ötgenerációs családfával kapcsolatban tűztünk ki feladványt. Aki akkor nem oldotta meg, annak javasoljuk, hogy a megoldás elolvasása előtt essen neki ennek a háromkoponyás családi feladatnak.

A feladat a következő volt:

Egy ükszülő minden gyerekének, unokájának és dédunokájának is van már gyereke, de nincs még szépunokája. Összesen több mint 50 ükunokája van, viszont se neki, se senkinek a leszármazottai között nincs háromnál több gyereke. Az az érdekesség figyelhető még meg a családjában, hogy minden gyerekének ugyanannyi leszármazottja van, viszont minden unokájának különböző. Mutassuk meg, hogy az ükszülő minden gyerekének vagy egyforma számú unokája van, vagy mindegyiknek különböző számú unokája van.

Először is megállapíthatjuk, hogy egy unokának legfeljebb 12 leszármazottja lehet: 3 gyereke és 3 × 3 = 9 unokája. Ennyi azonban csak egy unokának lehet, a többinek sorban egyre kevesebb, hiszen a feladat szövege szerint nincs két unoka egyező számú leszármazottal. Mivel az ükszülőnek legfeljebb 9 unokája lehet, ezért az ő leszármazottaiknak a maximális száma rendre 12, 11, 10, 9, 8, 7, 6, 5, 4 lehet. Egy lehetséges realizáció az alábbi ábrán látszik, ahol kékkel van jelölve a 9 unoka és naranccsal az ő gyerekeik (dédunokák) és pirossal az unokáik (ükunokák).

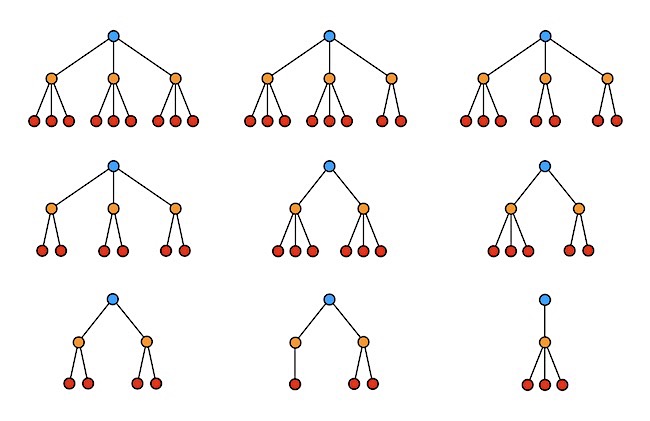
Nézzük meg az egyes esetekben az ükunokák maximális számát az adott ágon. Mivel az unokák leszármazottai dédunokákból és ükunokákból tevődnek össze (narancs és piros pöttyök), ezért az egyes esetekben akkor kapjuk a legtöbb ükunokát (pirosat), ha a dédunokák száma (narancsok) a lehető legkevesebb. 12, 11, 10 és 9 esetén kell legyen legalább három gyereke (három narancs pötty) az unokának, mert két gyerekkel csak 2 + 6 = 8 lenne a leszármazottak maximális száma. 8, 7, 6 és 5 esetén pedig kell legyen legalább két gyereke az unokának, mert egy gyerekkel csak 1 + 3 = 4 lehetne a leszármazottak maximális száma. Mindezeket figyelembe véve az ükunokák maximális száma rendre 9, 8, 7, 6, 6, 5, 4, 3, 3 lehet, ami pedig összesen maximum 51 ükunokát jelent. A feladat szerint viszont legalább 51 ükunoka van, tehát ennél kevesebb nem is lehet. Így tehát az ükszülőnek kell legyen 9 unokája és mindegyiknél maximális kell legyen az ükunokák száma, ahogy az ábrán is látszik egy lehetséges realizáció erre.

Mivel az unokák száma 9, tudjuk azt is, hogy 3 gyereke van az ükszülőnek. Ez alá a három gyerek alá kell most az unokákat úgy hármas (testvéri) csoportokba rendezni, hogy a gyerekek leszármazottainak száma (narancs és piros pöttyök egybevéve) megegyezzen, hiszen ezt írta a feladat. Ezt csak kétféleképpen tehetjük meg:

12 + 8 + 4 = 11 + 7 + 6 = 10 + 9 + 5
12 + 7 + 5 = 11 + 9 + 4 = 10 + 8 + 6

Az első esetben a gyerekek unokáinak (dédunokák) száma rendre 3 + 2 + 1 = 6, 3 + 2 + 2 = 7, 3 + 3 + 2  = 8 (narancs pöttyök), míg a második esetben 3 + 2 + 2 = 7, 3 + 3 + 1 = 7, 3 + 2 + 2 = 7. Az egyik esetben tehát 6, 7, 8, vagyis mind különböző, míg a másik esetben 7, 7, 7, azaz mind egyforma, amit bizonyítani kellett.

Kapcsolódó cikk a Qubiten: