„A semmiből egy új, más világot teremtettem” – írta Bolyai János édesapjának az új, nemeuklideszi geometria megalkotásakor. De teremtés volt ez vagy felfedezés? Egy interjúbeszélgetésben hamarosan visszatérek arra, hogy mit gondolnak erről a kor matematikusai, filozófusai, felfedezői. Ha teremtés volt valóban, akkor viszont a matematika az, ahol az ember a legszabadabban teremthet.

Pintér Gergőnek a Typotex kiadó gondozásában megjelent könyve új világok teremtéséről szól; arról, hogy milyen szabad a matematika. Sokszor valóságos problémák, máskor pedig az emberben szunnyadó örök kíváncsiság vezet oda, hogy kilépjünk egy más térbe, más terekbe, konkrétan és átvitt értelemben is akár más dimenziókba, ahonnan rálátás és új perspektíva nyílik az érdeklődő ember számára, aki ezáltal mélyebb igazságokat és szépséget élhet át.

Gergő könyve ismeretterjesztő könyv, amely az általa sok-sok éve tartott MateMorfózis szeánszok legérdekesebb témáinak közös geometriai szemléletű szálra felfűzött gyűjteménye. A kocsmákban és fesztiválokon tartott MateMorfózis előadások célja a közös beszélgetés, hogy közünk lehessen a körülöttünk lévő, tudománnyal átitatott világhoz – erre Gergő használ egy új kifejezést is: radikális közösségi ismeretterjesztés.

A könyv a MateMorfózis előadásokat idéző párbeszédes formában íródott, kerülve a képleteket, de végigvezetve az olvasót minden a témákkal kapcsolatban szokásosan felmerülő kérdésen, közben közös gondolkodásra sarkallva az olvasót. A könyv nem csak a túlművelt természettudományos érdeklődésű embernek szól, de inspiráló lehet a matematikához fűződő viszonyt tekintve teljesen laikus olvasóknak, akár művészeknek is. Gergőt magát is inspirálták ezek a témák, hiszen több zenekarában (aktuálisan éppen a Kronoszinklasztikus Infundibulum) is előjönnek ezek a gondolatok dalszövegek formájában, amikből a könyvben is találunk néhányat.

Visszatérve Bolyaihoz, miután kiderült, hogy nemcsak egy abszolút geometria létezik, a 19. század elejétől bevett gyakorlat lett új világok teremtése, ami aztán alapjául szolgált a fizikai avantgárdnak is, a relativitáselmélet és kvantummechanika megjelenésének, ami már nem csak a gondolkodásunkat, de környezetünket is teljesen átalakította. Ezeket a hatásokat látjuk, tapasztaljuk, elhisszük, de sokszor komoly matematikai ismeretek kellenek ahhoz, hogy lássuk a hasznát egy-egy olyan fiktív matematikai fogalom bevezetésének, mint mondjuk a görbült tér, a magasabb dimenziók vagy akár csak a komplex számok.

Gergő a geometria területén igyekszik nemcsak szemléletessé tenni fontos fogalmakat, de megmutatni a róluk való gondolkodás hasznát is: ide tartozik például a több dimenzió, a topológia, a végtelen távoli ideális pontok vagy a szimmetriák. Az egyik legérdekesebb fejezet ebből a szempontból, ahol a geometria a leváratlanabb helyen segít, amikor kiderül, hogy a Dobble kártyajáték létezése annak köszönhető, hogy létezik hetedrendű véges projektív sík, és ez önmagában sem magától értetődő. Erről egyébként sok helyen lehet olvasni az interneten is, de ilyen szépen, szemléletesen, részletesen és az olvasót rávezetve sehol nem láttam még.

A témában mindenképpen ajánlom Gergő könyvének megfelelő fejezetét, itt most csak dióhéjban összefoglalom a lényeget, mert ehhez kapcsolódik a mai feladványunk. A Dobble egyébként egy nagyon népszerű gyorsasági játék, Angliában pár év alatt több mint egymillió eladott példánnyal 2018-ra a legnépszerűbb kártyajáték lett. A Dobble fémdobozában 55 kerek lapot találunk. Ezek mindegyikén nyolc szimbólum található, amikre teljesül, hogy bármely két lap szimbólumai között pontosan egy közös szimbólumot találunk – ezt kell gyorsan felismerni.

A Dobble-pakli lényegében egy véges projektív geometriai rendszer reprezentációja. Gondoljunk arra, hogy minden kártya egy pont, és minden szimbólum egy egyenes valamilyen geometriai rendszerben. Ha így tekintünk rá, akkor bármely két pont között megy pontosan egy egyenes (van közös szimbólum). De nézhetjük fordítva is: legyenek a kártyák egyenesek és a szimbólumok pontok – ebben az esetben bármely két egyenesnek kellene legyen közös pontja. Na de álljunk csak meg egy pillanatra: a párhuzamosok sosem metszik egymást. Vagy mégis? A hagyományos síkon nem, de ha bevezetjük a végtelen távoli ideális pontokat, megkapjuk az úgynevezett projektív síkot, ahol már bármely két egyenesnek pontosan egy közös pontja van.

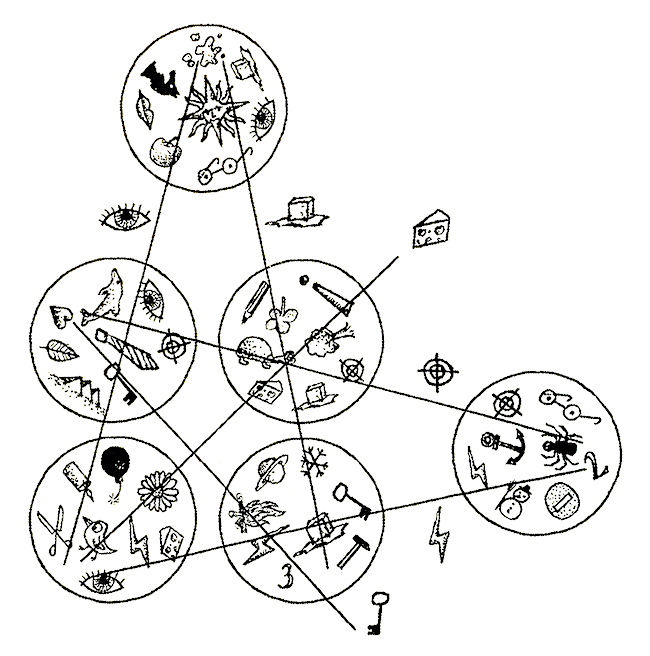
Matematikusok számára a projektív sík nagyon hasznos, a hagyományos geometriát is azon szokták művelni, mert nagyon praktikus például a dualitás miatt: ha bebizonyítasz egy tételt, akkor annak a duálisa is azonnal érvényes, amiben a pontokat és egyeneseket (a szavakat) csak kicseréled egymással, teljesen szimmetrikus a dolog. Projektív síkon a dolgok bezáródnak, az ellipszis, a parabola és a hiperbola ugyanolyan objektum, csak a nézőpont más. És, mint láthatjuk, a projektív sík nemcsak a matematikusoknak, de nekünk is hasznos, mert nélküle nem lenne Dobble.

A projektív síkon persze végtelen sok egyenes és pont van, ezért a Dobble-hoz ezt még valahogy le kellene redukálni egy véges halmazra, lényegében egy rácsra. A Dobble esetében ez a rács 7×7-es lesz, ezért hívjuk a Dobble mögött álló geometriai rendszert hetedrendű véges projektív síknak. A további részletek szemléletesen benne vannak például a könyvben, ahogyan az is, hogy ha van otthon egy Dobble-paklid, hogyan tudod kirakni a kártyákat egy projektív rácsba.

104. feladvány: Dobble a köbön

A Dobble-pakli olyan kártyapakli, amelynek bármely két lapja között pontosan egy közös szimbólum van. Ha egy ilyen tulajdonsággal rendelkező paklit szeretnénk készíteni, akkor két triviális megoldás is adódik. Az egyik az, ha minden lapra ugyanazt a szimbólumot rakjuk, ekkor bármely kettő között lesz közös, csak kicsit egyszerű lesz megtalálni. Betehetünk persze egy csomó töltelék szimbólumot, amik csak egyszer szerepelnek, de akkor is unalmas lesz a játék, mert mindig ugyanazt kell bemondani.

Egy másik kézenfekvő lehetőség, ha bármely párra külön szimbólumot vezetünk be. Ha mondjuk van N = 20 lap, akkor N·(N-1)/2 = 190 párt lehet alkotni, ennyi szimbólum kell összesen, és egy kártya 19 másikkal lehet párban, tehát legalább 19 szimbólum kell egy kártyára, ami kicsit sok, átláthatatlan, és kissé gazdaságtalanul is használnánk a szimbólumokat.

Ha tehát Dobble-t akarunk készíteni, akkor megkövetelünk egyfajta nem triviális homogenitást: szerepeljen minden kártyán azonos számú szimbólum, a kártyákon semmi ne szerepeljen duplán, egy szimbólum ne csak egy párban szerepeljen, de ne is szerepeljen az összes lapon, sőt minden szimbólum ugyanannyi példányban legyen jelen.

A feladat most ugyanez lesz, de nem hagyományos Dobble-t szeretnénk készíteni, hanem kiterjesztjük a dolgot triókra. Egy olyan paklit szeretnénk, hogy bármely három lap esetében legyen pontosan egy közös szimbólum! A játék során tehát mindig három lapot szeretnénk felcsapni, és azok között kell minél hamarabb megtalálni a közös szimbólumot. A homogenitási követelmények ugyanazok: legyen minden kártyán ugyanannyi szimbólum, a kártyákon semmi ne szerepeljen duplán, egyik szimbólum se szerepeljen az összes lapon, de ne is csak három lapon, és minden szimbólum ugyanannyi példányban legyen jelen az egész pakliban. Lehetséges ilyen kártyajátékot alkotni?

Nehézségi szint:

A megfejtéseket részletes magyarázattal együtt az eszventura@qubit.hu címre várjuk. A legértékesebb megoldást küldő versenyzők felkerülnek az Ész Ventura dicsőségfalára, közöttük és minden jó megoldást beküldő versenyző között év végén nyereményeket sorsolunk ki. Az e-mail subject mezőjében kérjük sorszámmal jelezni, hogy melyik feladvány megoldásáról van szó. Beküldési határidő: december 10. éjfél.

Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus és bűvész.