Egy matematikai tétel, amely még a magyar politikát is megérintette. Egy tétel, amely majd másfél évszázadon át csak sejtés volt, pontosabban néha tétel, néha sejtés. Egy sejtés, amit Anglia térképe ihletett. Egy bizonyítás, aminek jelentős részét nem papírra írták és nem ember írta oda. Egy bizonyítás, amit élő ember nem tudott ellenőrizni. Talán már kitalálta a kedves olvasó. Igen, a négyszín-tételről van szó.

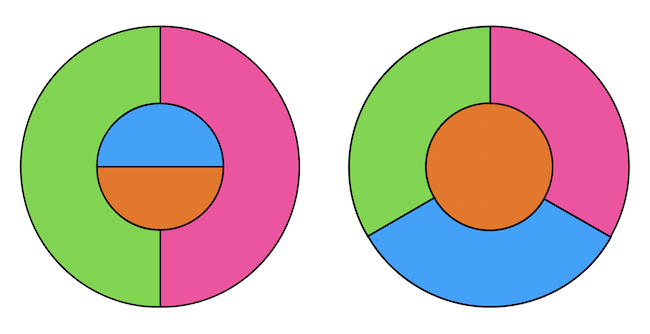
A négyszín-tétel azt állítja, hogy egy régiókra osztott síkot, például egy feltöredezett járdát, ki tudnak úgy színezni a Kétfarkú Kutyapárt aktivistái, hogy ne legyen két azonos színű (él)szomszédos régió, és ehhez elég legfeljebb négy szín. Az egészen nyilvánvaló, hogy három szín kevésnek bizonyulhat, lásd az alábbi minimál példákat. Azt pedig gráfelméleti alapokon nem túl nehéz megmutatni, hogy öt szín már biztosan elégséges a színezéshez (ötszín-tétel). Az viszont, hogy négy szín is elegendő, egészen sokáig csak sejtés volt.

Volt egy kutató, akit lenyűgöztek ezek a színtételek, és ebből szeretett volna társasjátékot csinálni, végül kutatói pályafutását feladva ma már csak társasjáték-tervezéssel foglalkozik. Adrian Adamescu nagy ötlete az volt, hogy színes dobókockákat használ, amiket úgy kell egymás mellé helyezni mintázatba, hogy ne csak azonos színek, de felső oldalukat tekintve azonos számok se kerüljenek egymás mellé. Ebből született meg a barcelonai Szent Család-templom, a Sagrada Família gyönyörű színes üvegablakait megidéző társasjáték. A Sagrada játék olyannyira sikeres lett, hogy a Kickstarteren kitűzött 24.000 dolláros célt a közösség ötszörösen finanszírozta meg, és azóta már magyar nyelven is elérhető a Reflexshop jóvoltából.

Mielőtt azonban a játékról írnék, egy picit kanyarodjunk még vissza a négyszín-tétel történetéhez – ha netán valaki nem ismeri –, hiszen számos érdekesség övezi. Kezdjük azzal, hogy 1852-ben Francis Guthrie valamilyen okból Anglia megyéit színezte, amikor észrevette, hogy ehhez négy színnél nem kell több. A megfogalmazott sejtést elmondta öccsének, aki elmondta tanárának, aki írt a kor egyik zsenijének, bizonyos Hamiltonnak, aki csak annyit mondott, hogy őt egyáltalán nem érdekli a kérdés. Igen, arról a Sir William Rowan Hamilton ír matematikusról, fizikusról és csillagászról van szó, akinek a gráfelméletben is több minden őrzi a nevét, például a Hamilton-kör, mert 1859-ben olyan játékot hozott forgalomba, amelyben egy gráf csúcspontjait kellett úgy bejárni, hogy minden csúcsot pontosan egyszer érintsünk – játékának állítólag nem volt átütő sikere. Ezen érdeklődését figyelembe véve fura, hogy nem érdekelte a kérdés, vagy legalábbis ezt állította.

Mindezek után számos sikertelen próbálkozás történt a sejtés bizonyítására. 1879-ben Alfred Kempe, majd tőle függetlenül 1880-ban Peter Guthrie Taité hitte azt, hogy bebizonyította a sejtést, de tíz évre rá kiderült, hogy mindkét bizonyításban volt hiba. 1890-ben viszont Percy Heawood, aki Kempe bizonyításában megtalálta a hibát, fel tudta használni Kempe eredményeit ahhoz, hogy bebizonyítsa legalább a kicsit gyengébb ötszín-tételt.

Végül hosszú előzmények után, rengeteg korábbi részeredményt felhasználva 1977-ben született meg egy minden korábbi matematikai bizonyításnál furcsább bizonyítás. Kenneth Appel és Wolfgang Haken a végtelen számú lehetséges térképet összesen 1936 elrendezésre redukálták, amiket egyenként számítógéppel ellenőrizni lehetett, így aztán a több ezer diagramot tartalmazó leírás mellett a bizonyítás része volt még 400 mikrokártya, ami a főszövegben levő tét tucatnyi lemma ezernyi eseteinek egyedi igazolását tartalmazta, és a bizonyítás részének tekinthető számítógépes program ezerkétszáz órán keresztül futott. Azóta egyébként már közöltek olyan bizonyítást is más témában, ami 200 terabájtos, így ez egyáltalán nem számít már rekordnak.

Mindezek után felmerül, hogy nincs-e hiba a bizonyításban. Volt is benne bőven. Több száz oldalnyi kézzel írott részt Haken tinédzser fia, Lippold segített ellenőrzni, de a publikálás után olyan nagy mennyiségű – bár javítható – hibát találtak még, hogy egyesek már nem is Appelt és Hakent tekintik a négyszín-tétel első bizonyítóinak. A megoldást mindenesetre azóta több ponton is egyszerűsítették, de ma sem olyan komplexitású, hogy ne lenne szükség számítógépre, és ember le tudná ellenőrizni. Ami megnyugtató lehet még, hogy 2004-ben sikerült a bizonyítás formális leírását a Coq tételbizonyító rendszerbe implementálni, és így már nem kell különböző számítógépes programokban megbízni, csak a sokak által már használt Coq tételbizonyítóban.

Ha viszont el is fogadjuk, hogy a rendszer hibátlanul működik, felvetődik a kérdés, hogy ez tényleg olyan matematika-e, amilyet szeretnénk? Egy tétel bizonyításának célja kettős. Az egyik kétségkívül a tétel igazságának bizonyítása, a másik egyáltalán nem lebecsülendő dolog viszont az, hogy mi emberek jobban megértsük a matematika működését, és ez utóbbihoz a program nem sokat tesz hozzá. Egy biztos: ez nem a nagybetűs Könyvből származó bizonyítás, ahogy Erdős Pál fogalmazna.

No és a játék?

A játékban alapvetően egy 4×5-ös négyzetrácsot (ablakot) kell betölteni színes kockákkal, mégpedig úgy, amint azt már említettük, hogy azonos színek és azonos számok se kerüljenek egymás mellé. Egy négyzetrács sakktáblaszerűen akár két színnel is színezhető volna, a játék mégis ötféle színű dobókockát használ, vannak ugyanis még az említetteken kívül más korlátozó tényezők is, amik nehezítik majd a játékosok dolgát. A játék léte tehát nem a négyszín-tételen áll vagy bukik, de az inspiráció mindenképpen onnan érkezett.

A játék végén a 4×5-ös négyzetrácson kialakuló mintázatokért különféle pontok kaphatók. Hogy mi ér pontot, az minden játékban más és más, mert három véletlenszerűen húzott kártya alakítja, ezek közös célok mindenkinek. Ilyen pontozható kombináció lehet például egy csupa különböző színből álló oszlop, vagy csupa különböző számból álló sor, vagy egyszínű átlós vonalak, stb. Ezen kívül mindenkinek van egy titkos saját színe: ennek a színnek a dobókockái önmagukban is pontot érnek a saját táblán, mindegyik annyit, ahány pöttye van felül.

A játék különlegessége még, hogy mindenki saját alapmintázatot kap az ablakához a játék elején, amiben bizonyos korlátozások szerepelnek, például hogy adott helyre csak adott szín vagy adott szám kerülhet. Ezáltal aszimmetrikus lesz a játék, de ez szükséges is, hogy ne ugyanaz legyen a két játékos stratégiája, hiszen leválogatással egy közös készletből jutnak majd hozzá a beépíthető dobókockákhoz. Ez az aszimmetria ugyanakkor nem okoz egyensúlytalanságot: bár az alapmintázatok eltérő nehézségűek, ezekből a játék elején választani lehet, és aki nehezebbet választ, az több támogatásra (üvegcseppre) számíthat a játék során; aki könnyebbet választ, az kevesebbre.

Támogatáshoz úgy lehet jutni, hogy az üvegcseppjeinkből költünk eszközkártyákra. Érdekes megoldás, hogy aki elsőként használ egy támogatást, az kevesebbet fizet érte, később már többet, de akárki akármelyiket használhatja, ha meg tudja még fizetni, körönként maximum egyet. Ilyen megvásárolható segítség lehet például, hogy egy-egy kockát utólag áthelyezünk, vagy az értékét eggyel megváltoztatjuk, és még sokféle más, de ezekből is hármat húzunk a játék elején, így minden játékban mások lesznek az elérhető potenciális segítségek.

Amiről nem beszéltünk még, hogy miként jutunk kockához. Zsákból húzzuk őket, majd dobunk velük, és anélkül, hogy forgatnák a kockákat, sorban választanak a játékosok. Valójában minden körben két kockák választhat mindenki, ennek megvan a pontos menete, és eggyel több kockát húzunk a zsákból, így még az utolsó kocka választása sem determinált. A játék tíz fordulón keresztül tart; ennyi elég ahhoz, hogy minden pozíciót betöltsünk az ablakunkon, és ha marad üres hely, az mínusz pontot fog érni.

A játék alkatrészei gyönyörűek. Kártyából viszonylag kevés van, ezért azokat könnyen lehet kártyavédőzni, és minden alkatrésznek szépen meg is van a helye a dobozban. A Sagrada újrajátszhatósága nagy, hiszen minden játék más, amit te magad is alakíthatsz a háttérminta kiválasztásával, de véletlenszerűen is változik a célkártyák és persze a húzott és dobott kockák által. Négy főig játszható, de két fővel is lényegében ugyanolyan jó: agyégető élmény. A kiadó 10 éves kortól ajánlja, de én akár már 8 éves kortól is ajánlanám. A játékhoz jelenleg angol nyelvű kiegészítő is elérhető, extra célokkal, extra lehetőségekkel, és néhány extra fehér színű kockával.

Ha absztrakt játékról van szó, gyönyörű színes kellékekkel zsákban, akkor mindenkinek rögtön eszébe juthat az Azul, amiről már mi is írtunk, az Év játéka volt 2018-ban. Ha valaki azon gondolkodik, hogy melyiket vegye meg, akkor talán érdemes összehasonlítanunk a kettőt, pontosabban itt beszélhetünk az egész Azul sorozatról is, mert most már megjelent a sorozat harmadik tagja is, az Azul – Királyi pavilon. Nekem személy szerint ez a harmadik a kedvencem az Azulok közül, mert a rombusz alakú elemek különlegesebbek, mint az eredetiben a négyzetek, és sokkal szabadabban lehet kombinálni benne néhány okos újítás miatt (jokerek, szobrok, tartalék kövek), de az összehasonlítás tekintetében nagyjából egy kalap alá vonhatók, mert az alap mechanika adja a játék leglényegét, ami mindegyikben ugyanaz.

Az Azulokban a közös mechanika a manufaktúrakorongról való különleges alapanyagszerzés (bővebben lásd korábbi cikkünket), amiben könnyen előfordulhat, hogy valaki nagyon jól jár, vagy nagyon rosszul, ütemtől függően, ezért az Azulokban kicsit több a harc az alapanyagokért. A mintázatokkal való kombinálás mindkét játék sajátja, de a Sagrada a különféle kártyákkal nagyobb újrajátszhatóságot tud, sőt más-más jellegű játékokat is eredményez (néha könnyebbet, néha nehezebbet), míg az Azulban a háttér és a célok elejétől fogva ismertek. Ennek ellenére mindkét játéknak megvan a szépsége; ha tehetitek, próbáljátok ki mindkettőt. Egy biztos: Sir William Rowan Hamilton játékánál mindenképpen jobb lett a Sagrada. Azt hiszem, ennél több is bizonyítható, de ezt egyelőre csak sejtésként fogalmazom meg.

A tesztpéldányt a Sagrada magyar nyelvű kiadója, a Reflexshop jóvoltából tesztelhettük, köszönjük!

Kapcsolódó cikkek a Qubiten: