Miért nem alkalmazható a Benford-törvény az amerikai választási körzetekre?
Hogyan szűrjük ki, ha egy adóbevallás fiktív számlaösszegeket tartalmaz, anélkül, hogy akár csak egy pillantást vetnénk a számlákra, vagy bármi fogalmunk lenne róla, mekkora összegű számlák lennének reálisak az adott cég működésében? Ha találunk statisztikai módszert a fiktív számlák lebuktatására, hasonló módszerrel egy választáson megjelenő esetleges fiktív szavazatokat is le lehet vajon leplezni? Az utóbbi kérdés nagy figyelmet kapott a közelmúltban, és érdeklődők sokasága kezdett ismerkedni a Benford-eloszlással.
A Benford-törvény gyakran segít az adóbevallásokkal kapcsolatos, lehetetlennek tűnő problémában, egy egyszerű és meglepő teszttel. A Frank Benford amerikai villamosmérnök és fizikus által 1938-ban leírt törvény azt mondja, hogy nagyon sok, a természetben előforduló adathalmaznál (és itt a természet részének tekinthetők a piaci mechanizmusok által generált számlák is) az első számjegyeknek valamilyen jól meghatározott gyakoriságot (az úgynevezett Benford-eloszlást) kell követniük. Mégpedig azon számok gyakorisága, ahol az első számjegy egyes, az összes adatnak körülbelül 30 százaléka, ahol kettes, az 18 százalék, és így tovább:
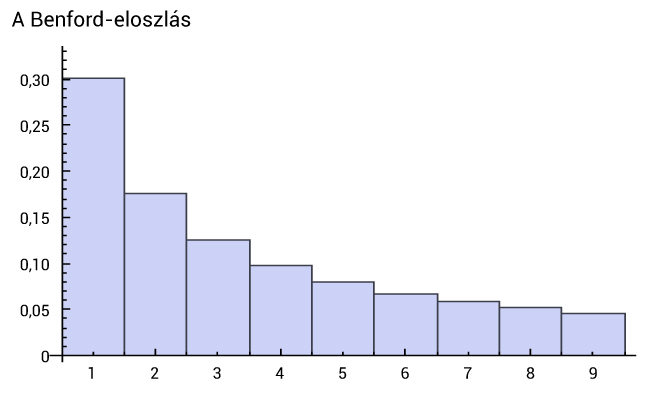
„De hiszen ez lehetetlen! Ha egy véletlen bevételi elemet kell hasraütésszerűen bemondanom, bármelyik számjegyet ugyanolyan eséllyel választom kezdő számjegynek! Miért lenne más ez a természet által generált véletlen számoknál?” –reagálnak sokan, amikor először hallanak a törvényről. Hogy milyen jelenség áll a Benford-törvény hátterében, azt hamarosan kifejtjük. Képzeletbeli vitapartnerünk pedig, aki hasraütéssel generált véletlen számokat, pont azzal bukna le, hogy az ő adatsorában nagyjából ugyanolyan eséllyel szerepelne mindegyik kezdő számjegy, míg egy cég valódi számlákból származó adatsorában a Benford-eloszlást látnánk. Ez a leleplező erő áll a Benford-eloszlás sikeres alkalmazásai mögött, amikor például adócsalások felderítésére szolgál. Az elv tehát: ha tudjuk, hogy az adatsornak a „természetben” Benford-eloszlást kellene követnie, és mégis nagyon eltér tőle, akkor nagy az esélye annak, hogy valaki manipulálta azt.
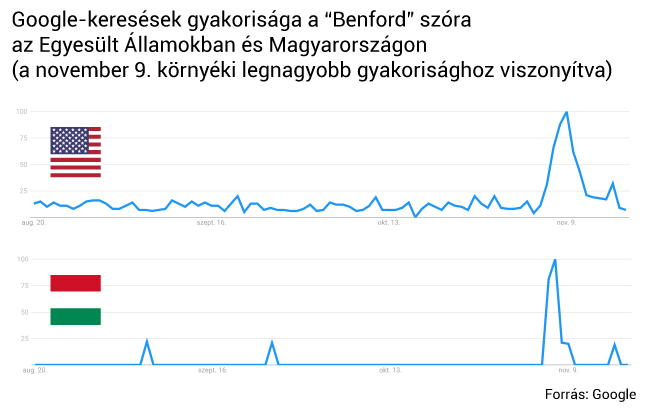
A 2020-as amerikai elnökválasztás a szélesebb közvélemény figyelmét is ráirányította a Benford-eloszlásra. Az interneten népszerűek lettek olyan grafikonok, amiken az látható, hogy némely csatatérállam választókörzeteiben a Trumpra leadott szavazatok követni látszanak a Benford-eloszlást, míg a Bidenre adott szavazatok nem (lásd például a 3. ábrát). Ebből többen azt a következtetést vonták le, hogy a Bidenre leadott szavazatokat utólag manipulálhatták. A megfigyelést a magyar sajtó egy része (Origo, Magyar Nemzet, Hír TV) is közölte, ezzel Magyarországot dobogós helyre repítve a „Benford” Google-keresések nemzetközi listáján.
Mi a Benford-eloszlás, és miért olyan gyakori (vagy ritka)?
Általában a természet számai között sokkal több kezdődne 1-essel mint 2-essel, ahogyan a Benford-törvény látszik állítani? Ez elsőre bizony teljes sületlenségnek tűnik. Például az ötjegyű számok közül ugyanúgy 10 000 darab kezdődik 1-essel, mint 2-essel, vagy bármilyen más számjeggyel. Ugyanilyen egyenlőség igaz nemcsak az ötjegyű számokra, hanem az 1, 2 vagy 1000 jegyű számokra is. A nem túl pontosan feltett kérdésre tehát határozott nemmel felelnénk.
De mi magyarázza akkor azt a jelenséget, amit Simon Newcomb már a XIX. században megfigyelt, hogy a logaritmustáblázatok köteteinek első lapjai sokkal jobban elkopnak, mint a későbbi lapok? (Azt az eshetőséget zárjuk ki, hogy sokan az elejétől elkezdték olvasni, de hamar elunták.) Ez más szavakkal azt jelenti, hogy a „valóságban előforduló” számok között jóval gyakoribbak az 1-es számjeggyel kezdődőek. Ezek a számok, amikkel a logaritmustábla használói találkoztak munkájuk során, akár generációkon keresztül, különböző szakterületek sajátos mennyiségei: könyvelésben szereplő számlák, pénzügyi vagy csillagászati megfigyelésekből származó adatok, stb. És valóban: az ilyen adathalmazok gyakran a 2. ábra szerinti gyakoriságokat mutatják.
Persze nem minden adathalmaz esetében várhatjuk a Benford-eloszlást: egy felnőtt ember magassága centiméterben kifejezve leggyakrabban 1-essel, sokkal ritkábban 2-essel fog kezdődni, és sohasem 3-assal. Az a tapasztalat, hogy a több nagyságrenden átívelő adathalmazokban látjuk ezt az eloszlást. Ha meg akarjuk érteni, hogy a Benford-törvénynek engedelmeskedő adathalmazokban az első számjegy miért követi ezt az eloszlást, először is kellene egy jó, matematikailag is megérthető modell, ami ilyen véletlen számokat generál. Így talán a jelenség mélyebb okához is intuíciót nyerhetünk.
A legegyszerűbb kiindulási pont az lenne, hogy tekintsünk egy véletlenszerűen választott pozitív egész számot úgy, hogy bármelyik szám kiválasztásának ugyanakkora legyen a valószínűsége. Hiszen miért szeretné jobban az univerzum az egyik számot a másiknál? Ennek azonban sajnos nincs értelme: a valószínűségek összege 1 kell, hogy legyen, ám végtelen sok egyenlő valószínűség összege nem lehet 1. Akkor közelítő megoldásként vehetnénk egyenlő valószínűségeket egy nagy, véges 1,2,...,N intervallumon. De egyrészt nem látszik, hogy létezne természetes választás N-re: 1 000 000? 6x10²³? Másrészt így különböző N értékekre lényegesen különböző eloszlásokat kapunk az első számjegyre, melyek közül egyik sem hasonlít a Benford-eloszláshoz.
Azt láttuk tehát, hogy egy véges számtani sorozat (mint az 1,2,3,...,6x10²³) véletlen eleme egyáltalán nem teljesítette a Benford-törvényt. De vegyünk most egy mértani sorozatot, mint amilyen például az 1,2,4,...,21000. Ha összeszámoljuk, az első számjegyek gyakoriságai egészen közel vannak a Benford által azonosítottakhoz.
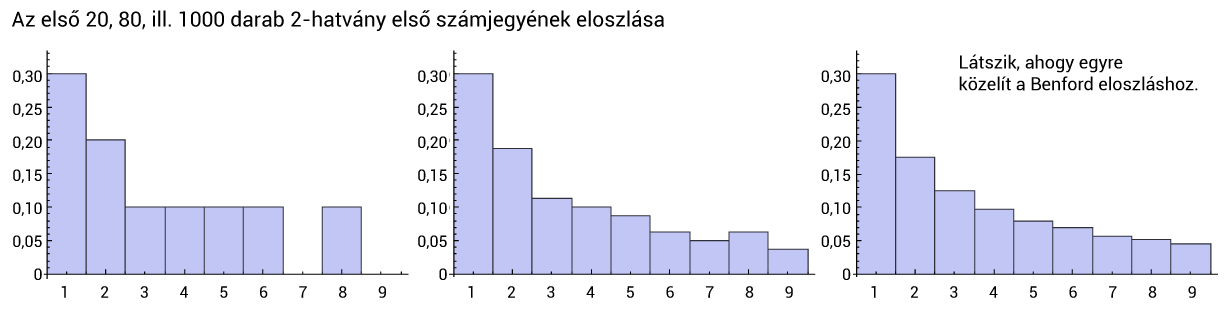
De vajon miből erednek a Benford által megfigyelt gyakoriságok: a 30,1 százalék, 17,6 százalék,...? A magyarázat elsőre ijesztőnek tűnhet.
Emlékeztetőül: egy pozitív x szám 10-es alapú logaritmusa az a kitevő, amire 10-et emelve x-et kapjuk. Például log 100=2 és log 0,1=-1. A logaritmus úgy kerül elő a Benford-eloszlásnál, hogy pontosan akkor lesz az x első számjegye a 10-es számrendszerben i, ha a log x törtrésze (amit úgy kapunk, hogy a tizedestört felírásában az tizedesvessző előtti részt 0-ra cseréljük) log (i+1) és log i között van. Mint a 2. ábránál jeleztük, 30.1% ≈ log 2 – log 1, ezután 17,6% ≈ log 3 – log 2, és hasonlóan, az i-edik számjegy Benford szerinti előfordulási sűrűsége éppen log10 (i+1) - log i. Tehát az, hogy egy nagy mintából véletlenül választott x szám teljesíti a Benford-törvényt, következne abból, ha a log x törtrésze nagyjából egyenletesen oszlana el a [0,1) intervallumon (azaz bármilyen részintervallumba az részintervallum hosszával nagyjából egyenlő valószínűséggel esne).
Ez jól magyarázza azt is, honnan jön a gyakran idézett feltétel, hogy az adatsorunk több nagyságrenden átívelő legyen: ha minden számunk például valami K és 5K között van, akkor a legkisebb és legnagyobb szám logaritmusa között is legfeljebb csak log 5 ≈ 0.7 a különbség, ami nyilván kizárja, hogy a teljes [0,1)-en egyenletesen oszoljanak el a törtrészek. Itt jegyezzük meg, hogy az említett egyenletes eloszlás tulajdonság miatt mindegy, hogy x-et milyen mértékegységben mérjük, vagyis skálafüggetlen, hiszen ha log x törtrésze egyenletes eloszlású a [0,1) intervallumon, akkor tetszőleges c>0 átváltási szorzó konstansra log cx = log c + log x törtrésze is egyenletes eloszlású, hiszen csak egy log c-vel való eltolásról van szó.
Minden olyan, a természetben vagy a társadalomban megfigyelt eset, ahol a Benford-törvény teljesül, valójában a fent részletezett, kicsit erősebb feltételt teljesíti: az egyes számok 10-es alapú logaritmusának törtrésze nagyjából egyenletesen helyezkedik el a [0,1)-en! Gondolhatunk erre úgy, mint a Benford-törvény valódi, bár kevésbé népszerű megfogalmazására.
Most már készen állunk arra, hogy megértsük, miért fordul elő a természetben a Benford-törvény. Rendkívül megnyugtató, hogy az imént megfogalmazott feltétel nem függ a választott számrendszertől (vagyis a megfigyelt jelenségek igazságtartalma nem múlik azon, hogy történetesen tíz ujjunk van), mint az a logaritmus azonosságainak felhasználásával könnyen bizonyítható. Ami még fontosabb, hogy ez az egyenletes eloszlás tulajdonság skálafüggetlen: nem számít, hogy milyen mértékegységet használunk. Sőt, könnyű bizonyítani, hogy a skálafüggetlenség nem csak konstans számmal való szorzásra teljesül, hanem akkor is, ha egy az adatsortól független véletlen számmal szorozzuk meg az adatsor elemeit. Például, ha az adatsorban szereplő mindegyik számhoz földobunk egy dobókockát, majd a számot megszorozzuk a dobás értékével, a keletkező új adatsor is teljesíti a törvényt, ha az eredeti teljesítette azt. Egy ennél erősebb tulajdonság is igaz: tegyük fel, hogy a kiindulási adatsorunk “nagyjából” (legfeljebb 2 százalékos hibával, mondjuk), teljesítette a Benford-törvényt. Ha most az előbbi módon független véletlen számokkal megszorozzuk az adatokat, akkor a keletkező új adatsor is teljesíti nagyjából a Benford-törvényt, ráadásul a hibaszázalék jó eséllyel csökken! Pont ez az abszorpciós tulajdonság (amit, mint bizonyítható, csak a Benford-eloszlás teljesít) magyarázhatja, hogy miért fordul elő olyan gyakran a természetben: ha független véletlen számokat szorozgatunk össze, a szorzat egyre inkább Benford-szerű viselkedést mutat.
Tehát, ha például az adathalmazunk elemei hosszú ideig exponenciális növekedésnek voltak kitéve, független véletlennek tekinthető hányadosokkal, mint például különböző termékek árai sok évi infláció hatására, nagyvárosok lélekszáma az urbanizáció hatására, vagy országok lakosságszáma, akkor a folyamat végeredménye reálisan kielégítheti a Benford-törvényt. Összegzésként elmondhatjuk, hogy az ilyen, egyfajta evolúció során kialakult mennyiségeknél várható a Benford-törvény megjelenése.
Térjünk vissza eredeti kérdésünkre. Vajon várható-e, hogy egy adott megye szavazóköreiben megjelent szavazók, vagy a közülük egy adott politikusra szavazók száma követi a Benford-törvényt? A rövid válasz az, hogy semmilyen indok nincsen erre. Egy megye összes szavazókörének létszáma nem hasonlítható (például) egy megye összes településének lélekszámához, hiszen előbbi nem spontán fejlődés, hanem emberi mérnökösködés eredménye, ráadásul pont azt szem előtt tartva, hogy minél egyenlőbbek legyenek ezek a számok, semmiképpen sem több nagyságrenden átívelőek. (Egyébként ha szavazókörzetek helyett egy adott állam egyes településein leadott szavazatok számát nézzük, ott már a Benford eloszlás megjelenését várnánk.)
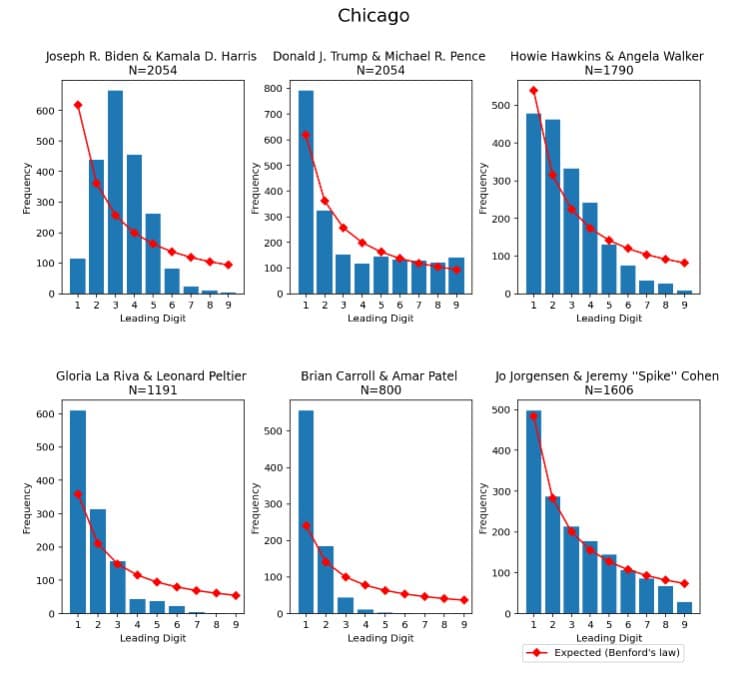
Ami mégis magyarázatot igényel, az az, hogy a 3. ábra alapján Trump és a kevésbé népszerű jelöltek adatai elég jól közelítik a Benford-eloszlást, míg Bidenéi látványosan eltérnek tőle. Leginkább szembeötlik, hogy minden más jelöltnél az 1 a leggyakrabban előforduló első számjegy (akárcsak a Benford-eloszlásnál), de Biden esetében ez kifejezetten ritka. A következőkben egy nagyvonalú számolással gyors és könnyen ellenőrizhető indoklást adunk.
A chicagói szavazókörzetek túlnyomó részébe 620 és 999 közötti számú választópolgár tartozik, és szinte mindenhol 65% fölötti részvétel volt jellemző (a levélszavazatokat is számolva). A körzetek nagyon nagy részében tehát összesen legalább 620x0.65=403 (és legfeljebb 999) szavazat érkezett be. Ahhoz tehát, hogy a valamely jelöltre leadott szavazatok száma 1-essel kezdődjön (ami csak akkor teljesülhet, ha 200 alá megy), szükségszerűen a voksok kevesebb, mint felét kellene megkapnia egy-egy ilyen körzetben.
Ezt a kihívást aránylag könnyen teljesítette Brian Carroll vagy Gloria La Riva. Viszont Biden esetében, aki elsöprő sikert aratott ezekben a hagyományosan erős demokrata körzetekben, szinte soha nem fordult elő a 200-nál kevesebb szavazat.
Persze aki a szavazatok manipulálására gyanakszik, az mondhatja, hogy az idei adatok, tehát a szavazatszámok, amikből dolgozunk, maguk is hamisak, legalábbis ami Bidenre érkezett és így ami az összes voksot illeti. Épp ezért folyamodtunk a fenti robusztus becsléshez, ami még akkor is igaz maradna, ha a Bidenre érkezett szavazatok egy nagyon jelentős hányadáról feltennénk, hogy hamis. Hiszen valójában a körzetek túlnyomó részében 75-85 százalékos eredménnyel nyert, így ha ezen voksok mondjuk negyedét kivennénk, a fenti gondolatmenet akkor is igaz lenne (vagyis: a bizonyítani próbált csalás nélkül számolt leadott voksok eleve nem teljesíthetik a Benford-törvényt).
Ami a Trump szavazatainál megfigyelhető viszonylagos illeszkedést illeti, itt is teljesen érthető az 1-esek és 2-esek nagy aránya: 4-800 szavazó 20-30 százaléka tipikusan 100 és 299 között lesz. Ráadásul figyeljük meg, hogy lényegesen nagyobb nála a 9-es gyakorisága, mint a 4-esé: ez a Benford-törvényre egyáltalán nem jellemző, míg a valóságban nem meglepő, ha több olyan körzet volt, ahol 100-nál éppen kevesebb szavazatot szerzett, mint olyan, ahol 400-nál is többet vagy 50-nél is kevesebbet.
A 3. ábra megfigyelésének legfőbb magyarázata tehát az, hogy bár a Benford-törvény teljesítését szavazóköri adatoktól nincs okunk elvárni, az előfordulhat, hogy adatsor véletlenül, történetesen teljesíti (néhány további hiba ismertetése megtalálható itt). Ez különösen így van, ha az adatsor számainak átlaga 10 és 20 vagy 100 és 200 közé esik, mint ez történt a Trumpra érkezett szavazatokkal. Míg ilyenkor “véletlenül” viszonylag közel leszünk a Benford-eloszláshoz, a jelenség oka nagyon távol van a Benford-törvény valódi mozgatórugójától, a nagyságrendeken átívelő számhalmaztól, amit egyfajta növekedési folyamat generált. De amikor a 3. ábrát csalás bizonyítékaként mutatták be egyes sajtótermékek, az olvasó már sejthette, hogy a kínált magyarázat nem állja meg a helyét - ha másból nem, hát abból, hogy a cikkek szerzői a téma egyetlen nevesített szakértőjét sem kérdezték meg.
A cikk szerzői: Pete Gábor, a Rényi Intézet tudományos főmunkatársa és a BME Sztochasztika Tanszék docense; Timár Ádám az Izlandi Egyetem kutatója és a Rényi Intézet tudományos főmunkatársa.
Kapcsolódó cikkek a Qubiten: