Mi a valószínűsége annak, hogy valaminek a valószínűsége nagyobb, mint valami? Pótkulcsok és a széf című feladványunkban egy ilyen kérdést tettünk fel, és sokan össze is zavarodtak tőle. A kérdés kulcsa természetesen az, hogy amikor egy bizonyos valószínűséget számolunk, miféle előzetes tudással rendelkezünk az adott dologról.

A feladat szerint egy folyosón 10 iroda található. Az irodákat már bezárták, és a dolgozók hazavitték magukkal a kulcsaikat. Viszont minden irodának van egy pótkulcsa, amit valamelyik másik irodában tartanak. Minden pótkulcs helyét véletlenszerűen választották ki, a többitől függetlenül, és egyforma valószínűséggel lehet a maradék 9 iroda bármelyikében. Egy irodában akár több kulcs is lehet. Ezen kívül az egyik irodában van egy széf, a széfnek pedig van egyetlen kulcsa, amit szintén egy másik irodában tartanak. A széf szintén egyforma valószínűséggel lehet bármelyik irodában, a kulcsa pedig ugyancsak egyforma valószínűséggel lehet a maradék 9 iroda bármelyikében.

Tegyük fel, hogy a tolvaj nyitva talál egy ajtót. A kérdés így hangzik:

Mi a valószínűsége annak, hogy úgy vannak az irodai pótkulcsok kiosztva, hogy a tolvaj akármelyik ajtót is találja nyitva, ezzel a bizonytalansággal együtt több mint 82 százalék esélye lesz arra, hogy ki tudja üríteni a széfet?

Vegyük észre, hogy a feladatban csupán az irodai pótkulcsok bizonyos típusú kiosztásának valószínűségére kérdeztünk rá, és a szóban forgó kiosztás nem tartalmazza a széf és a széf kulcsának a helyét. A lényeg tehát az ebben a feladatban, hogy bár a tolvaj érkezése előtt az irodai pótkulcsok, a széf és a széf kulcsa is mind megtalálható konkrétan valahol, attól függetlenül, hogy a tolvaj számára egyik hely sem ismert, mi most mégis mesterségesen szétválasztjuk a helyzet leírását, és azt a kérdést tesszük fel, hogy mekkora valószínűséggel olyan az irodai pótkulcsok kiosztása, hogy ezek után a széfnek és kulcsának kiosztása a már rögzített szituációban 82 százaléknál nagyobb esélyt ad a széf kiürítésére, akármelyik ajtót is találja nyitva a tolvaj.

Most nézzük meg, lehetséges-e, hogy 82 százaléknál nagyobb legyen a fenti valószínűség abban az esetben, ha van legalább két olyan szoba, amiben nincsen pótkulcs. Ha a tolvaj egy ilyen szobát találna nyitva (ennek egyenként 10 százalék a valószínűsége), akkor nem tudna továbbmenni sehova, így a széfet sem tudná kinyitni, mert a széf és annak kulcsa két külön szobában vannak. Így tehát együttesen legalább 20 százalékos a kudarc esélye a tolvaj szempontjából, vagyis 82 százaléknál kisebb a siker, ezért legfeljebb egy szoba lehet, amiben nincs pótkulcs az általunk keresett pótkulcs-kiosztásoknál.

Ha viszont legfeljebb egy kivételtől eltekintve minden szobában van pótkulcs, az azt jelenti, hogy attól a legfeljebb egy kivételtől eltekintve minden szobából tovább tudunk menni. Mivel pedig mindig tovább tudunk menni a szobában található pótkulccsal, egy idő után visszaérkezünk a kiindulási szobába. A szobák tehát klikkekbe rendeződnek, és az egy klikkbe tartozó szobák bármelyikéből elérhető a többi, legfeljebb egy különálló szoba lehet, ami valamelyik klikkből elérhető, de nincs benne pótkulcs.

Nézzük meg, lehetséges-e, hogy két klikkbe rendeződjenek a szobák. Ha a tolvaj ki tudja rámolni a széfet, az csak úgy lehet, ha a széf és a kulcsa is ugyanabba a klikkbe esik. Ha mondjuk van egy 2-es és egy 8-as klikk, akkor két eset lehetséges: vagy a kettes klikk egyik szobájába érkezik a tolvaj (20 százalék az esélye), vagy a 8-as klikkbe (80 százalék az esélye). Annak az esélye, hogy a széf is ugyanabba a klikkbe esik, mint ahova a tolvaj érkezik: (2/10)·(2/10) + (8/10)·(8/10) = 68 százalék – ez túl kevés, és azt még nem is néztük, hogy a széf kulcsa hol van, pedig még az is egy korlátozó tényező. Mármost könnyen belátható, hogy ha a klikkek méretei hasonlóbbak, vagy több klikk van, vagy bevesszük még a klikken kívül álló legfeljebb egy szobát, akkor ez a valószínűség csak csökken. Azt kapjuk tehát, hogy csakis egy klikk lehetséges, ha 82 százaléknál nagyobb valószínűséget szeretnénk.

Ha pedig egy klikk van, akkor az vagy 10-es, azaz minden szoba benne van, vagy pedig 9-es és egy szoba van külön, de a klikkből az is elérhető, csak pótkulcs nincs benne. Mindkét eset jó megoldás, mert az első esetben minden mindenhonnan elérhető, tehát a siker a tolvaj számára 100 százalékos, míg a második esetben csak akkor vall kudarcot a tolvaj, ha a különálló szobát találja nyitva. Minden más esetben szintén mindent elér, tehát a siker 90 százalékos ennél az esetnél. Most már csak össze kell számolnunk, hogy hányféle pótkulcskiosztás valósítja meg ezeket a szituációkat.

Nézzük előbb azt, hogy hány eset van, amikor az irodák kulcsai úgy vannak kiosztva, hogy azok körbenyitják az összes szobát, ahogy például az alábbi ábrán is látszódik. Ha egy szobában van kulcs, akkor onnan húzunk egy nyilat abba a szobába, amely szobát nyitja a szóban forgó kulcs. Így összesen tíz nyilat rajzolunk az ábrára, mégpedig úgy, hogy minden szobába kötelezően kell nyílnak mutatnia. A kérdés az, hogy mi a valószínűsége annak, hogy a nyilakat követve az összes szobán keresztül tudunk menni, azaz egy irányított – minden szobát magába foglaló – körút alakul ki a nyilak mentén.

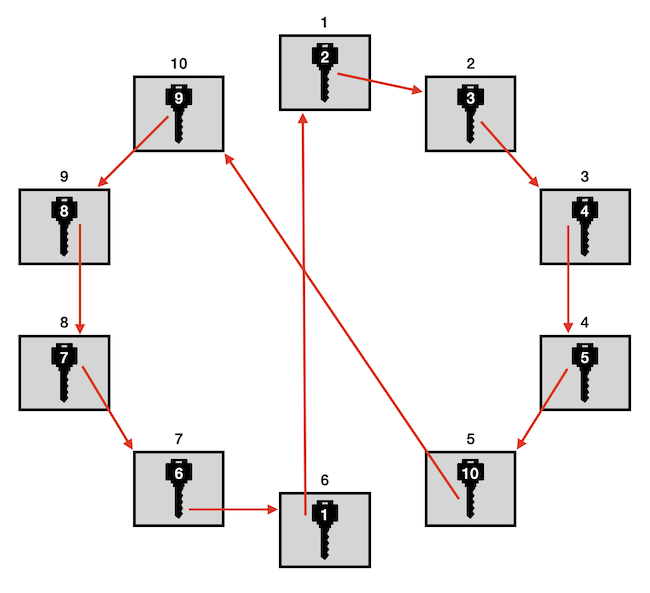
Nézzük meg, hány ilyen különböző konstelláció lehetséges. Vegyük az első szobának a kulcsát, az 9 féle helyen lehet. A fenti esetben ez például a 6-os szobában van. Ezután nézzük meg, hogy hol van annak a szobának a kulcsa, amely szobában az 1-es kulcsa van. A fenti esetben tehát a 6-os szoba kulcsáról van szó, ez 8 féle helyen lehet, ha körutat szeretnénk, mert az 1-es szobát ki kell zárnunk, hiszen ha ott lenne a 6-os kulcsa, akkor idő előtt záródna a körút. Ahogy így haladunk visszafelé, egyre csökken a lehetséges szobák száma, ahol az előző szoba kulcsa lehet, figyelembe véve azt, hogy a körút csak a legvégén záródhat be. Végeredményben azt kapjuk, hogy különböző körútak száma 9·7·6·5·4·3·2·1, amit 9! (ejtsd: kilenc faktoriális) módon rövidítünk.

Most nézzük meg, hányféleképpen állhat elő, hogy kilenc szoba rendeződik körútba, és egy szoba külön áll. A külön álló szoba 10 féle lehet, és annak a kulcsa 9 helyen lehet, a többi 9 szoba viszont 8! képpen rendeződhet körútba, ahogyan azt előzőleg láttuk, összességében tehát 10·9·8! = 10! ezen esetek száma.

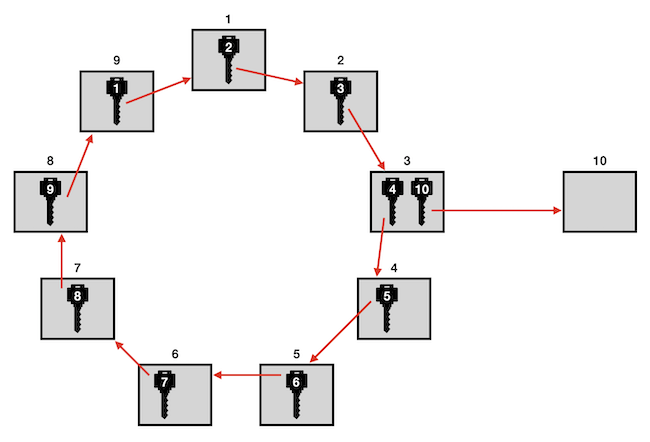
Az összes lehetséges kulcskiosztás pedig 9¹⁰, tehát a keresett valószínűség (9!+10!)/(9¹⁰), ami kb. egy ezrelék.

A legelső megoldó és a megoldásokért kiosztott banánok megtalálhatók a Dicsőségfalon!

Kapcsolódó cikk a Qubiten: