156. feladványunkban az volt a kérdés, hogy mi annak a valószínűsége, hogy egy adott héten az ötöslottó nyerőszámai közül a legkisebb nagyobb, mint hatoslottó nyerőszámai közül a legnagyobb.

Legyen H egy 6-nál nem kisebb és 45-nél nem nagyobb egész szám, így lehet a hatoslottó nyerőszámai közül a legnagyobb, mert a hatoslottón az 1-től 45-ig terjedő egész számokból húznak ki hat különböző számot. Nézzük hány olyan eset (számhatos) lehetséges, amikor H a legnagyobb a hatoslottó nyerőszámai közül. Ehhez H mellé 5 darab H-nál kisebb számot kell választani a pozitív egész számok közül, ennek jelölésére a Binomial(H-1,5) = (H-1)·(H-2)·(H-3)·(H-4)·(H-5)/5! jelölést (binomiális együtthatók) használjuk, ahol 5! = 5·4·3·2·1 az ún. faktoriális jele.

Most nézzük meg, hogy hány olyan eset (számötös) lehetséges, amikor teljesül, hogy az ötöslottó nyerőszámai H-nál nagyobbak. Ekkor 90-H darab számból kell választanunk öt számot, tehát a fenti jelöléssel Binomial(90-H,5) = (90-H)·(90-H-1)·(90-H-2)·(90-H-3)·(90-H-4)/5! lesz a kedvező esetek száma.

Ha az összes lehetséges kedvező kimenetelt szeretnénk összeszámolni, azaz az olyan számhatos és számötös lottóhúzáspárokat, amelyekre teljesül a feladat feltétele, akkor adott H esetén a lehetséges kedvező számötösök számát össze kell szoroznunk a lehetséges kedvező számhatosok számával, mert mindegyik párosítás egy megfelelő esetet szolgáltat, majd ezeket összegeznünk kell a lehetséges H értékekre 6-tól 45-ig. Tömören ezt az alábbi módon írhatjuk, és a WolframAlpha-ba ezt bemásolva:

"sum Binomial(H-1,5)*Binomial(90-H,5) H = 6 to 45"

rögtön ki is számolja nekünk:

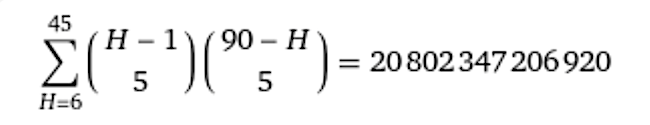
Ha pedig a valószínűségre vagyunk kíváncsiak, akkor ezt csak le kell osztanunk az összes lehetséges lottóhúzás párok számával, mert minden különböző húzáskombinációnak azonos a valószínűsége. Az ötöslottón Binomial(90,5) = 43949268 különböző húzás lehetséges, a hatoslottón Binomial(45,6) = 8145060, a különböző lottóhúzás párok összes száma pedig e kettőnek a szorzata, ami 357969424816080. A végeredmény tehát 20802347206920/357969424816080 = 4233/72842 = 0,058112, azaz majdnem 6%.

Kapcsolódó cikk a Qubiten: